要求尽可能地小
有4个不同的自然数,它们当中任意两个数的和是2的倍数,任意三个数的和都是3的倍数。为了使这4个数尽可能地小,这4个数的和是多少?分析与解 要满足“任意两个数的和都是2的倍数”这个条件,这4个数的奇偶性必须相同,要么都是奇数,要么都是偶数。要满足“任意三个数的和是3的倍数”这个条件,要求这4个数中的每个数要么都是3的倍数,要么都是被3除余1的数,要么都是被3除余2的数。但又要求“这4个数尽可能地小”,经试验,只有每个数都是被3除余1的数才行。所以,这4个数为:1、7、13、19这4个数的和是:1+7+13+19=40
教育新鲜事
 七根铁链
七根铁链 14÷2≠7吗?
14÷2≠7吗?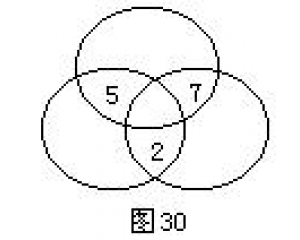 空白处填几?
空白处填几?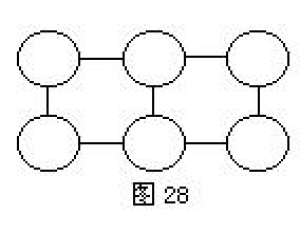 中间的两个圆圈里该填几
中间的两个圆圈里该填几