小龙买早点
一天,小龙带若干钱上街买早点。如果他买尽可能多的大饼(每只3分),要剩下1分钱;如果买尽可能多的油条(每根4分),也要剩1分钱。他至少带了多少钱?又有一天,小龙带若干钱上街买早点。如果买尽可能多的大饼,要多 2分钱;买尽可能多的油条,要多3分钱,问这一天他至少带了多少钱?
答案:第一天,小龙如果把多带的1分钱藏起来,那么他全买大饼就可以把钱用“完”,全买油条也可以把钱用“完”。他带的钱减去1之后,是3和4的最小公倍数12,所以他带的钱是12+1=13(分),即一角三分。第二天,小龙如果能“借”到1分饯,那么全买大饼或全买油条都可以把钱用完。他带的钱加上1之后,是3和4的最小公倍数12,所以他带的钱是12-1=11(分),即一角一分。下面,我们用一种新的方法来讨论:
图片1
图片1
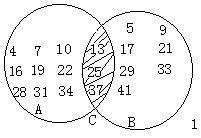
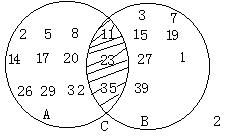
把A与B这两个圆圈交叉,形成一个公共部分C(上图),这里面的数既有“除以3余数为1”的性质,又有“除以4余数为1”的性质,就是我们要找的那种“全买大饼多1分,都买油条也多1分”的数,而题目问“至少带了多少钱”,即应找出C这个部分的数里面最小的一个,即13,所以小龙这天带了一角三分钱上街。对于第二天的情况,可以完全类似地讨论,我们不再重复,但为你画好了一张图(下图),你自己进行解释吧!请注意:具有某种相同属性的事物的总称,叫“集合”。比如我们第一次写在圆圈A里的数的总称即“除以3余数为1的数的集合”。
答案:第一天,小龙如果把多带的1分钱藏起来,那么他全买大饼就可以把钱用“完”,全买油条也可以把钱用“完”。他带的钱减去1之后,是3和4的最小公倍数12,所以他带的钱是12+1=13(分),即一角三分。第二天,小龙如果能“借”到1分饯,那么全买大饼或全买油条都可以把钱用完。他带的钱加上1之后,是3和4的最小公倍数12,所以他带的钱是12-1=11(分),即一角一分。下面,我们用一种新的方法来讨论:

图片1

图片1
把A与B这两个圆圈交叉,形成一个公共部分C(上图),这里面的数既有“除以3余数为1”的性质,又有“除以4余数为1”的性质,就是我们要找的那种“全买大饼多1分,都买油条也多1分”的数,而题目问“至少带了多少钱”,即应找出C这个部分的数里面最小的一个,即13,所以小龙这天带了一角三分钱上街。对于第二天的情况,可以完全类似地讨论,我们不再重复,但为你画好了一张图(下图),你自己进行解释吧!请注意:具有某种相同属性的事物的总称,叫“集合”。比如我们第一次写在圆圈A里的数的总称即“除以3余数为1的数的集合”。
教育新鲜事
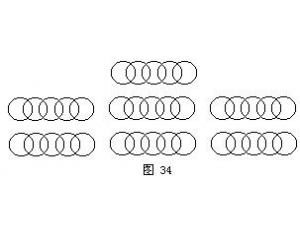 七根铁链
七根铁链 14÷2≠7吗?
14÷2≠7吗?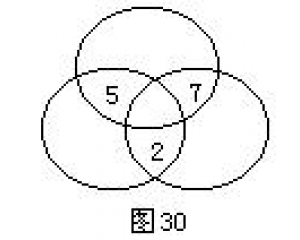 空白处填几?
空白处填几?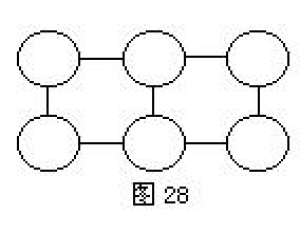 中间的两个圆圈里该填几
中间的两个圆圈里该填几