按要求组数
用0、1、2、3、7、8六个数字可以组成多少个能被9整除的、没有重复数字的四位数。
分析与解 能被9整除的数的特征是:“一个数各个数位上的数字和能被9整除,这个数就能被9整除。”在0、1、2、3、7、8这六个数字中,1、2、7、8与0、3、7、8这两组数字的数字和都是9的倍数。因此,用这两组数字组成的四位数必然能被 9整除。用1、2、7、8能组成24个四位数。用0、3、7、8能组成18个四位数。所以一共可以组成24+18=42(个)能被9整除、又没有重复数字的四位数。
分析与解 能被9整除的数的特征是:“一个数各个数位上的数字和能被9整除,这个数就能被9整除。”在0、1、2、3、7、8这六个数字中,1、2、7、8与0、3、7、8这两组数字的数字和都是9的倍数。因此,用这两组数字组成的四位数必然能被 9整除。用1、2、7、8能组成24个四位数。用0、3、7、8能组成18个四位数。所以一共可以组成24+18=42(个)能被9整除、又没有重复数字的四位数。
相关文章
教育新鲜事
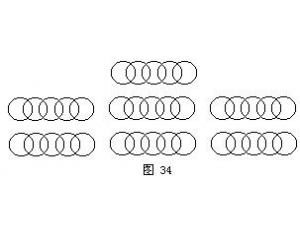 七根铁链
七根铁链 14÷2≠7吗?
14÷2≠7吗?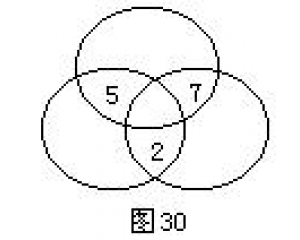 空白处填几?
空白处填几?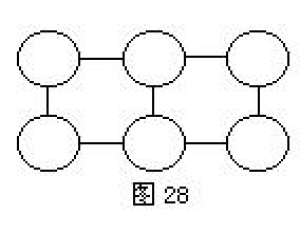 中间的两个圆圈里该填几
中间的两个圆圈里该填几