小学数学必考题型及口诀汇总,一遍就能记住!
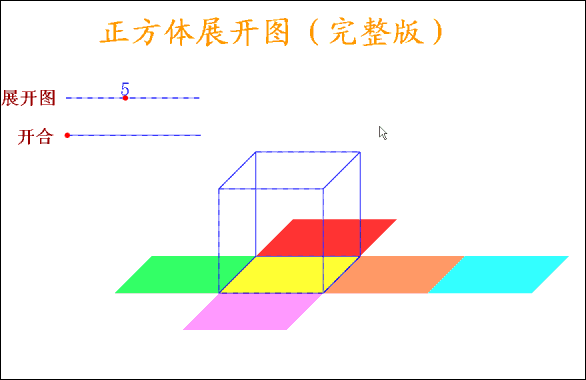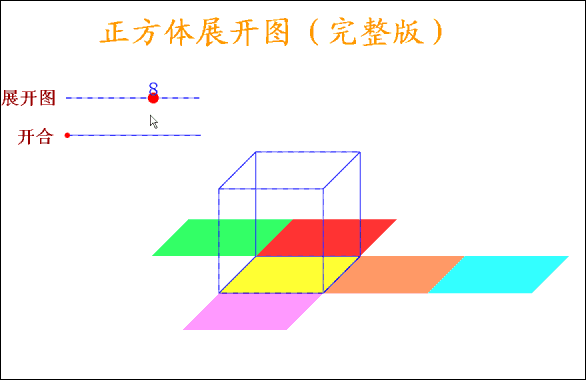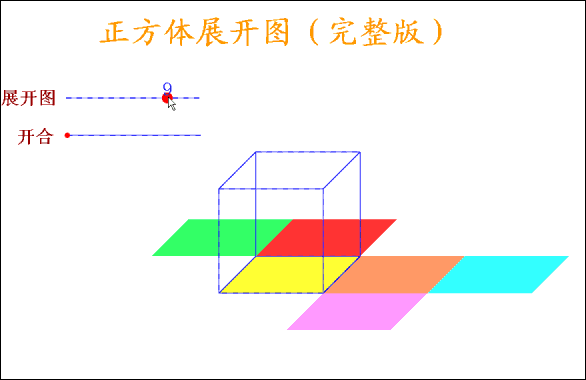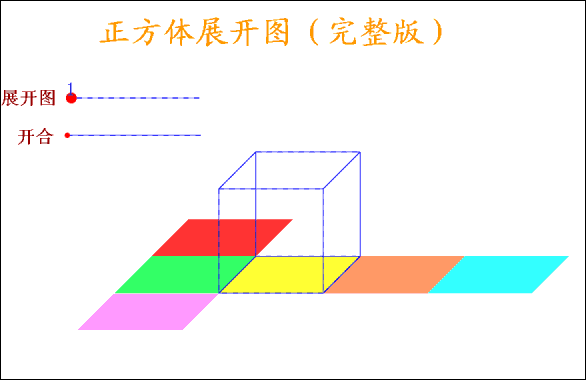
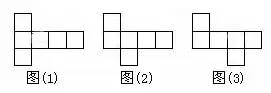
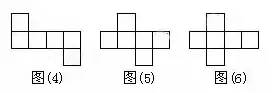
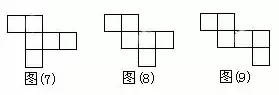
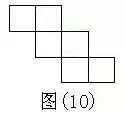
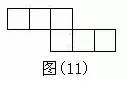
正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型: 按口诀,则大数=(10+2)/2=6,小数=(10-2)/2=4。 【口诀】: 求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24 (1)加水稀释 【口诀】: 加水先求糖,原来含糖为:20X15%=3(千克) 糖水减糖水,后的糖水量减去原来的糖水量, 30-20=10(千克) 【口诀】: 加糖先求水,原来含水为:20X(1-15%)=17(千克) 水完求糖水,含17千克水在20%浓度下应有多少糖水, 17/(1-20%)=21.25(千克) 糖水减糖水,后的糖水量减去原来的糖水量, 21.25-20=1.25(千克) (1)相遇问题 【口诀】: 相遇那一刻,路程全走过。即甲乙走过的路程和恰好是两地的距离120千米。 【口诀】: 先走的路程,为3X2=6(千米) 分母比数和,即分母为:2+3+4=9; 【口诀】: 先求一倍的量,12/(7-4)=4, 【口诀】: [1-(1/6+1/4)X2]/(1/6)=1(天) 【口诀】: 路是直的。所以植树120/4+1=31(棵)。 例2:在一条长为120米的圆形花坛边植树,间距为4米,植树多少棵? 路是圆的,所以植树120/4=30(棵)。 【口诀】: 一盈一亏,则公式为:(9+7)/(10-8)=8(人),相应桃子为8X10-9=71(个) 例2:士兵背子弹。每人45发则多680发;每人50发则多200发,多少士兵多少子弹? 全盈问题。大的减去小的,则公式为:(680-200)/(50-45)=96(人)则子弹为96X50+200=5000(发)。 例3:学生发书。每人10本则差90本;每人8 本则差8本,多少学生多少书? 全亏问题。大的减去小的。则公式为:(90-8)/(10-8)=41(人),相应书为41X10-90=320(本) 【口诀】: 每牛每天的吃草量假设是1,则27头牛6天的吃草量是27X6=162,23头牛9天的吃草量是23X9=207; 岁差不会变,今年的岁数差点34-8=26,到几年后仍然不会变。 例2:姐姐今年13岁,弟弟今年9岁,当姐弟俩岁数的和是40岁时,两人各应该是多少岁? 岁差不会变,今年的岁数差13-9=4几年后也不会改变。 【口诀】:
相关文章
- 小学数学11个计算技巧:提升孩子的计算能力!
- 小学数学概念+知识点顺口溜,考试不用愁!
- 小学数学做题宝典,加减法、乘法快速口诀表
- 小学数学一年级下册人民币单位换算100题(有答案)
- 小学数学 | 人民币换算计算方法,你家孩子掌握了吗?
- 小学数学不好?学习方法很重要!一定要告诉孩子
- 小学数学非常有效的“画图”解题法!家长快为孩子收藏
- 掌握这8类简算方法,小学数学简便计算再也不出错!
- 小学数学最强计算技巧总结!错过了太可惜~
- 小学数学考试中错误率较高的几种典型题
- 小学数学6类“画图”解题,快教给孩子
- 小学数学要想拿高分,必须攻克这13种典型题!赶紧为孩子收藏
- 小学数学一年级下册读数、写数练习题+应用题练习集锦,给孩子放
- 小学数学14个计算技巧:让孩子的计算能力爆表!
- 小学数学最容易出错的16个“小细节”,千万别在这上面丢分!
- 小学丨数学借用思维导图,学习简单的行程问题
- 小学数学所有公式和顺口溜都在这里了,拿走不谢!
- 这些小学数学基础知识顺口溜,让学生越读越爱学!
- 9大图形解法搞定小学数学几何易错题
- 小学数学单位换算公式大全及专项训练
推荐内容
教育新鲜事
 小学语文“选词填空”汇
小学语文“选词填空”汇 小学数学11个计算技巧:
小学数学11个计算技巧: 小学数学做题宝典,加减
小学数学做题宝典,加减 小学英语自然拼读法基本
小学英语自然拼读法基本