9大图形解法搞定小学数学几何易错题
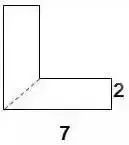
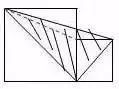
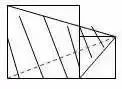
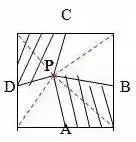
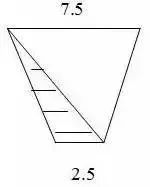
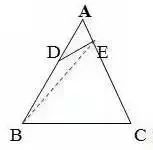
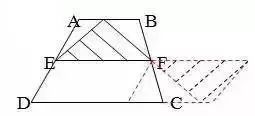
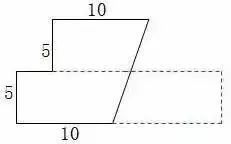
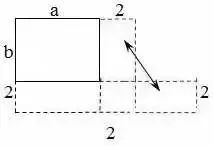
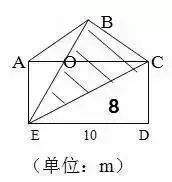
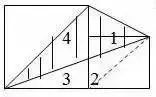
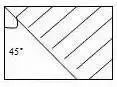
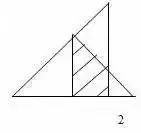
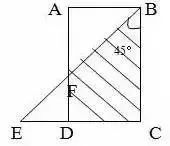
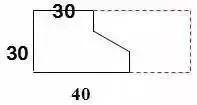
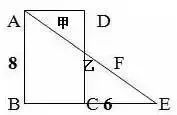
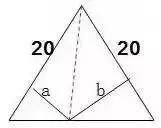
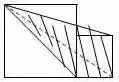
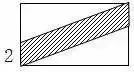
1.直线没有端点,没有长度,可以无限延伸。 2.射线只有一个端点,没有长度,射线可以无限延伸,并且射线有方向。 3.在一条直线上的一个点可以引出两条射线。 4.线段有两个端点,可以测量长度。圆的半径、直径都是线段。 5.角的两边是射线,角的大小与射线的长度没有关系,而是跟角的两边叉开的 大小有关,叉得越大角就越大。 6.几个易错的角边关系: (1)平角的两边是射线,平角不是直线。 (2)三角形、四边形中的角的两边是线段。 (3)圆心角的两边是线段。 7.两条直线相交成直角时,这两条直线叫做互相垂直。其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。 8.从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。 9.在同一个平面上不相交的两条直线叫做平行线。 1.任何三角形内角和都是180度。 2.三角形具有稳定的特性,三角形两边之和大于第三边,三角形两边之差小于第三边。 3.任何三角形都有三条高。 4.直角三角形两个锐角的和是90度。 5.两个三角形等底等高,则它们面积相等。 6.面积相等的两个三角形,形状不一定相同。 1. 正方形面积:边长×边长 2.正方形面积:两条对角线长度的积÷2 1. 两个完全一样的三角形能组成一个平行四边形。 2.两个完全一样的直角三角形能组成一个长方形。 3.两个完全一样的等腰直角三角形能组成一个正方形。 4.两个完全一样的梯形能组成一个平行四边形。 1.把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径。则长方形的面积等于圆的面积,长方形的周长比圆的周长增加r×2。 2.半圆的周长等于圆的周长的一半加直径。 3.半圆的周长公式:C=pd?2+d或C=pr+2r 4.在同一个圆里,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。而面积扩大或缩小以上倍数的平方倍。 1.把圆柱的侧面展开,得到一个长方形,这个长方形的长等于圆柱的底面的周长,宽等于圆柱的高。 2.如果把圆柱的侧面展开,得到一个正方形,那么圆柱的底面周长和高相等。 3.把一个圆柱沿着半径切开,拼成一个近似的长方体,体积不变,表面积增加了两个面,增加的面积是r×h×2。 4.把一个圆柱沿着底面直径劈开,得到两个半圆柱体,表面积和比原来增加了两个长方形的面,增加的面积和是d×h×2。 5.把一个圆柱加工成一个最大的圆锥,那么圆柱与圆锥等底等高,削去的圆柱的体积占圆柱体积的, 削去的圆柱的体积占圆锥体积的2倍。 6.把一个圆柱截成几段,增加的表面积是底面圆,增加的面的个数是:截的次数×2。 1.分割线法 ▌例1:将两个相等的长方形重合在一起,求组合图形的面积。(单位:厘米) 解:将图形分割成两个全等的梯形。S组=(7-2+7)×2÷2×2=24(平方厘米) ▌例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。 解:将图形分割成3个三角形。S=5×5÷2+5×8÷2+(8-5)×5÷2=12.5+20+7.5=38(平方厘米) ▌例3:左图中两个正方形边长分别为8厘米和6厘米。求阴影部分面积。 解:将阴影部分分割成两个三角形。 S阴=8×(8+6)÷2+8×6÷2=56+24=80(平方厘米) 2.添加辅助线法 ▌例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。求阴影部分面积。 解:从P点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。S阴=4×4÷2=8(平方厘米) ▌例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。梯形下底是多少厘米? 解:因为添一条辅助线平行于三角形一条边,发现40平方厘米是一个平行四边形。 所以梯形下底:40÷8=5(厘米) ▌例3:平行四边形的面积是48平方厘米,BC分别是这个平行四边形相邻两条边的中点,连接A、B、C得到4个三角形。求阴影部分的面积。 解:如果连接平行四边形各条边上的中点,可以看出空白部分占了整个平行四边形的八分之五,阴影部分占了八分之三。 S阴=48÷8×3=18(平方厘米) 3.倍比法 ▌例1:已知OC=2AO,SABO=2㎡,求梯形ABCD的面积。 解:因为OC=2AO,所以SBOC=2×2=4(㎡)SDOC=4×2=8(㎡) SABCD=2+4×2+8=18(㎡) ▌例2:已知S阴=8.75㎡,求下图梯形的面积。 解:因为7.5÷2.5=3(倍)所以S空=3S阴S=8.75×(3+1)=35(㎡) ▌例3:下图AB是AD的3倍,AC是AE的5倍,那么三角形ABC的面积是三角形ADE的多少倍? 解:设三角形ADE面积为1个单位。 则SABE=1×3=3 SABC=3×5=15 所以三角形ABC的面积是三角形ADE的15倍。 4.割补平移 ▌例1:已知S阴=20㎡,EF为中位线求梯形ABCD的面积。 解:沿着中位线分割平移,将原图转化成一个平行四边形。从图中看出,阴影部分面积是平行四边形面积一半的一半。SABCD=20×2×2=80(㎡) ▌例2:求下图面积(单位厘米)。 解1:S组=S平行四边形=10×(5+5)=100(平方厘米) 解2:S组=S平行四边形=S长方形=5×(10+10)=100(平方厘米) ▌例3:把一个长方形的长和宽分别增加2厘米,面积增加24平方厘米。求原长方形的周长。 解:C=(24÷2-2)×2=20(厘米) 5.等量代换 ▌例1:已知AB平行于EC,求阴影部分面积。 解:因为AB//EC所以S△AOE=S△BOC则S阴=0.5S长方形=10×8÷2=40(㎡) ▌例2:下图两个正方形边长分别是6分米、4分米。求阴影部分面积。 解:因为S1+S2=S3+S2=6×4÷2所以S1=S3 则S阴=6×6÷2=18(平方分米) 6.等腰直角三角形 ▌例1:已知长方形周长为22厘米,长7厘米,求阴影部分面积。 解:宽=22÷2-7=4(厘米)S阴=(7+(7-4))×4÷2=20(平方厘米) 或S阴=7×4-4×4÷2=20(平方厘米) ▌例2:已知下列两个等腰直角三角形,直角边分别是10厘米和6厘米。求阴影部分的面积。 解:10-6=4(厘米) 6-4=2(厘米)S阴=(6+2)×4÷2=16(厘米) ▌例3:下图长方形长9厘米,宽6厘米,求阴影部分面积。 解:三角形BCE是等腰三角形 FD=ED=9-6=3(厘米)S阴=(9+3)×6÷2=36(平方厘米) 或S阴=9×9÷2-3×3÷2=36(平方厘米) 7.扩倍法、缩倍法 ▌例:求左下图的面积(单位:米)。 解:将原图扩大两倍成长方形,求出长方形的面积后再缩小两倍,就是原图形面积。S=(40+30)×30÷2=1050(平方米) 8.代数法 ▌例1:图中三角形甲的面积比乙的面积少8平方厘米,AB=8cm,CE=6cm。求三角形甲和三角形乙的面积各是多少? 解:设AD长为Xcm。再设DF长为Ycm。 8X+8=8(6+X)÷2X=44Y÷2+8=6(8-Y)÷2Y=3.2 S甲=4×3.2÷2=6.4(c㎡) S乙=6.4+8=14.4(c㎡) ▌例2:下图是一个等腰三角形,它的腰长是20厘米,面积是144平方厘米。在底边上任取一点向两腰作垂线,得a和b,求a+b的和。 解:过顶点连接a、b的交点。 20b÷2+20a÷2=14410a+10b=144 a+b=14.4 9.看外高 ▌例1:下图两个正方形的边长分别是6厘米和3厘米,求阴影部分的面积。 解:从左上角向右下角添条辅助线,将S阴看成两个钝角三角形。(钝角三角形有两条外高) S阴=S△1+S△2 =3×(6+3)÷2+3×6÷2=22.5(平方厘米) ▌例2:下图长方形长10厘米,宽7厘米,求阴影部分面积。 解:阴影部分是一个平行四边形。与底边2厘米对应的高是10厘米。 S阴=10×2=20(平方厘米)


相关文章
- 小学数学11个计算技巧:提升孩子的计算能力!
- 小学数学概念+知识点顺口溜,考试不用愁!
- 小学数学做题宝典,加减法、乘法快速口诀表
- 小学数学一年级下册人民币单位换算100题(有答案)
- 小学数学 | 人民币换算计算方法,你家孩子掌握了吗?
- 小学数学不好?学习方法很重要!一定要告诉孩子
- 小学数学非常有效的“画图”解题法!家长快为孩子收藏
- 掌握这8类简算方法,小学数学简便计算再也不出错!
- 小学数学最强计算技巧总结!错过了太可惜~
- 小学数学考试中错误率较高的几种典型题
- 小学数学6类“画图”解题,快教给孩子
- 小学数学要想拿高分,必须攻克这13种典型题!赶紧为孩子收藏
- 小学数学一年级下册读数、写数练习题+应用题练习集锦,给孩子放
- 小学数学14个计算技巧:让孩子的计算能力爆表!
- 小学数学最容易出错的16个“小细节”,千万别在这上面丢分!
- 小学丨数学借用思维导图,学习简单的行程问题
- 小学数学所有公式和顺口溜都在这里了,拿走不谢!
- 这些小学数学基础知识顺口溜,让学生越读越爱学!
- 小学数学单位换算公式大全及专项训练
- 小学数学12个估算方法详解,省去验算时间!
推荐内容
教育新鲜事
 小学语文“选词填空”汇
小学语文“选词填空”汇 小学数学11个计算技巧:
小学数学11个计算技巧: 小学数学做题宝典,加减
小学数学做题宝典,加减 小学英语自然拼读法基本
小学英语自然拼读法基本