小学数学非常有效的“画图”解题法!家长快为孩子收藏
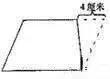
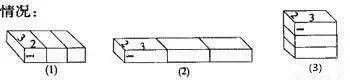
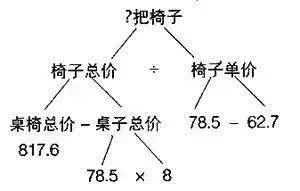
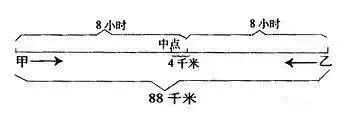
学过数学的人都知道,思维方式的运用在学习数学这一科目上的重要性,小学阶段的数学主要培养的是孩子的逻辑思维能力,是从形象思维逐步过度到抽象思维的过程,如果在小学阶段没有将基础打牢,那么等孩子上初中后面对更复杂的学习内容,就会变得更吃力。 可以这样说,审题是对题目进行初步的感知,特别是应用题,而理解题意这个环节,决定你考了问题的角度,确定你考虑问题的方法,因此,这是做题中的重要环节。 根据审题的内容画图,把该题的条件、问题在图上表明,借助线段图或实物图把抽象的数学问题具体化,还原本来的面目,从而找到解决问题的方法,从图中一下子就可以找到答案,而且通过画图也能很快找到自己的错误。 很多小学生做应用题,就知道看题目,草稿纸也不用,紧盯着啊看啊......能看出花来?光看题,又不是看小说。 借助画图帮助孩子理解题意 是至关重要的一步 借助画图解题,它是孩子打开解决问题大门的一把“金钥匙”,很多问题都可以很快速的求解,比如几何问题、路程问题,如果光靠想是很难想出答案的画图就一目了然,下面我们举几个栗子来看看。 1、平面图 对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题,可以借助画平面图帮助思考解题。 如,有两个自然数A和B,如果把A增加12,B不变,积就增加72;如果A不变,B增加12,积就增加120,求原来两数的积。 根据题目的条件比较抽象的特点,不妨借用长方形图,把条件转化为因数与积的关系。先画一个长方形,长表示A,宽表示B,这个长方形的面积就是原来两数的积。如图(l)所示。 根据条件把A增加12,则长延长12,B不变即宽不变,如图(2);同样A不变即长不变,B增加12,则宽延长12,如图(3)。从图中不难找出: 原长方形的长(A)是120÷12=10 原长方形的宽(B)是72÷12=6 则两数的积为10×6=60 借助长方形图,弄清了题中的条件,找到了解题的关键。 再如,一个梯形下底是上底的1.5倍,上底延长4厘米后,这个梯形就变成一个面积为60平方厘米的平行四边形。求原来梯形面积是多少平方厘米? 根据题意画平面图: 从图中可以看出:上、下底的差是4厘米,而这4厘米对应的正好是1.5-l=0.5倍。所以上底是4÷(1.5-1)=8(厘米),下底是8×1.5=12(厘米),高是60÷12=5(厘米),则原梯形的面积是(8+12)×5÷2=50(平方厘米)。 2、立体图 一些求积题,结合题目的内容画出立体图,这样做,使题目的内容直观、形象,有利于思考解题。 如,把一个正方体切成两个长方体,表面积就增加了8平方米。原来正方体的表面积是多少平方米? 如果只凭想象,做起来比较困难。按照题意画图,可以帮助我们思考,找出解决问题的方法来。按题意画立体图: 从图中不难看出,表面积增加了8平方米,实际上是增加 2个正方形的面,每个面的面积是8÷2=4(平方米)。原正方体是6个面,即表面积为4×6=24(平方米)。 再如,用3个长3厘米、宽2厘米、高1厘米的长方体,拼成一个大长方体。这个大长方体的表面积是多少? 按题意画立体图来表示,三个长方体拼成的大长方体有以下三种情况: (l)拼成长方体的长是2×3=6(厘米),宽3厘米,高1厘米。表面积为(6×3+6×1+3×1)×2=54(平方厘米)。 (2)拼成长方体的长是3×3=9(厘米),宽2厘米,高1厘米。表面积为(9×2+9×1+2×1)×2=58(平方厘米)。 (3)拼成长方体的长是3厘米,宽是2厘米,高是1×3=3(厘米)。表面积为(3×2+3×3+2×3)×2=42(平方厘米)。 这道题有以上三种答案,通过画图起到审题和理解题意的作用。 3、分析图 一些应用题,为了能正确审题和分析题目中的数量关系,可以把题目中的条件、问题的相互关系用分析图表示出来。 如,新华中学买来 8张桌子和几把椅子,共花了 817.6元。每张桌子价 78.5元,比每把椅子贵 62.7元,买来椅子多少把? 分析图: (l)买椅子共花多少钱? 817.6-78.5×8=189.6元) (2)每把椅子多少钱? 78.5-62.7=15.8(元) (3)买来椅子多少把?189.6÷15.8=12(把) 综合算式为: (817.6-78.5×8)÷(78.5-62.7) =189.6÷15.8 =12(把) 答:买来椅子12把。 4、线段图 一些题目条件多,条件之间关系复杂,一时难以解答。可画线段图表示,寻求解题的突破口。 如,光明小学六年级毕业生比全校总人数的还多30人。新学期一年级新生人学360人,这样现在比原全校总人数增加了。求原来全校学生有多少人? 从图中可以清楚看出,(360-30)人与全校人数的(+)相对应,求全校人数用除法计算。列式为: (360-30)÷(+)=330÷=900(人)。 再如,甲乙两人同时从相距88千米的两地相向而行,8小时后在距中点4千米处相遇。甲比乙速度快,甲、乙每小时各行多少千米? 按照题意画线段图: 从图中可以清楚看出,甲、乙8小时各行的距离,甲行全程的一半又多出 4千米,乙行全程的一半少 4千米,这样就可以求出甲、乙的速度了。 甲速:(88÷2+4)÷8=6(千米) 乙速:(88÷2-4)÷8=5(千米) 5、表格图 有些问题,通过列表不仅能分清题目的条件和问题,而且便于区分比较,起到良好的审题作用。 如,小明3次搬运15块砖,照这样计算,小明又搬了4次,共搬多少块砖? 根据条件、问题,列出易懂的表格,能清楚看出已知条件和所求问题。 3次 15块 又搬4次 共搬?块 从表中不难看出,又搬4次和共搬多少块,这两个数量不相对应,要先求一共搬多少次,才能求出共搬多少块,列式为: 15÷3×(3+4)=35(块) 另一种思路为,先求又搬4次搬的块数,再加上原有的块数,就是共搬的块数。列式为: 15÷3×4+15=35(块) 6、思路图 有些问题因为分析的角度不同,因此解题的思路也不同。通过画图能清楚看出解题思路,便于分析比较。 如,有一个伍分币、4个贰分币、8个壹分币,要拿出8分钱,一共有多少种拿法? 这道题从表面港一点也不难,但是要不重复。不遗漏地把全部拿法一一说出来也不容易,可以用枚举法把各种情况一一列举出来,把思路写出来。 从图表中可以清楚着出不同的拿法。此题一共有不重复的7种拿法。 从以上各例题中可看出:解题时通过画图来帮助理解题意,起到了化繁为简、化难为易的作用。我们不妨在解题中广泛使用。





相关文章
- 小学数学11个计算技巧:提升孩子的计算能力!
- 小学数学概念+知识点顺口溜,考试不用愁!
- 小学数学做题宝典,加减法、乘法快速口诀表
- 小学数学一年级下册人民币单位换算100题(有答案)
- 小学数学 | 人民币换算计算方法,你家孩子掌握了吗?
- 小学数学不好?学习方法很重要!一定要告诉孩子
- 掌握这8类简算方法,小学数学简便计算再也不出错!
- 小学数学最强计算技巧总结!错过了太可惜~
- 小学数学考试中错误率较高的几种典型题
- 小学数学6类“画图”解题,快教给孩子
- 小学数学要想拿高分,必须攻克这13种典型题!赶紧为孩子收藏
- 小学数学一年级下册读数、写数练习题+应用题练习集锦,给孩子放
- 小学数学14个计算技巧:让孩子的计算能力爆表!
- 小学数学最容易出错的16个“小细节”,千万别在这上面丢分!
- 小学丨数学借用思维导图,学习简单的行程问题
- 小学数学所有公式和顺口溜都在这里了,拿走不谢!
- 这些小学数学基础知识顺口溜,让学生越读越爱学!
- 9大图形解法搞定小学数学几何易错题
- 小学数学单位换算公式大全及专项训练
- 小学数学12个估算方法详解,省去验算时间!
推荐内容
教育新鲜事
 小学语文“选词填空”汇
小学语文“选词填空”汇 小学数学11个计算技巧:
小学数学11个计算技巧: 小学数学做题宝典,加减
小学数学做题宝典,加减 小学英语自然拼读法基本
小学英语自然拼读法基本