两道数学竞赛题
(1)证明四个连续的整数的积加上1,是一个奇数的平方。
(2)把两个连续整数代入x5-x+1中,其差必是10的倍数。试证明之。
答案:(1)设四个连续的整数是n,n+1,n+2,n+3.∵n(n+1)(n+2)(n+3)+1=(n2+3n)(n2+3n+2)+1=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2其中,n2+3n+1=n(n+1)+(2n+1)因n(n+1)是连续二整数的积,一定是偶数,而2n+1是奇数,所以n2+3n+1是奇数。故连续四个整数的乘积加1是一个奇数的平方。
(2)设二连续整数是n,n+1.[(n+1)5-(n+1)+1]-(n5-n+1)=(n+1)5-n5-1=5n4+10n3+10n2+5n=5n(n3+1)+10n2(n+1)=5n(n+1)(n2-n+1)+10n2(n+1)因n(n+1)为连续二整数的积,必为偶数,所以5n(n+1)(n2-n+1)是10的倍数。
(2)把两个连续整数代入x5-x+1中,其差必是10的倍数。试证明之。
答案:(1)设四个连续的整数是n,n+1,n+2,n+3.∵n(n+1)(n+2)(n+3)+1=(n2+3n)(n2+3n+2)+1=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2其中,n2+3n+1=n(n+1)+(2n+1)因n(n+1)是连续二整数的积,一定是偶数,而2n+1是奇数,所以n2+3n+1是奇数。故连续四个整数的乘积加1是一个奇数的平方。
(2)设二连续整数是n,n+1.[(n+1)5-(n+1)+1]-(n5-n+1)=(n+1)5-n5-1=5n4+10n3+10n2+5n=5n(n3+1)+10n2(n+1)=5n(n+1)(n2-n+1)+10n2(n+1)因n(n+1)为连续二整数的积,必为偶数,所以5n(n+1)(n2-n+1)是10的倍数。
教育新鲜事
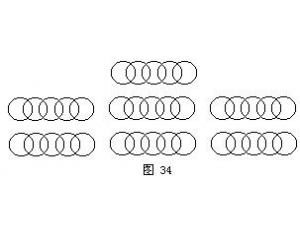 七根铁链
七根铁链 14÷2≠7吗?
14÷2≠7吗?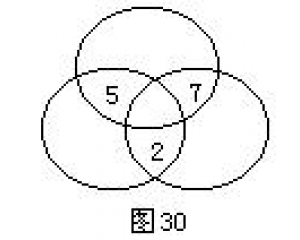 空白处填几?
空白处填几?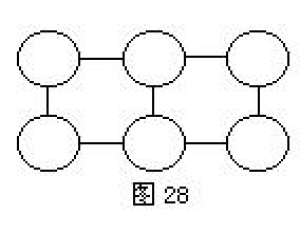 中间的两个圆圈里该填几
中间的两个圆圈里该填几