几何最值问题，应该如何解决

解决几何问题中的最值问题常用的方法有：

1、应用两点间线段最短的公理（含应用三角形的三边关系）求最值；

2、应用垂线段最短的性质求最值；

3、应用轴对称的性质求最值；

4、应用二次函数求最值；

5、应用其它知识求最值。

下面我们一起来看一些典型例题，来探讨几何问题中最值问题：

典型例题1：

解题反思：

本题主要考查了垂线段最短，以及三角形相似的性质与判定等知识点，是综合性比较强的题目，注意认真总结．

典型例题2：

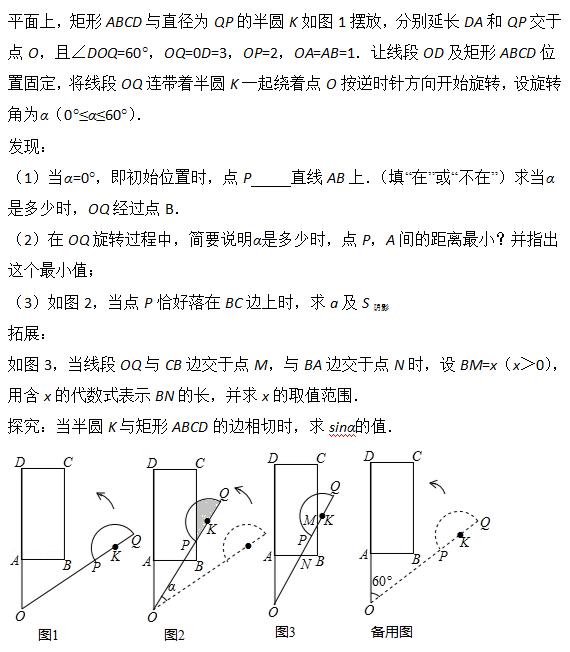
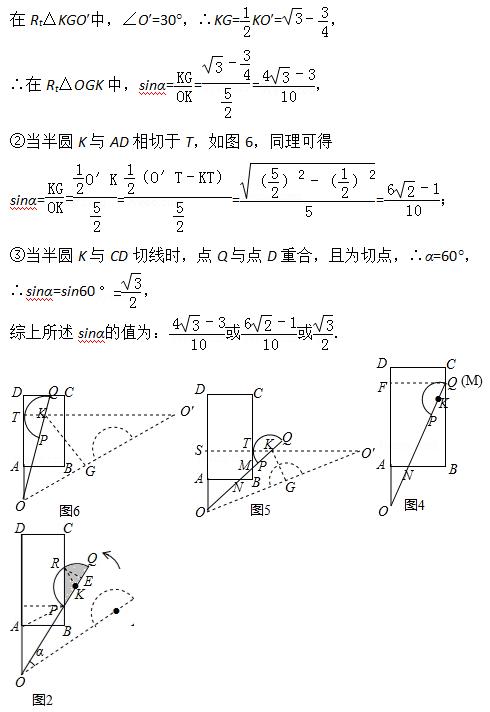
解题反思：

本题考查了矩形的性质，直线与圆的位置关系，勾股定理，锐角三角函数，根据题意正确的画出图形是解题的关键．

典型例题3：

解题反思：

本题考查了轴对称，利用轴对称确定A′、E′，连接A′E′得出P、Q的位置是解题关键，又利用了相似三角形的判定与性质，图形分割法是求面积的重要方法．

典型例题4：

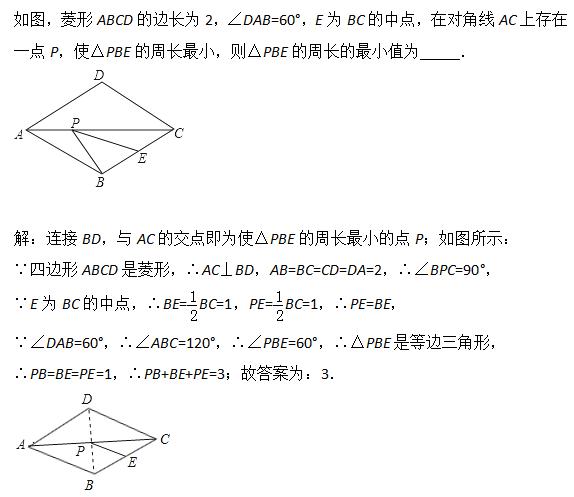
解题反思：

本题考查了菱形的性质、轴对称以及最短路线问题、直角三角形斜边上的中线性质；熟练掌握菱形的性质，并能进行推理计算是解决问题的关键．