经典几何题，一题多解

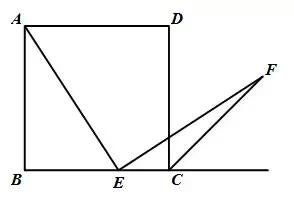
题目：如图，四边形ABCD是正方形，点E是边BC上一点，∠AEF＝90°，EF交正方形外角的平分线CF于F．求证：AE＝EF．

【方法一】

在AB上取一点G使得AG＝CE，易得△BGE为等腰直角三角形，再证明△AGE≌△ECF（ASA）即可．

【方法二】

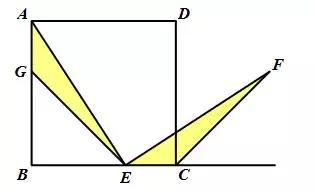
过点E作EG⊥BC交FC的延长线于点G，证明△AEC≌△FEG（ASA）即可．

【方法三】

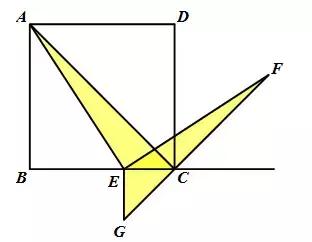
延长AC至点G使得CG＝CF并连接EG，证明△ECF≌△ECG（SAS），再得∠ECA＝∠G（提示：外角的性质）即可．

【方法四】

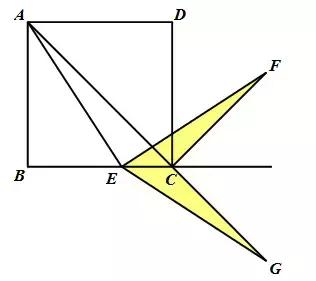
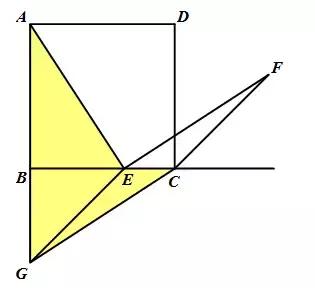
分别延长AB，FC交于点G，并连接EG，证明△ABE≌△GBE（SAS），再证∠EGC＝∠F（提示：外角的性质）即可．

【方法五】

延长AB至点G，使得BG＝BE，并连接EG，CG，证明△ABE≌△CBG（SAS），再证明四边形EGCF为平行四边形即可（两组对边分别平行）．

【方法六】

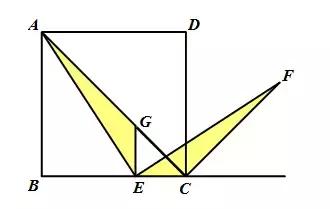
连接AC，过点E作EG⊥BC，交AC于点G，证明△AEG≌△FEC（ASA）即可．

【方法七】

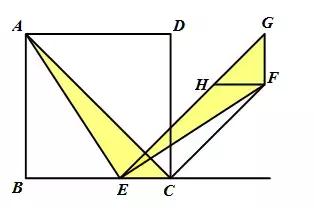
如图，分别过点E，F作EG∥CF，FG∥CD和FH∥BC，EG分别与FG，FH交于点G，H，易得四边形ECFH为平行四边形，再证明△ACE≌△EGF（ASA）即可．

【方法八】

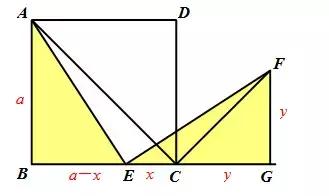
过点F作FG⊥BC于点G，分别设AB＝a，EC＝x，FG＝CG＝y，则BE＝a－x，根据△ABE∽△EGF得AB：BE＝EG：GF，即a：（a－x）＝（x＋y）：y，得ay＝ax＋ay－x2－xy，得x（a－x－y）＝0，即a＝x＋y，所以AB＝EG，BE＝FG所以AE＝EF．

【总结】本题还有许多其他构造辅助线的方法来证明，有的是同种类型的不同构法，异曲同工。欢迎大家讨论！

当然，除了一题多解之外，大家也可以考虑把条件和结论对调进行证明，要不试试看？

题目：如图，四边形ABCD是正方形，点E是边BC上一点，在正方形外角的平分线CF上取一点F使得AE＝EF．

求证：∠AEF＝90°．