数学破题36计第29计 向量开门 数形与共
第29计 向量开门 数形与共?
●计名释义?
非数学问题数学化,说的是数学建模,非运算问题运算化,向量是典型的代表.?
向量是近代数学的最重要和最基本的概念之一,有深刻的几何背景,是解决几何问题的有力工具.同时,它又具有代数运算的功能.因此,它像一个媒婆,牵起了一根线,一头连着代数,另一头连着图形,只要经它轻轻一拉,数形便能结合成一家人.??
●典例示范?)
【例1】
α,β为锐角,且sinα-sinβ=![]() ,?cosα-cosβ=
,?cosα-cosβ=![]() ,求tan(α-β)之值.?
,求tan(α-β)之值.?
【解答】 如图,设A(cosα,?sinα),
B(cosβ,?sinβ)为单位圆上两点,
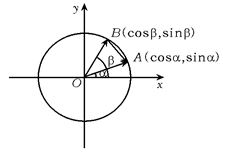 由条件知:0<α<β<
由条件知:0<α<β<![]() .?
.?
那么:![]()
=(cosα- cosβ,?sinα- sinβ)
=![]() .?
.?
∴|![]() |=
|=![]() ,|
,|![]() |=|
|=|![]() |=1.?
例1题解图
|=1.?
例1题解图
△OAB中,由余弦定理:cos(α-β)= cos
(β-α) =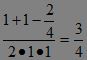 .?
.?
∴?sin(α-β)=![]() ,??tan(α-β)=
,??tan(α-β)=![]() .?
.?
【点评】 如果说本例用向量求三角函数值中没有太大的优越性,那么利用向量
模型证明不等式则有其独到的简便之处,再看下例.??
【例2】
设a,b,c,d∈R,证明:ac+bd≤![]() ?
?
【解答】 设m=(a,b),n=(c,d),则mn=ac+bd,|m|·|n|=![]()
?∵m·n=|m|·ncos(m,n)≤|m|·|n|.? ∴ac+bd≤![]() .?
.?
【点评】 难以置信的简明,这正是向量的半功伟绩之一,那么,向量在解析几
何中又能起作用吗???
【例3】 在平行六面体ABCD—A1B1C1D1中,以顶点A为端点的三条棱长都是1,且两两夹角均为60°,则对角线AC1?之长为 .?
【思考】 求线段的长度常用的手段是归结为解三角形.利用勾股定理或余弦定理,显然,这种方法需要较大的计算量,例如,确定AC1与平面ABCD所成角的大小就不是省油的灯.有无更好的方法呢?这个平行六面体的各个表面不都是边长相等且夹锐角为60°的菱形吗?利用向量岂不更为省事??
向量的数量积公式可以保驾护航.?
对!走向量法解题的道路.?
【解答】 如图所示,![]()
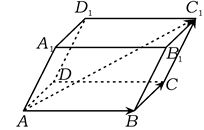 ∴
∴![]() ?
?
=![]()
![]()
=1+1+1+2(cos60°+ cos60°+ cos60°)=6?
∴|![]() |=
|=![]() .?
例2题解图
.?
例2题解图
【点评】 向量运算的优越性,由本例已可一览无遗,特别是|![]() |2=
|2=![]() 的运用奇妙.?注意:
的运用奇妙.?注意:![]() 与
与![]() 所成角等于
所成角等于![]() 与
与![]() 所成角,是60°而不是120°.
所成角,是60°而不是120°.
 ●对应训练?
●对应训练?
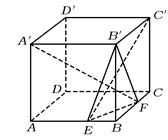
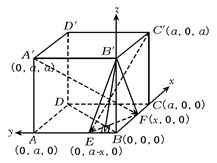
1?如图,在棱长为a的正方体
ABCD—A′B′C′D′中,E、F
分别是AB、AC上的动点,满足AE=BF.?
(Ⅰ)求证:![]() ;?
;?
(Ⅱ)当三棱锥B′—BEF的体积取得最大值时,
求二面角B′—EF—B的大小(结果用反三角函数表示).? 第1题图
2?已知a,b∈R+,且a≠b,求证:(a3+b3)2<(a2+b2)(a4+b4).?
3?在双曲线xy=1上任取不同三点A,B,C,证明△ABC的垂心也在该双曲线上.??
●参考答案?
1.(1)如图,以B为原点,直线BC,BA,BB′分别为x,y,z轴建立空间直角坐标系,并设![]() =x,则有:A′(0,a,a),C′(a,0,a). E(0,a-x,0),F(x,0,0),∴
=x,则有:A′(0,a,a),C′(a,0,a). E(0,a-x,0),F(x,0,0),∴![]() =(x,-a,-a),
=(x,-a,-a),![]() =(-a,a-x,-a).?
=(-a,a-x,-a).?
∵![]() ·
·![]() =(x,-a,-a)(-a,a-x,-a)=-ax-a2+ax+a2=0,
=(x,-a,-a)(-a,a-x,-a)=-ax-a2+ax+a2=0,
∴?![]() ⊥
⊥![]() .?
.?
 (2)VB′—BEF?=
(2)VB′—BEF?=![]() S△EEF·|
S△EEF·|![]() |=
|=![]() ·
·![]() (a-x)·x·a
(a-x)·x·a
=![]() a(a-x)·x≤
a(a-x)·x≤![]() a·
a·![]() ,
,
当且仅当a-x=a,即x=![]() 时,?
时,?
(VB′—BEF)max =![]() ,
,
此时E、F分别为AB,BC的中点,必EF⊥BD.?
设垂足为M,连B′M,∵BB′⊥平面ABCD, 第1题图
由三垂线定理知B′M⊥EF,∠BMB′是二面角B′—EF—B的平面角,?
设为θ,∵|![]() |=
|=![]() ∴?tanθ=
∴?tanθ=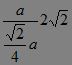 .?
.?
即θ=arctan2![]() ,则二面角B′—EF—B的大小为arctan2
,则二面角B′—EF—B的大小为arctan2![]() .?
.?
2?设m=(a,b),n=(a2,b2), ∵m·n≤|m|·|n|.?
∴a3+b3≤![]() ,即是(a3+b3)2≤(a2+b2)(a4+b4).?
,即是(a3+b3)2≤(a2+b2)(a4+b4).?
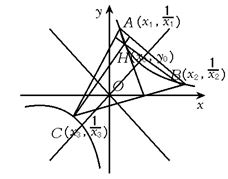 3?如图,设A(x1,
3?如图,设A(x1,![]() ),B(x2,
),B(x2,![]() ),
),
C(x3,![]() ),△ABC的垂心为H(x0,y0),
),△ABC的垂心为H(x0,y0),
则![]() ,?
,?
![]() ,?
第3题解图
,?
第3题解图
∵![]() ,?∴(x0-x3)(x2-x1)+(y0-
,?∴(x0-x3)(x2-x1)+(y0-![]() ·
·![]() .?
.?
∵x1≠x2,∴x0-x3![]() .?
.?
∴x0+![]() (1)?
(1)?
同理:x0+![]() .?
.?
∴x2-x1=y0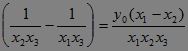 .
.
∵x1≠x2,∴y0=-x1x2x3,代入 (1):x0-![]() =x3
=x3![]() =0,?
=0,?
∴x0y0=1,即H(x0,y0)在双曲线xy=1上.??
相关文章
- 高中数学空间向量解立体几何,如此简单! ?
- 高中数学空间向量解立体几何汇总,如此简单!速来看!!
- 高中数学多样解题,一题突破平面向量所有难点!
- 高考数学难点34导数的运算法则及基本公式应用
- 高考金钥匙数学解题技巧大揭秘专题七 三角恒等变换与解三角形
- 高考金钥匙数学解题技巧大揭秘专题十三 空间线面位置关系的推理
- 2017高考数学 平面向量四心向量表示大突破
- 高中数学平面向量知识点总结
- 高考数学难点突破15三角函数的图象和性质
- 高考金钥匙数学解题技巧大揭秘专题十四 用空间向量法解决立体几
- 高考金钥匙数学解题技巧大揭秘专题六 三角函数的图象和性质
- 数学破题36计第11计 耗子开门 就地打洞
- 数学破题36计第34计 参数开门 宾主谦恭
- 数学破题36计第27计 方程开门 欲擒故纵
- 数学破题36计第3计 诸葛开门 扇到成功
- 数学破题36计第14计 鲜花开门 情有独钟
- 2017高考数学平面向量的应用
- 2017高考数学平面向量的数量积
推荐内容
教育新鲜事
 高中数学“函数”必考知
高中数学“函数”必考知 高考数学答题方法的19条
高考数学答题方法的19条 高考数学干货丨最容易出
高考数学干货丨最容易出 【高中数学】《三角函数
【高中数学】《三角函数