数学破题36计第27计 方程开门 欲擒故纵

第27计 方程开门 欲擒故纵?

●计名释义?

数学，顾名思义，是关于数的科学.于是，数的运算和求值就成了数学的首要内容.数学的主干内容——函数、方程和不等式都是关于数的内容.

?方程和函数是从两个不同的方向研究数的关系.从映射的角度看问题，函数研究的是“从数到象”，而方程相反，研究的是“从象到数（原象）”.?

方程解题步骤：（1）设x. 对数（原象x）先作假设；（2）放x. 把这个“假”x放到函数（笼子）中去.(3)关x. 按函数解析式的运算，列出一个等式——方程（笼子关闭）.(4)擒x，解这个方程，把x抓出来.??

●典例示范?

【例1】     求二项式展开式中的常数项.?

【分析】     这是数学运算中的“求值”问题，解决问题的工具是函数和方程式，为了设方程，先得找函数.?

【解答】     由二项展开式的通项公式T_r+1=C

【插语】     在n为常数的条件下，这是一个关于r的函数式T（r)=f(r)?

【续解】     由此得T_r+1=C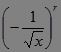r=…=（-1）^rCx?

欲T_r+1为常数，只须=0.?

【插语】     按“函数值”满足的条件，转入方程.?

【续解】     解方程，得r=4.故所求的常数项为T₅=(-1)⁴C=210.?

【点评】     欲擒故纵是方程解题的基本策略.“欲擒”体现了列方程；“故纵”体现于将对象“放到”函数中去“入套”.??

【例2】     求?sin20°cos70°+sin10°sin50°?的值.?

【解答】     令x=sin20°cos70°+sin10°sin50°?，构造与之对应的对偶式y=cos20°sin70°+cos10°cos50°?,?

则x+y=（sin20°cos70°+cos20°sin70°)+(sin10°sin50°+cos10°cos50°)?

=sin90°+cos40°=1+cos40°?                                   ①?

x-y=（sin20°cos70°-cos20°sin70°）+(sin10°sin50°-cos10°cos50°)?

=sin(20°-70°)+cos(10°+50°)=-cos40°-]?                       ②?

①+②得x=，故sin20°cos70°+sin10°sin50°=.?

【点评】     构造方程组，利用对偶方程组解决问题，是充分借助方程思想解题的方法之一.??

【例3】     已知双曲线C：（1-a²)x²+a²y²=a²(a>1)，设该双曲线上支的顶点为A，且上支与直线y=-x相交于P点，一条以A为焦点，M(0,m)为顶点,开口向下的抛物线通过点P. 设PM的斜率为k，且≤k≤，求实数a的取值范围.?

【解答】     由双曲线方程知A(0,1),则抛物线方程为?         x²=-4(m-1)(y-m),?

由双曲线与直线相交解得点P的坐标为(-a,a)，又因为点P在抛物线上,?

∴a²=-4(m-1)(a-m)                                   ①?

而MP的斜率为k=，故m=ak+a.?

将m=ak+a代入①得a²=-4(ak+a-1) (-ak),?

即4ak²+4(a-1)k-a=0                                  ②?

根据题意,方程②在区间[，]上有实根.?

令f (k)=4ak²+4(a-1)k-a，则其对称轴方程为                 k=<0?

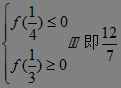∴≤a≤4.?         ∴实数a的取值范围为［,4］.?

【点评】     根据直线与圆锥曲线的位置关系,构造含参数的方程,转化为根的分布问题求解.??

【例4】     （Ⅰ）已知数列{c_n}，其中c_n=2ⁿ+3ⁿ，且数列{c_n+1-pc_n}为等比数列，求常数p的值；（Ⅱ）设{a_n}，{b_n}是公比不相等的两个等比数列，c_n=a_n+b_n，求证：数列{c_n}不是等比数列.?

【解答】     （Ⅰ）由题意知c₂-pc₁，c₃-pc₂，c₄-pc₃成等比数列，?

∴(c₃-pc₂)²=(c₂-pc₁)(c₄-pc₃)，展开整理得?         (c²₂-c₁c₃)p²+(c₁c₄-c₂c₃)p+c²₃-c₂c₄=0.?

将c₁=5，c₂=13，c₃=35，c₄=97代入上式得p²=-5p+6=0，解得p=2或p=3.?

而当p=2时,=3;?            当p=3时，=2.均适合.?

故满足条件的p的值为2或3.?

（Ⅱ）假设数列{c_n}是等比数列，则c²₂=c₁c₃，即(a₂+b₂)²=(a₁+b₁)(a₃+b₃)，?

故(a₁q+b₁r)²=(a₁+b₁)(a₁q²+b₁r²)，其中q，r分别是{a_n}，{b_n}的公比.?

化简整理，得a₁b₁r²+a₁b₁q²-2a₁b₁qr=0，即(q-r)²=0，解得q=r.?

这与题设中两数列公比不相等矛盾，因此数列{c?n}不是等比数列.?

【点评】     这里选取等比数列的前三项，根据等比中项的意义列方程求出p的值，再验证一般情况.第(Ⅱ)问的反证法中，也是通过构建方程获证.??

●对应训练?

1.设(2-x)⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵，则a₁+a₃+a₅=                      .?

2.已知椭圆=1(a>b>0)，A,B的椭圆上两点，线段AB的垂直平分线与x轴交于点P(x₀,0)，求证：?.?

3.设{a_n}为等差数列，S_n为数列{a_n}的前n项和，已知S₇=7，S₁₅=75，T_n为数列的前n项和，求T_n.??

●参考答案?

1.分析     本式为二项式展开式中的偶数项系数和，而不是偶数项二项式系数和，不能直接用二项式系数性质求解，但可用赋值法构造方程求解.?

解：由于f (x)=(2-x)⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵?

令x=1得：f (1)=(2-1)⁵=a₀+a₁+a₂+a₃+a₄+a₅=1                         ①?

令x=-1得f (-1)=［2-(-1)］⁵=a₀-a₁+a₂-a₃+a₄-a₅=3⁵                     ②?

两式相加再除以2得：a₁+a₃+a₅=-121.?

2.证明     若AB的中点为M,?

AB的垂直平分线为l：y=k(x-x₀)              ①?

由于l与x轴相交,因此k≠0，故k_AB=.?

又k_OM·（）=，故k_OM =,?

∴OM所在直线方程为y=x,代入①得x=k(x-x₀).?

因此所证的结论变为方程的解在椭圆内的取值范围问题.?

故由上述方程解得x=x₀.  (x为点M的横坐标)?

但点M在椭圆=1内部，即-a<x₀<a,?

解得-<x₀<.?

点评     用方程思想解决某些范围问题特别简单,容易找出问题的突破口.?

3.设等差数列{a_n}的前n项和S_n=an²+bn.?

由S₇=7，S₁₅=75，得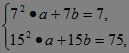即解得a=，b=?

∴S_n=n²n.  ∴.?

∴数列是首项为-2，公差为的等差数列.?

故T_n=n² n.?

点评     因为等差数列（公差不为0）的前n项和公式是关于n的二次函数，因此可将等差数列的前n项和直接设为S_n=an²+bn的形式，往往能达到化繁为简的目的。

简的目的