高考专题:数列求和方法归析

方法一:分组转化
把数列分为特殊数列即等差(比)数列,然后利用公式求解,要分清楚哪些项构成等差数列,哪些项构成等比数列;等比数列中注意对公比q是否为1的讨论.

方法二:错位相减法
这种方法是在推导等比数列的前n项和公式时所用的方法,这种方法主要用于求数列{an·bn}的前n项和,其中{ an }、{ bn }分别是等差数列和等比数列,为了更好的进行相减,在第一个式子中最好把倒数第2项也写出来,减后一定要搞清楚哪些消去了,还剩哪些,等比数列中注意对公比q是否为1的讨论.




方法三:裂项相消
这是分解与组合思想在数列求和中的具体应用. 裂项相消法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 在正负项抵消后,要注意看是否只剩了第一项和最后一项,有的前面剩两项,后面也剩两项或更多项,主要取决于两个分母相差多少。常见的通项分解(裂项)如:



 方法四:倒序相加
方法四:倒序相加
如果一个数列{an},与首末项等距的两项之和等于首末两项之和或等于同一个常数,可采用把正着写与倒着写的两个和式相加,就得到一个常数列的和,这一求和方法称为倒序相加法.例如:等差数列前n项和公式的推导,用的就是“倒序相加法”.
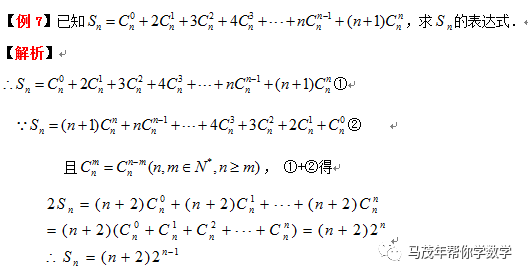
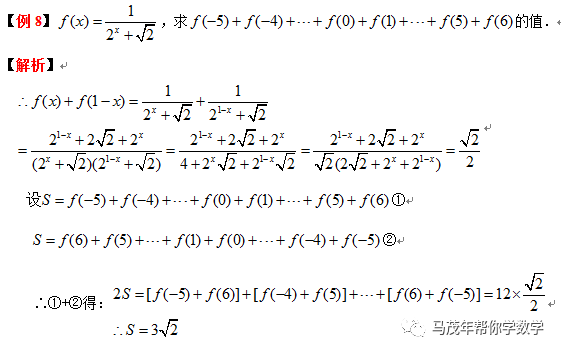
推荐内容
教育新鲜事
 高中丨(高频考点)物理
高中丨(高频考点)物理 期末考试时间定了!收官
期末考试时间定了!收官 高中生逆袭物语:这几步
高中生逆袭物语:这几步 必须收藏!省略句考点全
必须收藏!省略句考点全