菲涅耳提出部分曳引假说
对于阿拉果的人眼选择光速的假设,菲涅耳认为很难令人信服。他在1918年给阿拉果写信,指出这种解释不可取。为了使两个实验的结果能够协调,他提出了部分曳引假说,即在透明物体中,以太可以部分地被这一物体拖曳。他再假设透明物体的折射率决定以太的密度,令ρ与ρ1分别表示真空中和透明物体中以太的密度,假设这些密度与折射率的平方成正比,则:
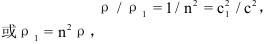




教育新鲜事
 “超声“和“超音”
“超声“和“超音” 集市一瞥
集市一瞥 昆明湖上
昆明湖上 背道而驰
背道而驰