克劳修斯提出熵的概念
一般认为,克劳修斯在1865年提出了熵的概念,其实,早在1854年,即最初形成热力学第二定律之后不到四年,他在《热的机械论中第二个基本理论的另一形式》一文中提出了“变换的等价性”,用一个符号N表示变换,这个符号N就是熵S的前身。克劳修斯特别注意到了不可逆性,这是热力学概念发展中的又一台阶。他将可逆循环和不可逆循环作了区别。
然后又定义“温度t时功转变为热量Q的变换等价值”为Q·f(t),其中f(t)为温度t的一个函数,他还规定功转变为热和热从高温转移到低温为正的变换。他又定义f(t)=1/T,T为“温度的未知函数”。这样,变换的等价值为Q/T。克劳修斯用符号N代表一个循环中变换的总值,得:
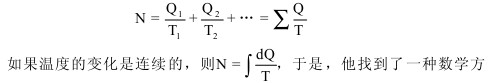
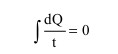
到了1865年,克劳修斯发表《热的动力理论的基本方程的几种方便形式》,文中他明确用T表示绝对温标。关于热力学第二定律,他写道:

然后又定义“温度t时功转变为热量Q的变换等价值”为Q·f(t),其中f(t)为温度t的一个函数,他还规定功转变为热和热从高温转移到低温为正的变换。他又定义f(t)=1/T,T为“温度的未知函数”。这样,变换的等价值为Q/T。克劳修斯用符号N代表一个循环中变换的总值,得:
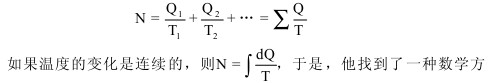
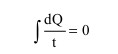
到了1865年,克劳修斯发表《热的动力理论的基本方程的几种方便形式》,文中他明确用T表示绝对温标。关于热力学第二定律,他写道:

教育新鲜事
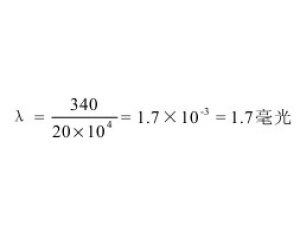 “超声“和“超音”
“超声“和“超音” 集市一瞥
集市一瞥 昆明湖上
昆明湖上 背道而驰
背道而驰