有趣的“魔术数”
你知道“魔术数”吗?将自然数N接写在另一个自然数的右边(例如,将 2接着写在34的右边就是342),如果得到的新数都能被N整除,那么自然数N就叫做魔术数。小朋友,在小于100的自然数中,你能找到多少个这样的魔术数,它们各是几?分析与解 我们首先发现1就是一个魔术数。因为不管把1写在哪一个自然数右边,所得的新数都能被1整除。在剩下的八个自然数中,可以断定3、4、6、7、8、9这六个自然数不是魔术数。这只要把这六个数分别接着写在1后面就可以明白了。那么剩下的2和5是不是魔术数呢?回答是肯定的。因为把2接写在任何一个自然数的右边,所得的新数的个位上的数字总是2,这些新数一定能被2整除,所以2是魔术数。
同样道理,5也是魔术数,这样我们就找到了三个一位魔术数:1、2、5。我们再寻找两位魔术数。两位数从10到99为止,一共是90个。我们先把每一个两位数接写在1后面,很快就能发现,除了10、20、25、50以外,其余的两位数都不能整除被接在1后面所得的新数,当然就肯定不是魔术数了。那么10、20、25、50这四个数是不是魔术数呢? 10是魔术数很容易确定。20也是魔术数,因为把20接写在自然数a后面,新数就是(100a+20),而100a+20=20×(5a+1),显然能被20整除。用上述办法同样可以证明:25、50也是魔术数。
这样,我们就找到了四个二位魔术数10、20、25、50。细心的小朋友从上面找魔术数的过程中一定会发现,一位魔术数 1、2、5恰好是10的约数中所有的一位数;二位魔术数10、20、25、50恰好是100(102)的约数中的所有的二位数。那么,三位魔术数是不是1000(103)的约数中的所有的三位数?四位魔术数是不是 104的约数中的所有四位数?进而n位魔术数是不是10n的约数中的所有n位数?是的。不信你试试看。顺便告诉你,三位魔术数和三位以上的魔术数都是五个。这又是为什么?请你想想看。
同样道理,5也是魔术数,这样我们就找到了三个一位魔术数:1、2、5。我们再寻找两位魔术数。两位数从10到99为止,一共是90个。我们先把每一个两位数接写在1后面,很快就能发现,除了10、20、25、50以外,其余的两位数都不能整除被接在1后面所得的新数,当然就肯定不是魔术数了。那么10、20、25、50这四个数是不是魔术数呢? 10是魔术数很容易确定。20也是魔术数,因为把20接写在自然数a后面,新数就是(100a+20),而100a+20=20×(5a+1),显然能被20整除。用上述办法同样可以证明:25、50也是魔术数。
这样,我们就找到了四个二位魔术数10、20、25、50。细心的小朋友从上面找魔术数的过程中一定会发现,一位魔术数 1、2、5恰好是10的约数中所有的一位数;二位魔术数10、20、25、50恰好是100(102)的约数中的所有的二位数。那么,三位魔术数是不是1000(103)的约数中的所有的三位数?四位魔术数是不是 104的约数中的所有四位数?进而n位魔术数是不是10n的约数中的所有n位数?是的。不信你试试看。顺便告诉你,三位魔术数和三位以上的魔术数都是五个。这又是为什么?请你想想看。
教育新鲜事
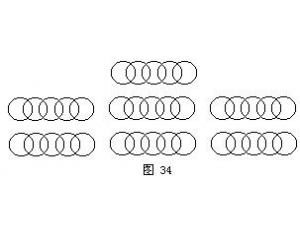 七根铁链
七根铁链 14÷2≠7吗?
14÷2≠7吗?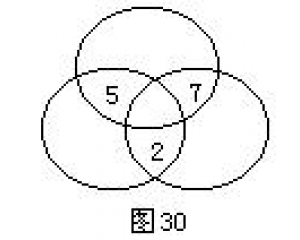 空白处填几?
空白处填几?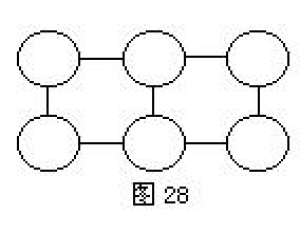 中间的两个圆圈里该填几
中间的两个圆圈里该填几