不等式的基本性质知识点
目标:不等式的基本性质及其应用
实数及其大小的比较
1.实数的两大特征
实数的两大特征,一是任意一个实数的平方都大于等于0;二是任意两个实数都可以比较大小,反之,可以比较大小的两个数也一定是实数。
2.比较两个实数大小的依据。
实数和数轴上的点是一一对应的,一个数在数轴上就是一个点,数轴上的一个点,就是一个数;所以,在不至引起混淆的情况下,我们认为“数a”和“点a”有着相同的内涵;两个不同的实数a、b,与数轴上两个不同的点A、B相对应,规定右边的点所表示的数比左边的点所表示的数要大,因此正数都大于0,负数都小于0。
结合数轴以及实数减法的意义,我们可以看到:如果A在B的右边,a > b,这时a-b > 0;如果A在B的左边,a < b ,这时a-b < 0;如果A、B重合,a = b,这时a-b = 0,反之也成立。 因此我们有如下公理:
公理(实数大小的比较原则):
如果a-b是正数,则a>b;a-b > 0 Û a > b
如果a-b是负数,则a<b;a-b = 0 Û a = b
如果a-b等于零,则a=b;反之也成立。 即: a-b < 0 Û a < b
根据这一公理,要比较两数的大小,只要将这两数作差,由差与0的大小关系,就可以推得这两数的大小。

推荐内容
教育新鲜事
 四种命题的形式及等价关
四种命题的形式及等价关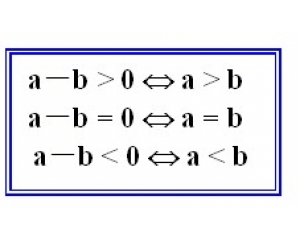 不等式的基本性质知识点
不等式的基本性质知识点 《一元二次不等式的解法
《一元二次不等式的解法 历年含函数知识点的高考
历年含函数知识点的高考