药真的有效吗—假设检验
在生活中充满大最虚假广告,有的宣传药多么多么有效,治愈了多少多少人,有效率达90%甚至更高;有的宣传产品精良,次品率很小很小;但是,这种宣传并不可靠,可是一般人也没有办法澄清事实。然而,统计学却有一套检验方法来判断假设是否真的成立。如果一种新药有疗效的话,什么叫疗效显著。费希尔的显著性检验的步骤如下:(1)假设的概率分布中参数的假设值;(2)如假设值是真的参数值,有一个检验统计量,而且分布完全知道;(3)来自总体的一个随机样本;(4)由样本计算出统计量;(5)当假设为真时,计算检验统计量取像实际观察到的那么大极端值的概率。这个概率称为是显著水平,根据它我们可以进行判断:如果这个概率很小,或者假设不真,或者假设是真的。但是却发生一件小概率事件。1933年,小皮尔逊和波兰统计学家耐曼发展了统计假设检验理论,他们的理论更为严谨,而且对统计的哲学思想有所突破。他们实质上把假设检验当作一个决策过程,要对于两个可能的假设做出接受其中一个的决策。一个假设称为原假设,另一个假设称为备样假设,如果经过一定的程序接受或拒绝原假设,我们有四种情况可能发生: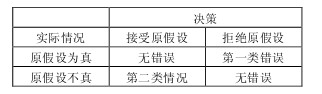

教育新鲜事
 分马
分马 龟鹤算
龟鹤算 藏盗法
藏盗法 草纸算术趣题
草纸算术趣题