中考数学选择题精选及答案
中考数学选择题精选及答案
1.在平面直角坐标系中,抛物线y=a(x-1)2+k与x轴交于A、B两点,顶点为C,点D在抛物线的对称轴上,若四边形ACBD是一个边长为2且有一个内角为60°的菱形,则该抛物线的解析式有( )
 A.2个
B.3个
C.4个
D.5个
A.2个
B.3个
C.4个
D.5个
2.已知,如图,过正方形ABCD的顶点A作对角线BD的平行线,在这条线上取一点E,使BE=BD,连结DE,则∠AED等于( ).
A.100° B.105° C.110° D.115°
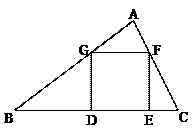 3.如图,在△ABC中,D、E在边BC上,F、G分别在边AC、AB上,且四边形DEFG为正方形。如果S△CFE =S△AGF =1,S△BDG =3,那么S△ABC等于(
).
3.如图,在△ABC中,D、E在边BC上,F、G分别在边AC、AB上,且四边形DEFG为正方形。如果S△CFE =S△AGF =1,S△BDG =3,那么S△ABC等于(
).
A.6 B.7 C.8 D.9
4.如图,已知AD是△ABC的中线,BC=6,且∠ADB=45°,∠C=30°,则AB=( ).
 A.
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
5.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A、B、C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( ).
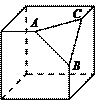

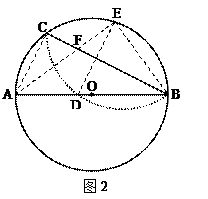
6.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( )个.
A.2个 B.3个 C.4个 D.5

7.如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为( ).
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
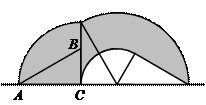
 8.如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2=
8.如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2=![]() ,则BC=( ).
,则BC=( ).
A.![]() B.π C.
B.π C.![]() D.
D.![]()
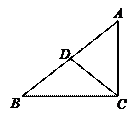 9.如图,已知直角三角形ABC的周长为
9.如图,已知直角三角形ABC的周长为![]() ,斜边上的中线CD=1,则△ABC的面积为( ).
,斜边上的中线CD=1,则△ABC的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
10.如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则BC等于( ).
 A.14
B.13 C.
A.14
B.13 C.![]() D.
D.![]()
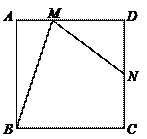 11.如图,在正方形ABCD中,M是AD上异于D的点,N是CD的中点,且∠AMB=∠NMB,则AM : AB=( ).
11.如图,在正方形ABCD中,M是AD上异于D的点,N是CD的中点,且∠AMB=∠NMB,则AM : AB=( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.如图,△ABC是锐角三角形,正方形DEFG一边在BC上,其余两个顶点分别在AB、AC上,记△ABC的面积为S1,正方形的面积为S2,则( ).
A.S1≥2S2 B.S1≤2S2 C.S1>2S2 D.S1<2S2

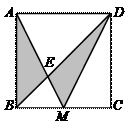
13.如图,已知正方形ABCD的面积为1,M是BC的中点,则图中阴影部分的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.如图,AB是定长线段,圆心O是AB的中点,AE、BF为半圆的切线,E、F为切点,且AE=BF,G是弧EF上的动点,过G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( ).
A.正比例函数y=kx B.一次函数y=kx-b(b≠0)
 C.反比例函数y=
C.反比例函数y=![]() D.二次函数y=ax 2+bx+c
D.二次函数y=ax 2+bx+c
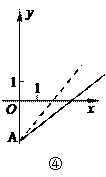
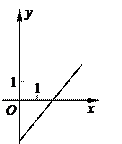 15.右图是某条公共汽车线路收支差额y与乘客量x的图像(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出两条建议:建议(1)是不改变
15.右图是某条公共汽车线路收支差额y与乘客量x的图像(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出两条建议:建议(1)是不改变![]() 车票价格,减少支出费用;建议(2)是不改变支出费用,提高车票价格。下面给出四个图像(如图所示)则(
)
车票价格,减少支出费用;建议(2)是不改变支出费用,提高车票价格。下面给出四个图像(如图所示)则(
)
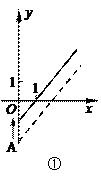
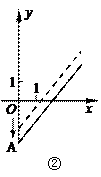
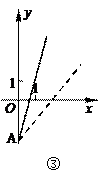
![]()
A.①反映了建议(2),③反映了建议(1) B.①反映了建议(1),③反映了建议(2)
C.②反映了建议(1),④反映了建议(2) D.④反映了建议(1),②反映了建议(2)
16.已知函数y=3-(x-m)(x-n),并且a,b是方程3-(x-m)(x-n)=0的两个根,则实数m,n,a,b的大小关系可能是( ).
A.m<a<b<n B.m<a<n<b C.a<m<b<n D.a<m<n<b
17.已知f(x)=1-(x-a)(x-b),并且m,n是方程f(x)=0的两根,则实数a,b,m,n的大小关系可能是( ).
A.m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
 18.如图,将一圆形纸片沿着弦BC折叠后,圆弧恰好经过直径AB上一点D,使得AD=5,BD=7,则折痕BC的长为( ).
18.如图,将一圆形纸片沿着弦BC折叠后,圆弧恰好经过直径AB上一点D,使得AD=5,BD=7,则折痕BC的长为( ).
A.10 B.![]() C.
C.![]() D.11
D.11
19.如图,以半圆的一条弦BC为对称轴将弧BC折叠后与直径AB交于点D,若![]() =
=![]() ,且AB=10,则CB的长为( ).
,且AB=10,则CB的长为( ).
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
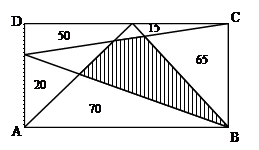
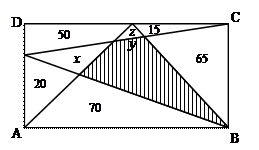
 20.如图,矩形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为( ).
20.如图,矩形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为( ).
A.80 B.85 C.90 D.95
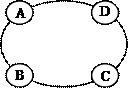
21.如下图是某汽车维修公司的维修点环形分布如图。公司在年初分配给A、B、C、D四个维修点某种配件各50件。在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行。那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为( ).
 A.15 B.16 C.17 D.18
A.15 B.16 C.17 D.18
22.如图,把Rt△ABC依次绕顶点C沿水平线翻转两次,若∠C=90°,AC=![]() ,
,
BC=1,那么AC边从开始到结束所扫过的图形的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
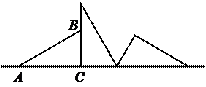
23.如图,在Rt△ABC中,∠BAC=90°,AB=3,M为边BC上的点,连结AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是( ).
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
24.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数为x、y、z,则![]() 的值为( ).
的值为( ).
A.1 B.![]() C.
C.![]() D.
D.![]()
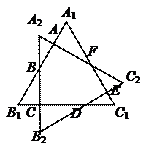 25.如图,两个全等的边长为正整数的正△A1B1C1和正△A2B2C2的中心重合,且满足A1B1⊥A2C2,若六边形ABCDEF的面积为S=
25.如图,两个全等的边长为正整数的正△A1B1C1和正△A2B2C2的中心重合,且满足A1B1⊥A2C2,若六边形ABCDEF的面积为S=![]() -
-![]() ,其中,m、n为有理数,则
,其中,m、n为有理数,则![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
26.如图,在菱形ABCD中,∠DAB=120°,点E平分DC,点P在BD上,
且PE+PC=1,那么,边AB长的最大值是( ).
 A.1
B.
A.1
B.![]() C.
C.![]() D.
D.![]()
27.如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且四边形PQOB的面积是![]() ,AB=2,则点P的坐标为( ).
,AB=2,则点P的坐标为( ).
 A.(
A.(![]() ,
,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
28.铁链是由铁环相扣组成的,某铁链的铁环尺寸如图所示,那么,一段由这种相同的铁环环环相扣组成的长14.5米的铁链,共有( )个铁环.
A.224 B.225 C.226 D.227
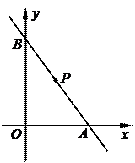 29.如图,一次函数的图象经过点P(2,3),交x轴的正半轴于点A,交y轴的正半轴于点B,则△AOB面积的最小值为(
).
29.如图,一次函数的图象经过点P(2,3),交x轴的正半轴于点A,交y轴的正半轴于点B,则△AOB面积的最小值为(
).
A.9 B.10 C.11 D.12
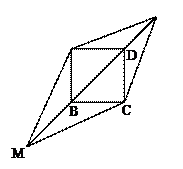
30.如图,正方形ABCD的边长为1,M,N为BD所在直线上的两点,且AM=![]() ,∠MAN=135°,则四边形AMCN的面积为( ).
,∠MAN=135°,则四边形AMCN的面积为( ).
A.![]() B.2 C.
B.2 C.![]() D.
D.![]()
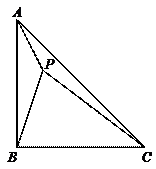 31.如图,在△ABC中,∠ABC=90°,AB=BC=5,P是△ABC内一点,且PA=
31.如图,在△ABC中,∠ABC=90°,AB=BC=5,P是△ABC内一点,且PA=![]() ,PC=5,则PB=( ).
,PC=5,则PB=( ).
A.![]() B.3 C.
B.3 C.![]() D.4
D.4
32.如图,△ABC被DE、FG分成面积相等的三部分(即S1=S2=S3),且DE∥FG∥BC,BC=![]() ,则FG -DE=( ).
,则FG -DE=( ).
 A.
A.![]() -1
B.
-1
B.![]() -
-![]() C.
C.![]() -
-![]() D.2-
D.2-![]()
33.如图,在△ABC中,AB=AC,∠BAC=80°,P在△ABC中,∠PBC=10°,∠PCB=30°,则∠PAB的度数为( ).
A.50° B.60° C.65° D.70°
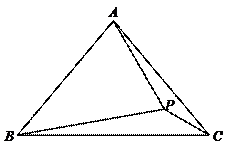
34.如图,在△ABC中,AB=AC,∠BAC=80°,P在△ABC中,∠PBC=10°,∠PCB=20°,则∠PAB的度数为( ).
A.50° B.60° C.65° D.70°
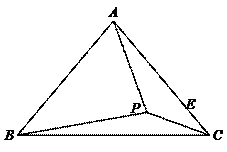

35.如图,“L”形纸片由五个边长为1的小正方形组成,过A点剪一刀,刀痕是线段BC,若阴影部分面积是纸片面积的一半,则BC的长为( ).
A.
B.4 C.
D.
36.如图,O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为( ).
A.2 B.C.
D.3
37.已知二次函数y=ax 2+bx+c,且a<0,a+b+c>0,则一定有( ).
A.b 2-4ac>0 B.b 2-4ac=0 C.b 2-4ac≥0 D.b 2-4ac≤0
38.如果圆内接四边形的边长依次是25,39,52,60,则这个圆的直径是( ).
A.62 B.63 C.65 D.69
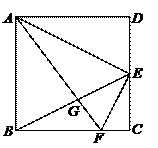 39.如图,设ABCD是正方形,E是CD边的中点,点F在BC边上,且DAEF=90°,AF与BE相交于点G,则BG : GE=( ).
39.如图,设ABCD是正方形,E是CD边的中点,点F在BC边上,且DAEF=90°,AF与BE相交于点G,则BG : GE=( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
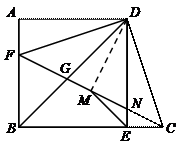
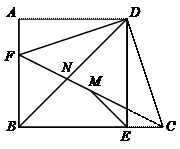 40.如图,直角梯形ABCD中,∠A=90°,AD∥BC,AB=AD,DE⊥BC于E,点F为AB上一点,且AF=EC,点M为FC的中点,连结FD、DC、ME,设FC与DE相交于点N,下列结论:①∠FDB=∠FCB;②△DFN∽△DBC;③FB=
40.如图,直角梯形ABCD中,∠A=90°,AD∥BC,AB=AD,DE⊥BC于E,点F为AB上一点,且AF=EC,点M为FC的中点,连结FD、DC、ME,设FC与DE相交于点N,下列结论:①∠FDB=∠FCB;②△DFN∽△DBC;③FB=![]() ME;④ME垂直平分BD,其中正确结论的个数是( ).
ME;④ME垂直平分BD,其中正确结论的个数是( ).
A.1个 B.2个 C.3个 D.4个
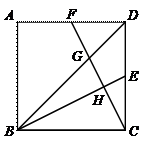
41.如图,点E、F分别是正方形ABCD的边CD、AD的中点,BD、BE分别交CF于点G、H,若正方形ABCD的面积是240,则四边形DGHE的面积等于( ).
A.26 B.28 C.24 D.30
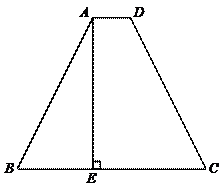 42.如图,等腰梯形ABCD中,AD∥BC,AB=CD,AC=BC,AE⊥BC于E,AD : AE=1
: 4,若AB=
42.如图,等腰梯形ABCD中,AD∥BC,AB=CD,AC=BC,AE⊥BC于E,AD : AE=1
: 4,若AB=![]() ,则梯形ABCD的面积等于( ).
,则梯形ABCD的面积等于( ).
A.44 B.46 C.48 D.50
43.如图,AD、BE、CF是△ABC的三条高,若AB=6,BC=5,EF=3,则线段BE的长为( ).
A.![]() B.4
C.
B.4
C.![]() D.
D.![]()
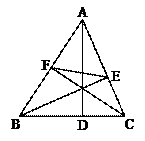
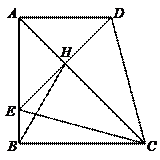
44.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.若沿对角线AC折叠梯形ABCD,点D恰与AB边上的点E重合,且∠BCE=15°,连结DE,交AC于H,连接BH.下列结论:①△CDE为等边三角形;②△BHE∽△ADC;③∠BHC=∠BCD;④EH=2BE;⑤四边形BCHE的面积=△ADC的面积,其中正确结论的个数是( ).
A、①③④ B、②③⑤ C、①③⑤ D、①④⑤
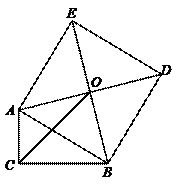 45.如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABDE,正方形的中心为O,且OC=
45.如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABDE,正方形的中心为O,且OC=![]() ,那么,则BC的长等于(
).
,那么,则BC的长等于(
).
A.![]() B.5 C.
B.5 C.![]() D.
D.![]()
46.已知函数y=k|x|与y=x+k的图象恰有两个公共点,则实数k的取值范围是( ).
A.k >1 B.-1<k<1
C.k ≤-1和k ≥1 D.k <-1和k >1
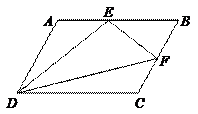 47.已知:如图,平行四边形ABCD中,点E、F分别在边AB、BC上,且△ADE、△BEF、△CDF的面积分别为5、3、4,则△DEF的面积为( ).
47.已知:如图,平行四边形ABCD中,点E、F分别在边AB、BC上,且△ADE、△BEF、△CDF的面积分别为5、3、4,则△DEF的面积为( ).
A.5 B.6 C.7 D.8
48.二次函数y=-x 2+2x+8的图像与x轴交于B,C两点,点D平分BC,若在x轴上方的A点为抛物线上的动点,且∠BAC为锐角,则AD的取值范围是( ).
A.3< AD ≤9 B.3≤ AD ≤9 C.4< AD ≤10 D.3≤ AD ≤8
49.如图,正方形ABCD和CEFG的边长分别为a、b(b>2a),把正方形ABCD绕点C旋转一周,在旋转的过程中,△AEG 的面积S的取值范围是( ).
A.a 2≤ S ≤b 2 B.![]() a 2≤ S ≤
a 2≤ S ≤![]() b 2
b 2
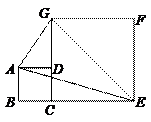 C.
C.![]() b 2-ab≤ S ≤
b 2-ab≤ S ≤![]() b 2+ab D.b 2-ab≤ S ≤b 2+ab
b 2+ab D.b 2-ab≤ S ≤b 2+ab
50.如图,在矩形内画了一些直线,已知边上有三块面积分别是13,35,49,那么图中阴影部分的面积是( ).
A.97 B.98 C.99 D.100

51.如图,已知AD、BE分别是△ABC的BC、AC边上的中线,交点为O.且AD⊥BE,若BC=![]() ,AC=
,AC=![]() ,则AB的长为(
).
,则AB的长为(
).
A.4 B.5 C.6 D.7
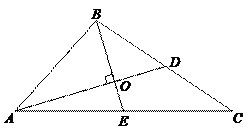
52.在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为A(6,6),B(-4,3),C(-1,-7),则该正方形在第一象限的面积是( ).
A.25 B.36 C.49 D.30
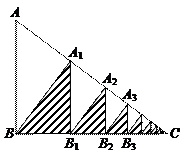 53.如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作BA1⊥AC,过A1作A1B1⊥BC,得阴影Rt△A1BB1;再过B1作B1A2⊥AC,过A2作A2B2⊥BC,得阴影Rt△A2B1B2;……如此下去,则得到的所有阴影三角形的面积之和为( ).
53.如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作BA1⊥AC,过A1作A1B1⊥BC,得阴影Rt△A1BB1;再过B1作B1A2⊥AC,过A2作A2B2⊥BC,得阴影Rt△A2B1B2;……如此下去,则得到的所有阴影三角形的面积之和为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 54.如图,△ABC的面积为24,AD是BC边上的中线,E在AD上,且AE : ED=1 : 2,BE的延长线交AC于点F.则△AEF的面积为( ).
54.如图,△ABC的面积为24,AD是BC边上的中线,E在AD上,且AE : ED=1 : 2,BE的延长线交AC于点F.则△AEF的面积为( ).
A.![]() B.1
C.
B.1
C.![]() D.
D.![]()

55.如图,点G是△ABC的重心,GA=4,GB=5,GC=3,则△ABC的面积为( ).
A.18 B.20 C.22 D.24
56.若0< x <1,则x 2,x,![]() ,
,![]() 这四个数中( ).
这四个数中( ).
A.![]() 最大,x 2最小
B.x最大,
最大,x 2最小
B.x最大,![]() 最小
最小
B
C.x 2最大,![]() 最小
D.x最大,x 2最小
最小
D.x最大,x 2最小
 57.如图,在△ABC中,D、E分别在BC、AC上,且AE=2CE,BD=2CD,AD、BE交于点F,若S△ABC =6,则四边形DCEF的面积为( ).
57.如图,在△ABC中,D、E分别在BC、AC上,且AE=2CE,BD=2CD,AD、BE交于点F,若S△ABC =6,则四边形DCEF的面积为( ).
A.![]() B.
B.![]() C.1
D.
C.1
D.![]()
58.方程(x 2+x-1)x+3=1的所有整数解的个数是( ).
A.5 B.4 C.3 D.2
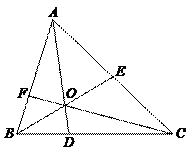 59.如图,在△ABC中,E是AC的中点,O是BE的中点,连结AO并延长交BC于D,连结CO并延长交AB于F,若△ABC的面积为1,则四边形BDOF的面积为( ).
59.如图,在△ABC中,E是AC的中点,O是BE的中点,连结AO并延长交BC于D,连结CO并延长交AB于F,若△ABC的面积为1,则四边形BDOF的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
60.使方程2x 2-5mx+2m 2=5的二根为整数的整数m的值共有( ).
A.1个 B.2个 C.3个 D.4个
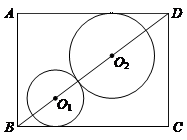
61.如图,矩形纸片ABCD中,AB=3,BC=4,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( ).
 A.
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
62.已知二次函数y=ax 2+bx+c的图象如图所示,
记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( ).
A.p>q B.p=q
C.p<q D.p、q大小关系不能确定
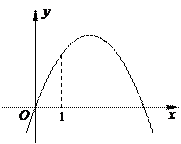
63.如图,已知正方形ABCD的面积为1,以AB为边在正方形内作等边三角形
ABE,则阴影部分的面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

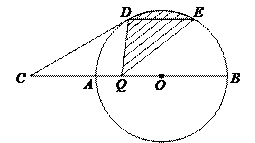
64.如图,AB是⊙O的直径,点C在BA的延长线上,且CA=1,CD切⊙O于D点,CD=![]() AB,DE∥AB交⊙O于E点,动点Q在直径AB上,则阴影部分的面积为( ).
AB,DE∥AB交⊙O于E点,动点Q在直径AB上,则阴影部分的面积为( ).
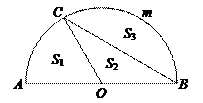 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
65.如图,AB为半圆O的直径,C为半圆上一点,且∠COA=60°.设扇形AOC、△COB、弓形BmC的面积分别为S1,S2,S3,则它们之间的大小关系是( ).
A.S1<S2<S3 B.S2<S1<S3
C.S1<S3<S2 D.S3<S2<S1
 66.如图,已知△ABC,D是AB上的一点,DE∥AC交AC于点E,DF∥AC交BC于点F,若△ADE、△DBF的面积分别为1和2,则四边形DECF的面积为( )
66.如图,已知△ABC,D是AB上的一点,DE∥AC交AC于点E,DF∥AC交BC于点F,若△ADE、△DBF的面积分别为1和2,则四边形DECF的面积为( )
A.3
B.2 C.![]() D.
D.![]()
67.如图,平行四边形ABCD中,P、Q分别是BC、CD的中点,则和△ABP面积相等的三角形有( ).
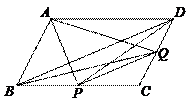 A.3个 B.4个
C.5个
D.6个
A.3个 B.4个
C.5个
D.6个
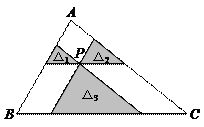 68.如图,过△ABC内一点P分别作△ABC三边的平行线,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是9,16和64,则△ABC的面积是( )
68.如图,过△ABC内一点P分别作△ABC三边的平行线,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是9,16和64,则△ABC的面积是( )
A.178 B.200 C.196 D.225
69.如图,梯形ABCD中,AD∥BC,O是对角线的交点,若△AOD、△BOC的面积分别为4和16,则梯形ABCD的面积为( ).
A.36 B.30 C.40 D.32

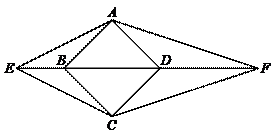
70.如图,已知正方形ABCD的边长为2,点E、F均在直线BD上,且∠EAF=135°,EB : DF=1 : 2,下列结论:①△ABE∽△FDA;②∠AEF=30°;③CF=![]() ;④四边形AECF的面积为10,其中正确结论的个数是( ).
;④四边形AECF的面积为10,其中正确结论的个数是( ).
A.1个 B.2个 C.3个 D.4个
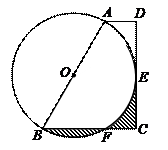 71.如图,梯形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O与CD相切于E,与BC相交于F,若AB=8,AD=2,则图中阴影部分的面积为( ).
71.如图,梯形ABCD中,AD∥BC,∠D=90°,以AB为直径的⊙O与CD相切于E,与BC相交于F,若AB=8,AD=2,则图中阴影部分的面积为( ).
A.3 B.![]() C.
C.![]() D.
D.![]()
72.如图,在四边形ABCD中,一组对边AB=CD,另一组对边AD≠BC,分别取AD、BC的中点M、N,连结MN,则AB与MN的大小关系是( ).
A.AB=MN B.AB>MN C.AB<MN D.上述三种情况均可能出现
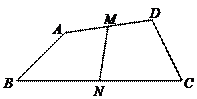
73.抛物线y=ax 2与直线x=1,x=2,y=1,y=2围成的正方形有公共点,则a的取值范围是( ).
A.![]() ≤ a ≤2
B.
≤ a ≤2
B.![]() ≤ a ≤1 C.
≤ a ≤1 C.![]() ≤ a ≤2
D.
≤ a ≤2
D.![]() ≤ a ≤1
≤ a ≤1
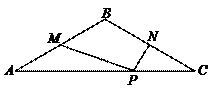 74.如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M,N分别是AB,BC的中点,若PM+PN的最小值为2,则△ABC的周长是(
).
74.如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上的一个动点,M,N分别是AB,BC的中点,若PM+PN的最小值为2,则△ABC的周长是(
).
A.12
B.2+![]() C.4
D.4+
C.4
D.4+![]()
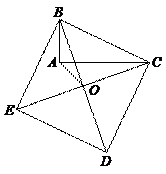 75.如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCDE,设正方形的中心为O,连结AO,如果AB=4,AO=
75.如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCDE,设正方形的中心为O,连结AO,如果AB=4,AO=![]() ,那么AC的长等于( ).
,那么AC的长等于( ).
A.12
B.8
C.![]() D.
D.![]()
76.如图,等边三角形ABC的边长和⊙O的周长相等,当⊙O按箭头方向从某一位置沿△ABC的三边做无滑动旋转,直至回到原出发位置时,则⊙O共转了( ).
A.4圈 B.3圈
C.5圈 D.3.5圈
77.已知y=x 3+ax 2+bx+c,当x=5时,y=50;当x=6时,y=60;当x=7时,y=70.则当x=4时,y=( ).
A.30 B.34 C.40 D.44
78.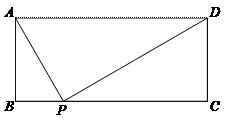 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系一定满足( ).
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系一定满足( ).
A.a ≥![]() b
B.a ≥b
C.a ≥
b
B.a ≥b
C.a ≥![]() b
D.a ≥2b
b
D.a ≥2b
 79.二次函数y=ax 2+bx+c的图象如图所示,Q(n,2)是图象上的一点,且AQ⊥BQ,则a的值为( )
79.二次函数y=ax 2+bx+c的图象如图所示,Q(n,2)是图象上的一点,且AQ⊥BQ,则a的值为( )
A.-![]() B.-
B.-![]() C.-1
D.-2
C.-1
D.-2
80.若![]() =
=![]() =
=![]() =t,则一次函数y=tx+t 2的图象必定经过的象限是(
)
=t,则一次函数y=tx+t 2的图象必定经过的象限是(
)
A.第一、二象限 B.第一、二、三象限 C.第二、三、四象限 D.第三、四象限
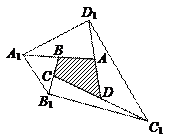
81.如图,任意四边形ABCD的面积为S,作点A关于B点的对称点A1,点B关于点C的对称点B1,点C关于点D的对称点C1,点D关于点A的对称点D1,连结A1B1C1D1,则四边形A1B1C1D1的面积为( )
 A.2S
B.3S
C.4S
D.5S
A.2S
B.3S
C.4S
D.5S
82.将一张边长分别为a,b(a>b)的矩形纸片ABCD折叠,使点C与点A重合,则折痕的长为( )
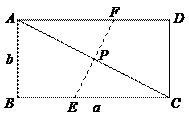 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
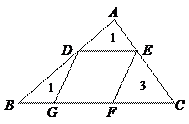 83.如图,平行四边形DEFG内接于△ABC,已知△ADE、△DBG、△EFC的面积为1、3、1,那么平行四边形DEFG的面积为( )
83.如图,平行四边形DEFG内接于△ABC,已知△ADE、△DBG、△EFC的面积为1、3、1,那么平行四边形DEFG的面积为( )
A.![]() B.2
C.3
D.4
B.2
C.3
D.4
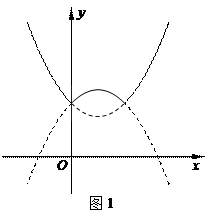
84.函数y=1-|x-x 2|的图象大致形状是( )
A.图1中的实线部分 B.图2中的实线部分
C.图3中的实线部分 D.图4种的实线部分
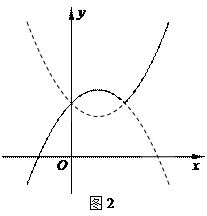
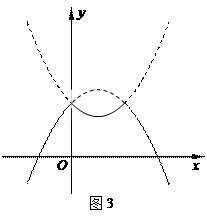
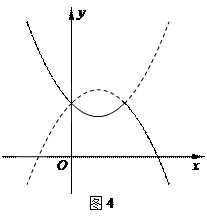
85.函数y=1-|x-x 2|的图象是( )


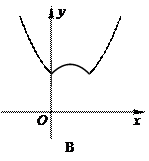

86.对于每个x,函数y是y1=2x,y2=x+2,y3=-![]() x+12这三个函数中的最小值,则函数y的最大值是( )
x+12这三个函数中的最小值,则函数y的最大值是( )
A.4
B.6
C.8
D.![]()
 87.如图,边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在抛物线y=ax 2(a <0)的图像上,则该抛物线的解析式为( )
87.如图,边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在抛物线y=ax 2(a <0)的图像上,则该抛物线的解析式为( )
A.y=-![]() x 2 B.y=-
x 2 B.y=-![]() x 2
x 2
C.y=-2x 2 D.y=-![]() x 2
x 2
88.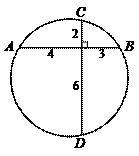 如图,圆内两条弦互相垂直,其中一条被分成长为4和3两段,另一条被分成长为2和6两段,则此圆的直径为( )
如图,圆内两条弦互相垂直,其中一条被分成长为4和3两段,另一条被分成长为2和6两段,则此圆的直径为( )
A.![]() B.8 C.
B.8 C.![]() D.9
D.9

89.如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW.若OA+OB+OC=1,则OC=( )
A.2-![]() B.
B.![]() -1
C.6-
-1
C.6-![]() D.
D.![]() -3
-3
 90.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB
90.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB
A.1 B.2 C.3 D.4
91.如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE的长为( ).
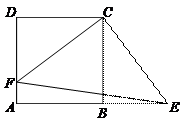 A.10
B.11
C.12 D.15
A.10
B.11
C.12 D.15
92.图1~图4是四个全等的等腰直角三角形,图1和图2中的阴影都是正方形,其面积分别为S1和S2;图3中的阴影是一个半圆,其直径在等腰直角三角形的直角边上,面积为S3;图4中的阴影是一个内切圆,其面积为S4。则下列判断正确的是( )
①S1=S2;②S3=S4;③在S1,S2,S3,S4中,S2最小.
A.①② B.②③ C.①③ D.①②③
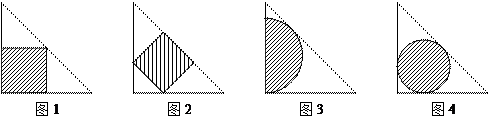
93.如图,△ABC三边的长分别是a,b,c,且![]() =
=![]() ,BD=c,则∠CAB与∠CBA的关系是( )
,BD=c,则∠CAB与∠CBA的关系是( )
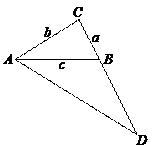 A.∠CBA>2∠CAB
B.∠CBA≥2∠CAB
A.∠CBA>2∠CAB
B.∠CBA≥2∠CAB
C.∠CBA=2∠CAB D.不确定
94.已知函数f(x)=x 2+λx,p、q、r为△ABC的三边,且p < q <r,若对所有的正整数p、q、r都满足f(p)<f(q)<f(r),则λ的取值范围是( ).
A.λ >-2 B.λ >-3 C.λ >-4 D.λ >-5
 95.如图,直线l交y轴于点C,与双曲线y=
95.如图,直线l交y轴于点C,与双曲线y=![]() (k<0)交于A、B两点,P是线段AB上的点(不与A、B重合),Q为线段BC上的点(不与B、C重合),过点A、P、Q分别向x轴作垂线,垂足分别为D、E、F,连结OA、OP、OQ,设△AOD的面积为S1、△POE的面积为S2、△QOF的面积为S3,则有( )
(k<0)交于A、B两点,P是线段AB上的点(不与A、B重合),Q为线段BC上的点(不与B、C重合),过点A、P、Q分别向x轴作垂线,垂足分别为D、E、F,连结OA、OP、OQ,设△AOD的面积为S1、△POE的面积为S2、△QOF的面积为S3,则有( )
A.S1<S2<S3 B.S3<S1<S2
C.S3<S2<S1
D.S1、S2、S3的大小关系无法确定![]()
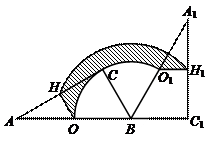 96.如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O,H分别为边AB,AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为( )
96.如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O,H分别为边AB,AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为( )
A.![]() B.
B.![]()
C.![]() D.π
D.π
97.已知抛物线y=ax 2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,且抛物线的顶点在直线y=-1,若△ABC为直角三角形,则△ABC面积的最大值为( )
A.1 B.![]() C.2 D.3
C.2 D.3
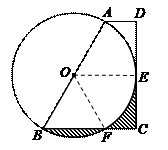
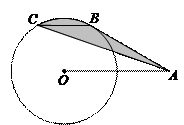 98.如图,A是半径为1的⊙O外一点,OA=2,AB切⊙O于点B,弦BC∥OA,连结AC,则图中阴影部分的面积为( )
98.如图,A是半径为1的⊙O外一点,OA=2,AB切⊙O于点B,弦BC∥OA,连结AC,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
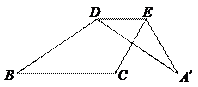
99.如图,将△ABC沿着它的中位线DE折叠后,点A落在点A′处,若∠C=120°,∠A=26°,则∠A′DB的度数是( )
A.112° B.100° C.120° D.110°
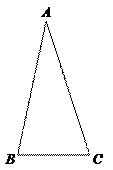
100.如图,△ABC中,∠A=30°,E是AC边上的点,先将△ABE沿BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿BD翻折,C点恰好落在BE上,此时∠CDB=82°,则原三角形∠B的度数是( )
A.72° B.74° C.76° D.78°
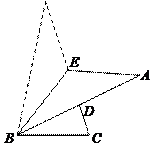

 101.如图,在△ABC中,∠CAB=60°,D,E分别是边AB,AC上的点,且∠AED=60°,EC=DB+DE,∠CDB=2∠CDE,则∠DCB的度数是( )
101.如图,在△ABC中,∠CAB=60°,D,E分别是边AB,AC上的点,且∠AED=60°,EC=DB+DE,∠CDB=2∠CDE,则∠DCB的度数是( )
A.15° B.20° C.25° D.30°
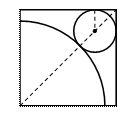
102.如图,在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型,该圆的半径为r,扇形的半径为R,则圆的半径r与扇形的半径R之间的关系为( )
A.R=3r B.R=![]() r
C.R=
r
C.R=![]() r
D.R=4r
r
D.R=4r
103.已知:△ABC中,∠A :∠B :∠C=1 : 2 : 4,设BC=a,AC=b,AB=c,则下列结论正确的是( )
A.![]() +
+![]() =
=![]() B.a 2=bc
C.b 2=c(a+c) D.a+c=2b
B.a 2=bc
C.b 2=c(a+c) D.a+c=2b
104.如图,在半径为1的⊙O中,直径AB把⊙O分成上、下两个半圆,点C是上半圆上一个动点(C与点A、B不重合),过点C作弦CD⊥AB,垂足为E,∠OCD的平分线交⊙O于点P,设CE=x,AP=y,下列图象中,能反映y与x之间函数关系的是( )

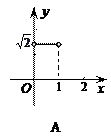

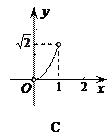
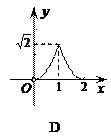
105.已知函数y=ax 2+bx+c,当y>0时,-![]() <x<
<x<![]() ,则函数y=cx 2-bx+a的图象可能是下图中的( )
,则函数y=cx 2-bx+a的图象可能是下图中的( )
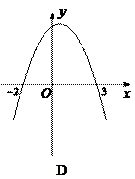
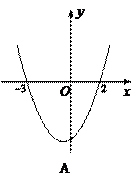
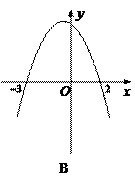
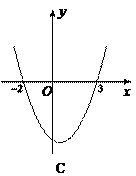
106.如图,四边形ABCD的两组对边AD、BC与AB、DC的延长线分别交于点E、F,∠AEB、∠AFD的平分线交于点P,若∠A=60°,∠BCD=136°则下列结论正确的是:①∠EPF=100°②∠ADC+∠ABC=60°③∠PEB+∠PFC+∠EPF=136°④∠PEB+∠PEC=36°正确的是( )
A.①②③ B.②③④ C.①③④ D.①②③④
107.在△ABC中,最大角∠A是最小角∠C的两倍,且AB=7,AC=8,
则BC=( )
A.![]() B.10 C.
B.10 C.![]() D.
D.![]()
108.已知△ABC的三条边长是三个连续的自然数,且最大角是最小角的
两倍,则△ABC的最小边长等于( )
A.3 B.4 C.5 D.6
109.已知二次函数y=ax 2+bx+c的图象与x轴交于点(-2,0),(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的下方.下列结论:
①4a-2b+c=0;②a <b<0;③2a+c>0;④2a-b+1>0.其中正确结论的个数是( )
 A.4个 B.3个
C.2个 D.1个
A.4个 B.3个
C.2个 D.1个
110.已知二次函数y=ax 2+bx+c的图象如图所示,
设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|,则( )
A.M>0 B.M=0
C.M<0 D.不能确定M为正、为负或为0
111.如图,Rt△ABC的面积为60,∠BAC=90o,D是BC中点,DE⊥AB于点E,AD、CE交于点F,则△AEF的面积为( )
 A.9
B.10
C.11 D.12
A.9
B.10
C.11 D.12
112.设x1,x2是一元二次方程x 2+x-3=0的两根,则x13-4x22+19
等于( )
A.-4 B.8 C.6 D.0
113.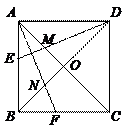 如图,正方形ABCD中,E、F分别在AB、BC上,AF平分∠BAC,DE⊥AF,DE交AC于M,AF交BD于N,记x=
如图,正方形ABCD中,E、F分别在AB、BC上,AF平分∠BAC,DE⊥AF,DE交AC于M,AF交BD于N,记x=![]() ,y=
,y=![]() ,z=
,z=![]() ,则(
)
,则(
)
A.x>y>z B.x=y=z C.x=y>z D.x>y=z
114.若直角三角形的两条直角边长为a、b,斜边长为c,斜边上的高为h,则
下列关系正确的是( ).
A.ab=h 2 B.![]() =
=![]()
C.![]() =
=![]() D.a 2+b 2=2h 2
D.a 2+b 2=2h 2
115.如图,矩形纸片ABCD中,M、N分别为AB、CD的中点,将纸片折叠,使A点落在MN上,得到△ABE,再过A点折叠纸片,使C点落在直线BC上,折痕为PQ.下列结论:①△PAE∽△ABE;②∠ABE=30°;③S△PAE : S△QBA : S△ABE =1 : 3 : 4;④若沿直线EA折叠纸片,则点B一定与点D重合,其中正确结论的个数是( )
 A.1个 B.2个
C.3个 D.4个
A.1个 B.2个
C.3个 D.4个

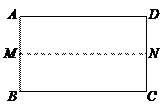
116.如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
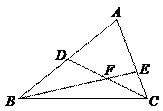 117.如图,在△ABC中,D是AB的中点,点E在AC上,
117.如图,在△ABC中,D是AB的中点,点E在AC上,![]() =2,BE与CD相交于点F.若△BCF的面积为1,则△ABC的面积为(
)
=2,BE与CD相交于点F.若△BCF的面积为1,则△ABC的面积为(
)
A.3
B.![]() C.4 D.
C.4 D.![]()
118.已知△ABC为锐角三角形,⊙O经过点B、C,且与边AB、AC分别相交于点D、E.若⊙O的半径与△ADE的外接圆的半径相等,则⊙O一定经过△ABC的( ).
A.内心 B.外心 C.重心 D.垂心
119.如图,△ABC中,AD、BE相交于点O,BD : CD=3 : 2,AE : CE=2 : 1,那么S△BOC : S△AOC : S△AOB为( )
 A.2 : 3 : 4 B.2 : 3 : 5 C.3 : 4 : 5 D.3 : 4 : 6
A.2 : 3 : 4 B.2 : 3 : 5 C.3 : 4 : 5 D.3 : 4 : 6
120.用[x]表示不大于x的最大整数,则方程x 2-2[x]-3=0的解的个数为( )
A.1个 B.2个 C.3个 D.4个
121.如图,大圆恰好盖住了小圆一半的面积,设小圆的直径为d,则大圆在小圆内的弧长与d相比,正确的是( )
A. >d B. <d C. =d D. ≥d
122.如图是反比例函数y=![]() ,x ≤-2和x ≥1时的部分图象,且其图象过点(2,1),若二次函数y=ax 2
,x ≤-2和x ≥1时的部分图象,且其图象过点(2,1),若二次函数y=ax 2
的图象与上述图象有公共点,则a的取值范围是( )
A.-2≤ a ≤1且a≠0 B.a ≤-2或a ≥1
C.-![]() ≤ a ≤2且a≠0 D.a ≤-
≤ a ≤2且a≠0 D.a ≤-![]() 或a ≥2
或a ≥2
选择题答案
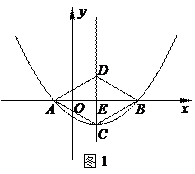
1.C
解:设抛物线的对称轴与x轴交于点E
如图1,当∠CAD=60°时,则DE=1,BE=![]()
∴B(1+![]() ,0),C(1,-1)
,0),C(1,-1)
将B(1+![]() ,0),C(1,-1)代入y=a(x-1)2+k,解得k=-1,a=
,0),C(1,-1)代入y=a(x-1)2+k,解得k=-1,a=![]()
∴y=![]() (x-1)2-1
(x-1)2-1
 如图2,当∠ACB=60°时,由菱形性质知A(0,0),C(1,
如图2,当∠ACB=60°时,由菱形性质知A(0,0),C(1,![]() )
)
将A(0,0),C(1,![]() )代入y=a(x-1)2+k,解得k=-
)代入y=a(x-1)2+k,解得k=-![]() ,a=
,a=![]()
∴y=![]() (x-1)2-
(x-1)2-![]()
同理可得:y=-![]() (x-1)2+1,y=-
(x-1)2+1,y=-![]() (x-1)2+
(x-1)2+![]()
所以符合条件的抛物线的解析式共4个
2.B
 解:如图,过A作AG⊥BD于G,过E作EH⊥BD于H,则AG=BG=
解:如图,过A作AG⊥BD于G,过E作EH⊥BD于H,则AG=BG=![]() BD
BD
∵AE∥DB,∴四边形AEHG为矩形,∴EH=AG=![]() BD
BD
又BE=BD,∴EH=![]() BE,∴∠EBH=30°
BE,∴∠EBH=30°
∵BE=BD,∴∠BDE=∠BED=![]() (180°-30°)=75°
(180°-30°)=75°
∴∠AED=105°
3.D
解:设DE=x,则EC=![]() ,BD=
,BD=![]() ,BC=x+
,BC=x+![]()
由△AGF∽△ABC得:![]() =
=![]() ,∴x 4=16,x=2,∴正方形DEFG的面积为4
,∴x 4=16,x=2,∴正方形DEFG的面积为4
∴S△ABC=1+1+3+4=9
4.C
解:如图,过A作BC的垂线交CB的延长线于H,则HD=AH,HC=![]() AH
AH
∴HC-HD=(![]() -1)AH=3,∴AH=
-1)AH=3,∴AH=![]() (
(![]() +1),HB=
+1),HB=![]() (
(![]() +1)-3=
+1)-3=![]() (
(![]() -1)
-1)
 ∴AB=
∴AB=![]() =
=![]()
5.B
6.D
∠ACD、∠BAD、∠ODA、∠ODE、∠OED
 7.D
7.D
解:如图,则有
 解得:a=
解得:a=![]() ,r=
,r=![]()
8.A
解:如图,连结BD
S1=![]() π×32-S△ABD-S弓形=
π×32-S△ABD-S弓形=![]() ,S2=
,S2=![]() AB·BC-S△ABD-S弓形
AB·BC-S△ABD-S弓形
S1-S2=![]() π×32-
π×32-![]() AB·BC=
AB·BC=![]() ,AB·BC=8π,BC=
,AB·BC=8π,BC=![]()
9.B
解:由已知得:AB+AC+BC=2CD+AC+BC=2+AC+BC=![]() ,∴AC+BC=
,∴AC+BC=![]()
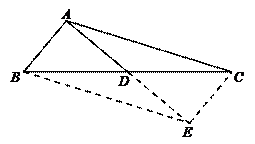 ∴(AC+BC)2=AC 2+BC 2+2AC·BC=5
∴(AC+BC)2=AC 2+BC 2+2AC·BC=5
又AC 2+BC 2=AB2=(2CD)2=4,∴2AC·BC=1
∴S△ABC=![]() AC·BC=
AC·BC=![]()
10.C
解:如图,延长AD至E,使DE=AD,连结BE、CE,则四边形ABEC是平行四边形
∴BE=AC=13,∴AB 2+AE 2=52+122=169=132=BE 2
∴△ABD是直角三角形
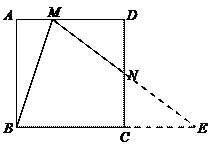 ∴BD=
∴BD=![]() =
=![]() =
=![]() ,∴BC=
,∴BC=![]()
11.A
解:如图,延长MN交BC的延长线于点E
∵∠AMB=∠NMB,∠AMB=∠MBC,∠NMB=∠MBC,∴BE=ME
易知△NDM≌△NCE,∴CE=MD,MN=NE,∴ME=2MN
设正方形边长为2,MD=x,则AM=2- x,DN=1,BE=x+2
在直角三角形DMN中,由勾股定理得:MN=![]() ,∴ME=
,∴ME=![]()
∴x+2=![]() ,解得:x=0(不合题意,舍去),或x=
,解得:x=0(不合题意,舍去),或x=![]()
∴AM=2-![]() =
=![]() ,AM : AB=
,AM : AB=![]()
12.A
解:设正方形DEFG的边长为x,△ABC的BC边上的高为h
由△AGF∽△ABC得:![]() =
=![]() ,∴x=
,∴x=![]() ,∴S2=
,∴S2=![]()
又S1=![]() ,∴
,∴![]() =
=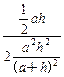 =
=![]() ·
·![]() ≥
≥![]() ·
·![]() =1
=1
∴S1≥2S2
13.B
 解:由△BEM∽△AED得:
解:由△BEM∽△AED得:![]() =
=![]() =
=![]() ,∴BM边上的高=
,∴BM边上的高=![]() AB=
AB=![]()
∴S阴影=2(![]() -
-![]() )=
)=![]()
14.C
解:如图,连结OE、OF、OC、OD、OG
∵AE、BF为半圆的切线,∴OE⊥AE,OF⊥BF,又AE=BF,OE=OF
∴△AOE≌△BOF,∴∠AOE=∠BOF
∵CD切半圆于G,∴CF=CG.仿上可得∠COF=∠COG,同理∠DOE=DOG
∵∠AOE+∠DOE+∠DOG+∠COG+∠COF+∠BOF=180°,∴∠AOE+∠DOE+∠COF=90°
∴∠BCO=90°-∠COF=∠AOE+∠DOE=∠AOD
同理∠BOC=∠ADO,∴△BCO∽△AOD,∴BC/AO=BO/AD
设AO=BO=a,则y=![]()
15.B
解:用排除法:从函数图象可以看出:①的支出费用减少,反映了建议(1);③的支出费用没改变,提高了车票价格,反映了建议(2);②、④不符合题意。
故正确答案是B。
16.D
分析:仅从题设所给的条件看,无法直接确定m,n,a,b的大小关系,故本题宜采用排除法。
解:将a、b带入原方程得:3-(a-m)(a-n)=0,3-(b-m)(b-n)=0
故(a-m)(a-n)=(b-m)(b-n)=3>0
根据A、B、C、D四个选项判断(a-m)(a-n)和(b-m)(b-n)的正负,只有D符合。
17.A
方法同上题
18.C
解:方法一
如图1,过C作CE⊥AB于E,过A作FA⊥AB交BC的延长线于F,连结CA、CD
∵AD=5,BD=7,∴AB=12
 ∵∠CDA=∠CBD+∠DCB=
∵∠CDA=∠CBD+∠DCB=![]() =
=![]() =∠CAD
=∠CAD
∴CA=CD,∴AE=![]() AD=
AD=![]() ,∴BE=12-
,∴BE=12-![]() =
=![]()
设BC=x,∵CE⊥AB,FA⊥AB,∴CE∥FA,∴![]() =
=![]()
即![]() =
=![]() ,∴CF=
,∴CF=![]() x,∴BF=x+
x,∴BF=x+![]() x=
x=![]() x
x
由切割线定理得:AF 2=CF·BF=![]() x·
x·![]() x=
x=![]() x 2
x 2
在Rt△ABF中,由勾股定理得:AF 2+AB 2=BF 2
即![]() x 2+144=
x 2+144=![]() x 2,解得x=
x 2,解得x=![]()
方法二:
如图2,过D作DE⊥BC交⊙O于E,连结AC、AE、BE、DE,设AE与BC相交于F
 ∵AD=5,BD=7,∴AB=12
∵AD=5,BD=7,∴AB=12
由折叠的对称性可知BE=BD=7,∠ABC=∠EBC=![]() ∠ABE
∠ABE
∴![]() =
=![]() =
=![]() ,∴EF=
,∴EF=![]() AE
AE
∵AB是⊙O的直径,∴∠AEB=90°
∴AE=![]() =
=![]() =
=![]() ,∴EF=
,∴EF=![]()
∴BF=![]() =
=![]()
∵AB是⊙O的直径,∴∠ACB=90°,∴△ABC∽△FBE,∴![]() =
=![]()
∴BC=![]() ·AB=
·AB=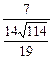 ×12=
×12=![]()
19.A
方法同上
20.B
解:如图,设未知的三块面积分别为x,y,z
则![]()
经消元得:y=85
21.B
分析:这是一道生活中的物流资源调配问题,是对生活中最优化模型的研究,需要用函数的最值加以解决。
解:设A→B的件数为x1(规定:当x1<0时,则B调整了|x1|件给A,下同),B→C的件数为x2,C→D的件数为x3,D→A的件数为x4
由题意得:x4+50-x1=40,x1+50-x2=45,x2+50-x3=54,x3+50-x4=61
从而x2=x1+5,x3=x1+1,x4=x1-10,故调动件次f(x1)=|x1|+|x1+5|+|x1+1|+|x1-10|
画出图像(或绝对值的几何意义)可得最小值为16
22.A
解:如图,AC边从开始到结束所扫过的图形的面积为图中阴影部分的面积S
 S阴影=
S阴影=![]() ×
×![]() ×(
×(![]() )2+S△ABC-
)2+S△ABC-![]() ×
×![]() ×12+
×12+![]() ×
×![]() ×22-
×22-![]() ×
×![]() ×12-S△ABC=
×12-S△ABC=![]()
23.D
解:由题意知AC=2AB=6,AB=AD=CD=3
如图,易知S△ABM=S△ADM=S△CDM=![]() S△ABC=
S△ABC=![]() ×
×![]() ×3×6=3
×3×6=3
 所以点M到AC的距离(即△ADM的AD边上的高)=
所以点M到AC的距离(即△ADM的AD边上的高)=![]() =
=![]() =2
=2
24.C
解:易知三种地砖的内角分别是![]() ,
,![]() ,
,![]()
由题意可得:![]() +
+![]() +
+![]() =360°,从而
=360°,从而![]() =
=![]()
25.D
∵A1B1⊥A2C2,∴由对称性可知B1C1⊥A2B2,C1A1⊥B2C2
∴Rt△A1AF,Rt△A2AB,Rt△B1CB,Rt△B2CD,Rt△C1ED,Rt△C2EF全等
设A1B1=a(a为正整数),AA1=x,则AF=![]() x,A1F=2x,有x+
x,A1F=2x,有x+![]() x+2x=a,解得x=
x+2x=a,解得x=![]() a
a
故S△A1AF=![]() x 2=
x 2=![]() (
(![]() a)2=(
a)2=(![]() -
-![]() )a 2
)a 2
则S=![]() a 2-3S△A1AF=
a 2-3S△A1AF=![]() a 2-3(
a 2-3(![]() -
-![]() )a 2=
)a 2=![]() a 2-
a 2-![]() a 2
a 2
由已知S=![]() -
-![]() 及a为正整数,m、n为有理数,得m=
及a为正整数,m、n为有理数,得m=![]() ,n=
,n=![]()
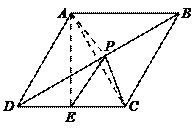 ∴
∴![]() =
=![]()
26.B
解:如图,连结AP、AC、AE
∵菱形ABCD,∠DAB=120°,∴△ADC为等边三角形
∵E为DC中点,∴AE⊥DC
由对称性可知PA=PC,∴PE+PC=PE+PA≥AE=![]() AD=
AD=![]() AB
AB
即![]() AB≤1,∴AB≥
AB≤1,∴AB≥![]()
故边AB长的最大值是![]()
27.A
解:把y=0代入y=x+n,得x=-n,A(-n,0)
把x=0代入y=x+n,得y=n,Q(0,n)
同理可求出点B的坐标为(![]() ,0)
,0)
因为点P是直线y=x+n与直线y=-2x+m的交点,所以点P的坐标是方程组
联立![]() 解得
解得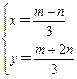 ∴P(
∴P(![]() ,
,![]() )
)
如图,连结PO,则有:
S△POB=![]() ·
·![]() ·
·![]() =
=![]() ,S△POQ=
,S△POQ=![]() ·n·
·n·![]() =
=![]()
由已知S四边形PQOB=S△POB+S△POQ=![]() 及AB=AO+OB=2
及AB=AO+OB=2
得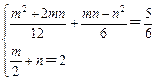 解得n=±1,∵n>0,∴n=1,∴m=2
解得n=±1,∵n>0,∴n=1,∴m=2
∴P(![]() ,
,![]() )
)
28.C
解:如图,2环相扣时,铁链的总长度为:(64+18×2)×2-2×18,即100×2-36×1
3环相扣时,铁链的总长度为(64+18×2)×3-2×18×2,即100×3-36×2
……
n环相扣时,铁链的总长度为:100n-36(n-1)=64n+36
设长14.5米的铁链共有x个环,则:64x+36=14500,解得:x=226
所以共有226个环
29.D
解:设一次函数的解析式为y=kx+b,则3=2k+b,得b=3-2k
令y=0得x=-![]() ,∴OA=-
,∴OA=-![]()
令x=0得y=b,则OB=b
S△AOB=![]() ×(-
×(-![]() )×b=
)×b=![]() ×
×![]() =
=![]() ×
×![]() =
=![]() ×[(
×[(![]() )2+24]≥12
)2+24]≥12
故△AOB面积的最小值为12
30.C
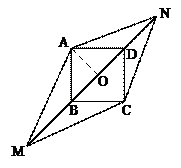 解:设BD中点为O,连结AO,则AO⊥BD,AO=OB=
解:设BD中点为O,连结AO,则AO⊥BD,AO=OB=![]()
MO=![]() =
=![]() ,∴MB=MO-OB=
,∴MB=MO-OB=![]()
又∠ABM=∠ADN=135°,
∠NAD=∠MAN-∠BAD-∠MAB=135°-90°-∠MAB=45°-∠MAB=∠AMB
所以△ADN∽△MBA,故![]() =
=![]() ,从而DN=
,从而DN=![]() ·BA=
·BA=![]() ×1=
×1=![]()
根据对称性可知,四边形AMCN的面积=2S△MAN=2×![]() ×MN×AO
×MN×AO
=2×![]() ×(
×(![]() +
+![]() +
+![]() )×
)×![]() =
=![]()
 31.A
31.A
解:过P作PD⊥AB于D,PE⊥BC于E,设AD=x,DP=y
则![]() 解得
解得![]() 或
或![]()
当x=1,y=2时,点P在△ABC外,不合题意,舍去,∴x=2,y=1
∴DB=5-2=3,∴PB=![]() =
=![]() =
=![]()
32.D
解:∵DE∥FG∥BC,∴△ADE∽△AFG∽△ABC
∴DE 2 : FG 2 : BC 2=S1 : S2 : S3=S1 : 2S1 : 3S1=1 : 2 : 3
∴DE : FG : BC =1
:![]() :
:![]()
设DE=x,则FG=![]() ,BC =
,BC =![]()
∵BC=![]() ,∴
,∴![]() =
=![]() ,∴x=
,∴x=![]()
∴DE=![]() ,FG=2,∴FG -DE=2-
,FG=2,∴FG -DE=2-![]()
 33.D
33.D
解:如图,以AB为一边向△ABC内作等边三角形ABD,连结PD、CD
则AD=BD=AB=AC,∠ABD=∠BAD=60°,∴∠ACD=∠ADC
∴∠DAC=∠BAC-∠BAD=80°-60°=20°,∴∠ACD=∠ADC=80°
∵AB=AC,∠BAC=80°,∴∠ABC=∠ACB=50°
∴∠DBC=60°-50°=10°=∠PBC,∠DCB=80°-50°=30°=∠PCB
又BC=BC,∴△BDC≌△BPC,∴BD=PB,∴AB=PB
∴∠PAB=∠APB=70°
34.B
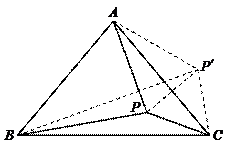 解:如图,作点P关于AC的对称点P′,连结AP′、P′C、PP′,则P′C=PC,ACP′=∠ACP
解:如图,作点P关于AC的对称点P′,连结AP′、P′C、PP′,则P′C=PC,ACP′=∠ACP
∵AB=AC,∠BAC=80°,∴∠ABC=∠ACB=50°
又∠PBC=10°,∠PCB=20°,∴∠BPC=150°,∠ACP=30°,∠ACP′=30°
∴PCP′=60°,∴△PCP′是等边三角形,∴PP′=PC,∠P′AC=∠PAC,∠P′PC=60°
∴∠BPP′=360°-150°-60°=150°,∴∠BPP′=∠BPC
∴△PBP′≌△PBC,∴∠PBP′=∠PBC=10°,∴∠P′BC=20°,∠ABP′=30°
又∠ACP′=30°,∴∠ABP′=∠ACP′
∴A、B、C、P′ 四点共圆,∴∠PAC=∠P′AC=∠P′BC=20°
∴∠PAB=60°
35.C
解:纸片由五个边长为1的小正方形组成,所以纸片的面积为5
过A点剪一刀后,阴影部分面积是纸片面积的一半,故阴影部分面积为![]()
 如图,设EC=x,BE=y,则有
如图,设EC=x,BE=y,则有![]() xy=
xy=![]() ,∴xy=5
,∴xy=5
由△BDA∽△BEC得![]() =
=![]() ,整理得x+y=xy
,整理得x+y=xy
∴x+y=xy=5,∴x 2+y 2=(x+y)2-2xy=5 2-2×5=15
∴BC=![]() =
=![]()
36.B
解:如图,过O作EF⊥AD于E,交BC于F;过O作GH⊥DC于G,交AB于H
设CF=m,FB=n,AH=x,HB=y,则OG=m,OH=n,DG=x,OF=y
由勾股定理得:OF 2=OC 2-CF 2=OB 2-BF 2,即4 2-m 2=3 2-n 2
 ∴m 2-n 2=4 2-3 2=7
①
∴m 2-n 2=4 2-3 2=7
①
同理有OH 2=1 2-x 2=3 2-y 2
∴y 2-x 2=3 2-1 2=8 ②
又OH 2+HB 2=OB 2,即n 2+y 2=9
①-②得(m 2+x 2)-(n 2+y 2)=-1
∴OD 2=m 2+x 2=(n 2+y 2)-1=9-1=8
∴OD=![]()
37.A
解:由a<0可知二次函数的图象开口向下,又当x=1时,y=a+b+c>0,所以函数图象与x轴有两个交点,故选A.
38.C
解:从题目所给的几个数据会发现:25、60、65是勾股数;39、52、65是勾股数,由此可知该圆内接四边形是由具有公共斜边为65的两个直角三角形构成,故选C.
39.A
解:∵DAEF=90°,∴∠CEF+∠AED=90°
又∠CEF+∠EFC=90°,∴∠EFC=∠AED
又∠C=∠D=90°,∴△EFC∽△AED
∴![]() =
=![]() =
=![]() ,∴△AEF∽△BCE,∴∠GAE=∠GBF
,∴△AEF∽△BCE,∴∠GAE=∠GBF
又∠AGE=∠BGF,∴△AGE∽△BGF
∴![]() =
=![]() ,又∠AGB=∠EGF,∴△ABG∽△EFG
,又∠AGB=∠EGF,∴△ABG∽△EFG
∴![]() =
=![]() =
=![]()
设正方形的边长为2,则AE=BE=![]() ,EF=
,EF=![]() ,AF=
,AF=![]()
∴![]() =
=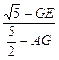 =
=![]() =
=![]() ,解得GE=
,解得GE=![]() ,∴BG=
,∴BG=![]()
∴BG : GE=![]()
40.A
解:① ∵直角梯形ABCD,∴∠ABC=∠A=90°
 又∠DEB=90°,∴四边形ABED是矩形
又∠DEB=90°,∴四边形ABED是矩形
又AB=AD,∴四边形ABED是正方形
∴DE=AD,又∠A=∠DEC=90°,AF=EC,∴△ADF≌△EDC
∴DF=DC,∠ADF=∠EDC
又∠ADF+∠FDE=90°,∴∠EDC+∠FDE=90°
∴∠FDC=90°,∴△DFC是等腰直角三角形
设FC与BD相交于点G,则∠DFG=∠DCF=45°
∵∠CBG=45°,∴∠DFG=∠CBG
又∠FGD=∠BGC,∴△FDG∽△BCG,∠FDB=∠FCB,故①正确
∵∠FDN=45°+∠FDB,∠BCD=45°+∠FCB,∴∠FDN=∠BCD
又∠DFN=∠CBD=45°,∴△DFN∽△DBC,故②正确
连结DM,则DM⊥FC,∠FDM=∠CDM=45°
又∠FDB=45°-∠ADF,∠MDE=45°-∠EDC
∴∠FDB=∠MDE,又DF:DM=DB:DE=![]()
∴△DFB∽△DME,∴FB=![]() ME,故③正确
ME,故③正确
由△DFB∽△DME可知,∠MED=∠FBD=45°
∴MEE是正方形ABED的对角线,∴ME垂直平分BD,故④正确
综上所述,①②③④都正确,故选D.
41.B
解:正方形ABCD的边长为![]() =
=![]()
易证△BCE≌△CDF,∠EBC=∠FCD
∵∠BEC+∠EBC=90°,∴∠BEC+∠FCD=90°
∴∠EHC=90°,∴△EHC∽△ECB
∴S△EHC=![]() ·S△ECB=(
·S△ECB=(![]() )2×
)2×![]() ×240=12
×240=12
易证△GBC∽△GDF,∴S△EHC=![]() ×
×![]() ×240=80
×240=80
∴S四边形DGHE=![]() ×240-12-80=28
×240-12-80=28
42.C
解:过D作DF⊥BC于F
∵ABCD是等腰梯形,∴BE=CF,AD=EF
设AD=a,BE=b,则AE=4a,CF=b,EC=EF+CF=AD+BE=a+b
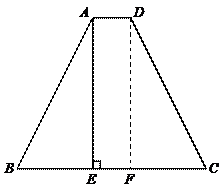 AC=
AC=![]() =
=![]() ,BC=BE+EC=a+2b
,BC=BE+EC=a+2b
∵AC=BC,∴![]() =a+2b
=a+2b
整理得:16a 2-2ab-3b 2=0,解得:a=![]() b,∴BE=2a
b,∴BE=2a
则AB=![]() =
=![]() =
=![]() a
a
又AB=4√5,∴a=2,b=4
∴AD=2,BC=2+2×4=10,AE=4×2=8
∴梯形ABCD的面积=![]() (AD+BC)·AE=
(AD+BC)·AE=![]() (2+10)×8=48
(2+10)×8=48
43.D
解:∵AD、BE、CF是△ABC的三条高,∴B、C、E、F四点共圆
∴△AEF∽△ABC,∴![]() =
=![]() =
=![]() ,即cos∠BAC=
,即cos∠BAC=![]() ,∴sin∠BAC=
,∴sin∠BAC=![]()
在Rt△ABE中,BE=AB·sin∠BAC=6×![]() =
=![]()
44.C
解:∵∠BCE=15°,∴∠BEC=75°,∴∠AEC=105°
∴∠ADC=105°,∴∠BCD=75°,∴∠ECD=60°
又CE=CD,∴△CDE为等边三角形,故①正确
∵∠BEH=∠BEC+∠HEC=75°+60°=135°
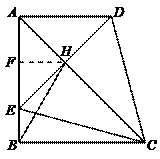 而∠ADC=105°,∴△BEH与△ADC不相似,故②错
而∠ADC=105°,∴△BEH与△ADC不相似,故②错
∵∠EBC=90°,∠EHC=90°,∴B、E、H、C四点共圆
∴∠BHE=∠BCE=15°,∴∠BHC=75°=∠BCD,故③正确
∵∠BEH=135°,∴∠AEH=45°
过H作HF⊥AB于F,则EH=![]() FH
FH
BE=BF-EF=![]() FH-FH=(
FH-FH=(![]() -1)FH
-1)FH
∴EH=![]() =
=![]() BE,故④错
BE,故④错
由折叠的对称性可知∠BAC=∠DAC=45°,又∠ABC=90°
∴AB=BC
又AB=AE+BE=2FH+(![]() -1)FH=(
-1)FH=(![]() +1)FH,∴BC=(
+1)FH,∴BC=(![]() +1)FH
+1)FH
而△BCE的面积=![]() ×BC×BE=
×BC×BE=![]() ×(
×(![]() +1)FH×(
+1)FH×(![]() -1)FH=FH 2
-1)FH=FH 2
△AHE的面积=![]() ×AE×FH=
×AE×FH=![]() ×2FH×FH=FH 2
×2FH×FH=FH 2
∴△BCE的面积=△AHE的面积
又∵四边形BCHE的面积=△BCE的面积+△HCE的面积
=△AHE的面积+△HCE的面积
=△AEC的面积=△ADC的面积
故⑤正确
综上所述,①③⑤正确,②④错误,故选C.

45.B
解:如图,延长CB至点G,使BG=AC,连结OG
∵∠DBG=90°-∠ABC,∠BAC=90°-∠ABC,∴∠DBG=∠BAC
又∠OBG=45°+∠DBG,∠OAC=45°+∠BAC,∴∠OBG=∠OAC
又OB=OA,∴△OBG≌△OAC,∴∠BOG=∠AOC,OG=OC
∴∠COG=∠COB+∠BOG=∠COB+∠AOC=∠AOB=90°
∴△COG是等腰直角三角形,∴CG=![]() OC=8
OC=8
BC=CG-BG=8-3=5.
46.D
解:当k >0时,函数y=k|x|与y=x+k的图象如图1所示
若0<k≤1,则y=k|x|与y=x+k的图象只有一个交点;若k >1,则y=k|x|与y=x+k的图象有两个公共点
当k <0时,函数y=k|x|与y=x+k的图象如图2所示
若-1≤ k <0,则y=k|x|与y=x+k的图象只有一个交点;若k <-1,则y=k|x|与y=x+k的图象有两个公共点
综上所述,实数k的取值范围是k <-1和k >1,故选D.


47.D
解:设AB=x,AB与CD间距离为y,由S△DCF =4知F到CD的距离为![]()
则F到AB的距离为y-![]() ,∴S△BEF =
BE(y - )=3
,∴S△BEF =
BE(y - )=3
∴BE = ,AE = x - =
 S△AED = AE×y= × ×y=5,得(xy)2-24xy+80=0
S△AED = AE×y= × ×y=5,得(xy)2-24xy+80=0
解得xy =20或4
∵SABCD =xy>S△AED =5,∴xy =4不合题意,舍去,∴xy =20
S△DEF =SABCD -S△AED -S△BEF -S△DC F =20-5-3-4=8
48.A
解:易求得抛物线与x轴的交点B、C的坐标分别为B(-2,0),C(4,0),则BC=6
∵y=-x 2+2x+8=-(x-1)2+9,∴抛物线顶点为E(1,9),对称轴为x=1
如图,以BC为直径作⊙D,则⊙D的半径为3
因为直径所对的圆周角为直角,圆外角为锐角,圆内角为钝角
又点A在x轴上方的的抛物线上,故当∠BAC为锐角时,3< AD ≤9.
49.C
解:正方形ABCD在绕点C旋转的过程中,A点的轨迹是以点C为圆心,AC为半径的圆(如图).
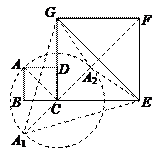 因为△AEG的边EG=
因为△AEG的边EG=![]() ,故当A点到EG的距离取得最大、最小值时,S取得最大、最小值.
,故当A点到EG的距离取得最大、最小值时,S取得最大、最小值.
当A1F⊥EG时,S取得最大值;
S最大=![]() ×
×![]() ×(
×(![]() +
+![]() b)=
b)=![]() b 2+ab
b 2+ab
当A2F⊥EG时,S 取得最小值.
S最小=![]() ×
×![]() ×(
×(![]() b-
b-![]() )=
)=![]() b 2-ab
b 2-ab
 故
故![]() b 2-ab≤ S ≤
b 2-ab≤ S ≤![]() b 2+ab
b 2+ab
50.A
解:如图,由于(35+x+49)+(13+y)=长方形面积的一半=x+S阴影+y
所以S阴影=35+49+13=97
51.B
 解:∵AD、BE分别是△ABC的BC、AC边上的中线,∴AE=
解:∵AD、BE分别是△ABC的BC、AC边上的中线,∴AE=![]() ,BD=
,BD=![]()
设OD=x,OE=y
则由三角形中线的性质可知OA=2x,OB=2y
∵AD⊥BE,∴△AOB、△AOE和△BOD都是直角三角形
由勾股定理得:OA 2+OE 2=AE 2,OB 2+OD 2=BD 2
即4x 2+y 2=20,4y 2+x 2=![]() ,两式相加得:5x 2+5y 2=
,两式相加得:5x 2+5y 2=![]()
∴x 2+y 2=![]() ,∴AB 2=OA 2+OB2=4x 2+4y 2=25,∴AB=5
,∴AB 2=OA 2+OB2=4x 2+4y 2=25,∴AB=5
52.C
解:考虑到如果求出该正方形在第一象限面积的精确值,则必须先利用相似三角形求出FH、EG的长度,再计算面积,这样的话,计算过程相当复杂,还容易出错。如果先粗略估算,然后用排除法,则简便得多。
如图,过A作AE⊥x轴于E,过B作BF⊥x轴于F,设AD、BC分别交x轴于G、H,则AE=6,BF=3,EF=6+4=10
该正方形在第一象限的面积=梯形ABFE的面积-△BFH的面积+△AEG的面积
=![]() ×(3+6)×10-△BFH的面积+△AEG的面积
×(3+6)×10-△BFH的面积+△AEG的面积
=45-△BFH的面积+△AEG的面积
显然△AEG的面积大于△BFH的面积,所以该正方形在第一象限的面积大于45,而A、B、C、D四个选项中只有C符合,故选C.
53.D
解:由勾股定理得AC=![]() =
=![]() =5,由三角形的面积可求得A1B=
=5,由三角形的面积可求得A1B=![]()
∵所有的直角三角形都是相似三角形
∴Rt△A1B1B的面积
: Rt△A1AB的面积=A1B 2 : AB 2=(![]() )2 : 3 2=
)2 : 3 2=![]()
从而Rt△A1B1B的面积
: 直角梯形A1ABB1的面积=![]()
叠加得所有阴影三角形的面积之和
: Rt△ABC的面积=![]()
故所有阴影三角形的面积之和=![]() ×
×![]() ×3×4=
×3×4=![]()
54.D
解:如图,过C作CG∥BD交AD的延长线于G,则△CDG≌△BDE,△AEF∽△AGC
 ∴BE=GC,DG=ED=2AE,∴AG=5AE
∴BE=GC,DG=ED=2AE,∴AG=5AE
∵AE : ED=1 : 2,∴△CDG的面积=△BDE的面积=![]() =8
=8
∴△AGC的面积=8+![]() ×24=20
×24=20
∴△AEF的面积=![]() ×20=
×20=![]()
55.A
 解:延长AG交BC于D,延长GD至E,使DE=GD
解:延长AG交BC于D,延长GD至E,使DE=GD
∵点G是△ABC的重心,∴BD=DC,GA=2GD=GE=4,AD=![]() GA=6
GA=6
又∵DE=GD,∴四边形BECG是平行四边形
∴CE=GB=5,S△GEB=S△GEC
又∵GE=4,GC=3,∴△GEC是直角三角形,∴△AGC是直角三角形
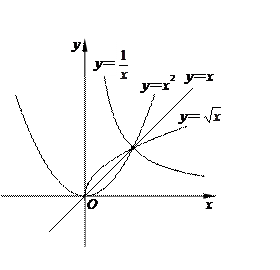 ∴S△ABC=2S△ADC=2×
∴S△ABC=2S△ADC=2×![]() S△GAC=3S△GAC=3×
S△GAC=3S△GAC=3×![]() ×4×3=18
×4×3=18
56.A
解:方法一
∵0< x <1,∴x 2 <x <1,![]() >1,∴x <
>1,∴x <![]() <1,
<1,
∴x 2 <x <![]() <
<![]()
方法二
在同一坐标系中画出这四个函数的图象,如图
从函数图象可以看出:当0< x <1时,x 2<x<![]() <
<![]()
 57.C
57.C
解:连结FC,则S△DCF =![]() S△BDF ,S△CEF =
S△BDF ,S△CEF =![]() S△AEF
S△AEF
∴S四边形DCEF =S△DCF +S△CEF =![]() ( S△BDF +S△AEF )=
( S△BDF +S△AEF )=![]() ( S△BCE +S△ADC -2S四边形DCEF )
( S△BCE +S△ADC -2S四边形DCEF )
∴S四边形DCEF =![]() ( S△BCE +S△ADC )=
( S△BCE +S△ADC )=![]() ×
×![]() S△ABC =
S△ABC =![]() ×
×![]() ×6=1
×6=1
58.B
解:若x+3=0,则x=-3;
若x 2+x-1=1,则x=-2或x=1;
若x 2+x-1=-1则x=0或x=-1,当x=0时,x+3=3,(-1)3=-1,不合题意,舍去;当x=-1时,x+3=2,(-1)2=1,符合题意
所以原方程的整数解是-3,-2,-1,1,共4个,故选B.
59.D
解:如图,过C作CG∥AD交BE的延长线于G,则△ECG≌△AOE,△BDO∽△BCG
∴AO=GC,EG=OE=BO,∴BG=3BO
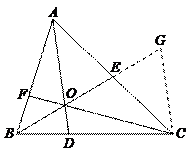 ∴S△ECG =S△AOE =
∴S△ECG =S△AOE =![]() S△ABE =
S△ABE =![]() S△ABC =
S△ABC =![]()
∴S△BCG =S△BCE +S△ECG=![]() +
+![]() =
=![]()
∴S△BDO =![]() ×S△BCG =
×S△BCG =![]() ×
×![]() =
=![]()
同理可得S△BFO =![]()
∴S四边形BDOF =S△BDO+S△BFO =![]() +
+![]() =
=![]()
60.D
解:∵2x 2-5mx+2m 2=5,∴(2x-m)(x-2m )=5
∵x,m均为整数,∴2x-m与x-2m也为整数
∴![]() 或
或![]() 或
或![]() 或
或![]()
解得![]() 或
或![]() 或
或![]() 或
或![]()
所以整数的整数m的值共有4个.
61.C
解:
设⊙O1的半径为3x,⊙O2的半径3y,则O1B=5x,O2D=5y
BD=O1B+O1O2+O2D=8(x+y)=5,∴x+y=![]()
∴O1O2=3(x+y)=![]()
62.解:由函数图象可得a<0,b>0,c=0
∴p=|a-b|+|2a+b|,q=|a+b|+|2a-b|
又-![]() >1,∴-b<2a,∴ a-b<0,2a-b<0,2a+b>0,∴a+b>-a>0
>1,∴-b<2a,∴ a-b<0,2a-b<0,2a+b>0,∴a+b>-a>0
 ∴p=b-a+2a+b=2b+a,q=a+b+b-2a=2b-a
∴p=b-a+2a+b=2b+a,q=a+b+b-2a=2b-a
∴p<q,故选C.
63.A
解:如图,过E作EH⊥AB于H,交AC于F,则EH=![]() ,FH=AH=
,FH=AH=![]()
∴EF=![]() ,S阴影=
,S阴影=![]() ×EF×AB=
×EF×AB=![]()
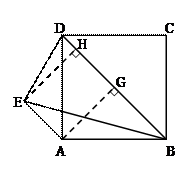
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰DC绕点D的逆时针方向旋转90°至DE,连结AE,则△ADE的面积是( ) C
A.1 B.2 C.3 D.4
64.D
解:连结OD、OE
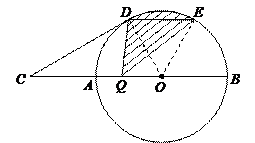 ∵DE∥CB,∴S△QDE=S△ODE,∴S阴影=S扇形ODE
∵DE∥CB,∴S△QDE=S△ODE,∴S阴影=S扇形ODE
设圆的半径为r,由切割线定理,CD 2=CA·CB=CA·(CA+AB)
即(![]() )2=1×(1+2r),解得r=1
)2=1×(1+2r),解得r=1
又CD=![]() AB=
AB=![]() r,∴∠COD=60°
r,∴∠COD=60°
∵DE∥CB,∴∠ODE=60°,∴△ODE是等边三角形
∴S阴影=![]() ×12×
×12×![]() =
=![]()
65.B
解:设半圆O的半径为r,S扇形AOC =![]() ×
×![]() ×r2=
×r2=![]() r2=
r2=![]() r2,S△COB =
r2,S△COB =![]() ×r×
×r×![]() r=
r=![]() r2
r2
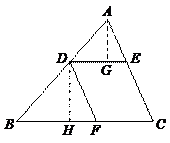 S弓形BmC =S扇形COB -S△COB =
S弓形BmC =S扇形COB -S△COB =![]() r2-
r2-![]() r2=
r2=![]() r2
r2
∴S2<S1<S3
66.C
解:如图,过A作AG⊥DE于G,过D作DH⊥BC于H
则S△ADE =![]() DE·AG=1,S△DBF =
DE·AG=1,S△DBF =![]() BF·DH=2
BF·DH=2
由△ADE∽△DBF得S△ADE : S△DBF =DE 2 : BF 2=AG 2 : DH 2=1 : 2
设DE=x,则AG=![]() ,DH=AG=
,DH=AG=![]()
S四边形DECF =DE·DH=x·![]() =
=![]()
67.C
解:分别是△DPC、△BCQ、△ADQ、△DBP和△BQD
68.D
解:因为相似三角形的面积比等于相似比的平方,所以底边相似比分别为3 : 4 : 8
设△1、△2、△3底边分别为3x,4x,8x,则BC=15x,所以△ABC的面积是225
69.A
解:∵AD∥BC,∴S△ABD =S△ACD ,∴S△AOB =S△COD
又∵S△AOB : S△AOD =OB : OD=S△AOB : 4,S△BOC : S△COD =OB : OD=16 : S△AOB
∴S△AOB : 4=16 : S△AOB ,∴S△AOB=S△COD=8
∴S梯形ABCD=4+8+16+8=36
70.C
解:①③④正确,②错
71.C
解:如图,连结OE、OF
易证△OBF是等边三角形,BC=6,BF=4,CD=![]() ,CE=
,CE=![]()
阴影部分的面积S=S梯形OBCE-S扇形OFE-S△OBF+S扇形OBF-S△OBF=S梯形OBCE-2S△OBF
=![]() ×(4+6)×
×(4+6)×![]() -2×
-2×![]() ×4 2=
×4 2=![]()
72.B
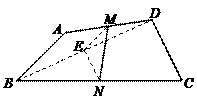 解:如图,连结BD,取BD的中点E,连结EM、EN,则
解:如图,连结BD,取BD的中点E,连结EM、EN,则
EM+EN>MN,即![]() AB+
AB+![]() CD>MN,AB>MN
CD>MN,AB>MN
73.A
解:由题意,显然a >0,当a >0时,a值越大,抛物线开口越小
设正方形的四个顶点为A、B、C、D(如图),显然抛物线经过A(1,2)和C(2,1)时,分别得到a的最大值和最小值
把x=1,y=2代入y=ax 2,得a=2;把x=2,y=1代入y=ax 2,得a=![]() ,故
,故![]() ≤ a ≤2
≤ a ≤2
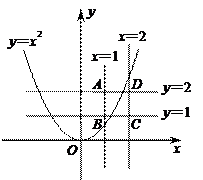
74.D
解:如图,作点N关于AC的对称点N ′,则PM+PN=PM+PN ′
当M、P、N ′三点在同一直线上时,PM+PN ′最小,即PM+PN最小
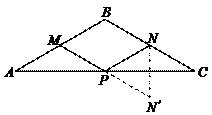 此时∠APM=∠CPN ′=∠CPN,又∠A=∠C,AM=CN,所以△APM≌△CPN
此时∠APM=∠CPN ′=∠CPN,又∠A=∠C,AM=CN,所以△APM≌△CPN
∴PM=PN,AP=CP,P是AC的中点
∴AB=2PN=PM+PN=2,△ABC的周长=4+![]()
75.B
解:如图,延长BA至F,使BF=AC,连结OF
∵∠EBF=90°-∠ABC,∠BCA=90°-∠ABC,∴∠EBF=∠BCA
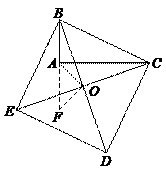 又∠FBO=45°-∠EBF,∠ACO=45°-∠BCA,∴∠FBO=∠ACO
又∠FBO=45°-∠EBF,∠ACO=45°-∠BCA,∴∠FBO=∠ACO
又OB=OC,∴△FBO≌△ACO,∴∠BFO=∠CAO,OF=OA
∴∠BFO+∠FAO=∠CAO+∠FAO=90°,∴∠AOF=90°
∴△AOF是等腰直角三角形,∴AF=![]() AO=4
AO=4
AC=BF=AB+AF=4+4=8
76.A
⊙O从与AC边相切于C点滚动到与BC边相切于C点,转过120°,则⊙O在三个顶点共转过360°,即一圈,又因为在三边上各转过一圈,所以⊙O共转了4圈.
77.D
解:显然,要使△ABP、△APD、△CDP两两相似,∠APD必须为直角
所以点P在以AD为直径的圆上,即点P到AD的距离不大于AD的一半
∴b≤![]() ,故a ≥2b
,故a ≥2b
78.B
解:由题意得:
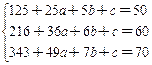 解得a=-18,b=117,c=-210
解得a=-18,b=117,c=-210
∴y=x 3-18x 2+117x-210,把x=4代入,得y=34
79.B
解:设A(x1,0),B(x2,0),则x1+x2=-![]() ,x1x2=
,x1x2=![]() ①
①
∵AQ⊥BQ,∴△ABC为直角三角形,且AB为斜边
∴AQ 2+BQ 2=AB 2,即(x1-n)2+4+(x2-n)2+4=(x1-x2)2
整理得x1x2-n(x1+x2)+n2+4=0
将①代入并整理得:an 2+bn+c+4a=0 ②
又∵点Q(n,2)在抛物线上,∴an 2+bn+c=2
∴2+4a=0,∴a=-![]()
80.A
解:由已知意得a=(b+c)t,b=(c+a)t,c=(a+b)t,∴a+b+c=2(a+b+c)t
当a+b+c≠0时,t=![]() ,∴y=
,∴y=![]() x+
x+![]() ,其图象经过第一、二、三象限
,其图象经过第一、二、三象限
当a+b+c=0时,t=-1,∴y=-x+1,其图象经过第一、二、四象限
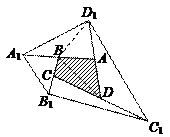 综上所述,一次函数y=tx+t 2的图象必定经过的象限是第一、二象限.
综上所述,一次函数y=tx+t 2的图象必定经过的象限是第一、二象限.
81.D
解:如图,连结BD、BD1,则S△AA1D=2S△ABD1=2S△ABD
同理S△CC1B1=2S△CBD,∴S△AA1D+S△DD1C1=2S
S△BB1A1=2S△ABC,S△DD1C1=2S△ADC,∴S△BB1A1+S△DD1C1=2S
∴四边形A1B1C1D1的面积=S△AA1D1+S△BB1A1+S△CC1B1+S△DD1C1+S四边形ABCD=5S
82.A
解:由△CPE∽△CBA,得![]() =
=![]() ,∴PE=
,∴PE=![]() ·AB=
·AB=![]()
EF=2PE=![]()
83.D
解:如图,过点A作AO∥DG交于BC于点O
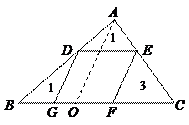 则
则![]() =
=![]() =
=![]() =
=![]()
得S△AOB=![]() S△ABC ,∴S△AOC =
S△ABC ,∴S△AOC =![]() S△ABC
S△ABC
又![]() =
=![]() ①
①
![]() =
=![]() =
=![]() =
=![]()
即![]() =
=![]() =
=![]() ②
②
①+②得: =1
=1
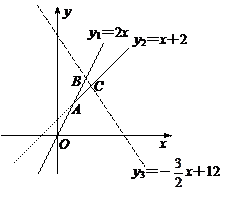 解得S△ABC =9,故S□DEFG =9-(1+3+1)=4
解得S△ABC =9,故S□DEFG =9-(1+3+1)=4
84.C
解:∵|x-x 2|≥0,∴y=1-|x-x 2|≤1
当x-x 2=0,即x=0或x=1时,函数y=1-|x-x 2|有最大值1,
又当x≤0时,y=-x 2+x+1;
当0<x<1时,x 2<x,y=x 2-x+1;
当x≥1时,x 2>x,y=-x 2+x+1
故选C
85.A
解:同上题
86.B
解:分别联立y1、y2,y1、y3,y2、y3得交点A(2,4),B(![]() ,
,![]() ),C(4,6)
),C(4,6)
画出三个函数的图象,如图所示
当x≤2时,min{y1,y2,y3}=y1=2x≤4,最大值为4;
当2<x≤![]() 时,min{y1,y2,y3}=y2=x+2≤
时,min{y1,y2,y3}=y2=x+2≤![]() ,最大值为
,最大值为![]() ;
;
当![]() <x≤4时,min{y1,y2,y3}=y2=x+2≤6,最大值为6
<x≤4时,min{y1,y2,y3}=y2=x+2≤6,最大值为6
当x>4时,min{y1,y2,y3}=y3=-![]() x+12<6
x+12<6
综上,函数y的最大值为6
87.B
解:如图,连结OB,则OB=![]() ,∠AOD=75°,∴∠COD=15°,∴∠BOD=30°
,∠AOD=75°,∴∠COD=15°,∴∠BOD=30°
 ∴点B的纵坐标为-
∴点B的纵坐标为-![]() ,点B的横坐标为
,点B的横坐标为![]() ,∴B(
,∴B(![]() ,-
,-![]() )
)
把点B的坐标代入y=ax 2,解得a=-![]()
故该抛物线的解析式为y=-![]() x 2
x 2
88.C
 解:设此圆的半径为r,圆心为O,连结OA、OB、OC、OD,则有:
解:设此圆的半径为r,圆心为O,连结OA、OB、OC、OD,则有:
r 2=(![]() -2)2+(
-2)2+(![]() )2或r 2=(
)2或r 2=(![]() -3)2+(
-3)2+(![]() )2
)2
∴r =![]()
故此圆的直径D=2r =![]()
89.B
解:如图,延长CP交OY于点D,易知BD=PB=OA,则OA+OB=OB+BD=OD=![]() OC
OC
 故OA+OB+OC=(
故OA+OB+OC=(![]() +1)OC=1,∴OC=
+1)OC=1,∴OC=![]() -1
-1
90.D
解:点P在AD边上的运动时间为12/1=12(秒),点Q在BC边上的运动时间为12/4=3(秒)
所以点P从A运动到D时,点Q在BC边上共运动了4次,每一次都能使线段PQ平行于AB一次,故线段PQ有4次平行于AB
91.C
解:易证Rt△CDF≌Rt△CBE,则CF=CE
∵Rt△CEF的面积是200,即![]() CE·CF=200,∴CE=20
CE·CF=200,∴CE=20
又S正方形ABCD =BC 2=256,∴BC=16
由勾股定理得BE=![]() =
=![]() =12
=12
92.B
解:设等腰直角三角形的直角边长为a,面积为S,则S1=![]() S,S2=
S,S2=![]() S
S
 将图3拼成一个大的等腰直角三角形,如图所示,显然S3=S4
将图3拼成一个大的等腰直角三角形,如图所示,显然S3=S4
设图4中的内切圆的半径为r,由三角形的面积可求得r=![]()
则S3=S4=π[![]() ]2=π
]2=π![]() =(3-
=(3-![]() )πS
)πS
∵![]() <
<![]() <(3-
<(3-![]() )π,∴S2最小
)π,∴S2最小
93.B
解:∵![]() =
=![]() ,∴
,∴![]() =
=![]()
∵BD=c,∴![]() =
=![]()
又∠C=∠C,∴△ABC∽△DAC,∴∠CAB=∠D
又BD=BA=c,∴∠BAD=∠D
∴∠CBA=2∠D,∴∠CBA=2∠CAB
94.B
解:∵f(p)<f(q),∴p 2+λp<q 2+λq,即( p+q )( p-q )+λ( p-q )<0
∴( p-q )( p+q +λ )<0
∵p < q,∴p+q +λ >0,即λ >-( p+q )
同理可得λ >-( q+r),λ >-( p+r)
∵p < q <r,∴-( q+r)<-( p+r)<-( p+q )
∴λ >-( p+q )
∵p、q均为正整数,∴p最小为1,q为2
∴λ >-3
95.B
解:设点D的坐标为(x1,y1),则S1=![]() (-x1)y1=
(-x1)y1=![]() (-x1)
(-x1)![]() =-
=-![]()
易知对于双曲线y=![]() (k<0)上的任一点,S=-
(k<0)上的任一点,S=-![]() 都成立
都成立
∵点P在双曲线的上方,点Q在双曲线的下方,∴S3<S1<S2
96.D
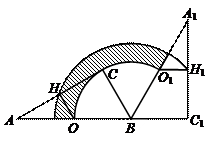 解:如图,连结HB,易求得HB=
解:如图,连结HB,易求得HB=![]() ,OB=2
,OB=2
S阴影=![]() ×
×![]() ×[(
×[(![]() )2-2 2]=π
)2-2 2]=π
97.A
解:由题意知抛物线开口向上,∠ACB=90°,当C点为抛物线的顶点时,BC边上的高取得最大值1
如图,由抛物线的对称性可知,此时AC=BC,△ABC为等腰直角三角形,所以AB=2
 故△ABC面积的最大值为
故△ABC面积的最大值为![]() ×2×1=1
×2×1=1
98.B
解:如图,连结OB、OC,过O作OD⊥BC于D
则∠OBA=90°,OB=1,又OA=2,∴∠BOA=60°
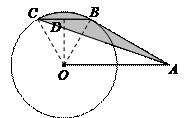 ∵BC∥OA,OD⊥BC,∴∠BOD=∠COD=30°,∴∠BOC=60°
∵BC∥OA,OD⊥BC,∴∠BOD=∠COD=30°,∴∠BOC=60°
∵△ABC与△BOC等底等高,∴S△ABC =S△BOC
∴S阴影=S扇形BOC =![]() ×
×![]() ×1 2=
×1 2=![]()
99.A
解:∵DE是中位线,∴折叠后B、C、A′ 三点在同一直线上
∵∠C=120°,∠A=26°,∴∠B=34°
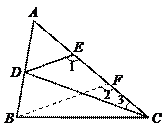 ∵DE是中位线,∴A′D=AD=BD,∴∠A′DB=180°-2×34°=112°
∵DE是中位线,∴A′D=AD=BD,∴∠A′DB=180°-2×34°=112°
100.D
解:∠EDB=180°-82°=98°,∠B=![]() [180°-(98°+30°)]=78°
[180°-(98°+30°)]=78°
101.B
解:如图,由已知,△ADE是等边三角形,作BF∥DE交AC于F,则BD=EF,DE=AD
从而EC=DB+DE=DB+AD=AB=BF,DE=FC
又∠1=∠2=120○,故△EDC≌△FCB,∴∠CDE=∠BCF=∠3+∠DCB
∵∠CDB=2∠CDE,∠BDE=120○,∴∠CDE=40○
∴∠3=180○-120○-40○=20○
∴∠DCB=∠BCF-∠3=40○-20○=20○
 102.D
102.D
解:如图,∵扇形的弧长=圆形的周长,∴![]() πR=2πr,∴R=4r
πR=2πr,∴R=4r
103.A
 解:如图,作∠ACB的平分线CD交AB于D,延长CB至E,使BE=BD,连结DE
解:如图,作∠ACB的平分线CD交AB于D,延长CB至E,使BE=BD,连结DE
设∠A=x,则∠ABC=2x,∠ACD=∠BCD=2x
∴CD=BD=BE,∴∠BDE=∠E=x,∠ADC=∠EDC=4x
∴△ACD≌△ECD,∴AC=CE=b
由△ACD∽△ABC得![]() =
=![]()
∴![]() +
+![]() =
=![]() +
+![]() =
=![]() +
+![]() =
=![]() =
=![]() =
=![]() =1
=1
即![]() +
+![]() =1,∴
=1,∴![]() +
+![]() =
=![]()
104.A
解:如图,连结OP,则OP=OC=1,∴∠OPC=∠OCP
又OCP=∠PCD,∴∠OPC=∠PCD,∴OP∥CD
∵CD⊥AB,∴OP⊥AB,∴∠AOP=90°
∴△AOP是等腰直角三角形,∴AP=![]() ,即y=
,即y=![]()
易知0<x<1,故应选A
105.A
∵对于函数y=ax 2+bx+c,当y>0时,-![]() <x <
<x <![]() ,∴a <0,c >0,其图象开口向下
,∴a <0,c >0,其图象开口向下
并且其对称轴为x=-![]() <0,∴b <0
<0,∴b <0
∴函数y=cx 2-bx+a的图象开口向上,并且其对称轴为x=![]() <0
<0
故正确选项为A
106.D
解:∠AEP=![]() ∠AEB=
∠AEB=![]() [(180°-(∠A+∠ABE)]=90°-
[(180°-(∠A+∠ABE)]=90°-![]() (∠A+∠ABE)
(∠A+∠ABE)
同理∠AFP=90°-![]() (∠A+∠ADF)
(∠A+∠ADF)
∴∠EPF=∠A+∠AEP+∠AFP=180°-![]() (∠ABE+∠ADF)
(∠ABE+∠ADF)
=180°-![]() [360°-(∠A+∠BCD)]=180°-
[360°-(∠A+∠BCD)]=180°-![]() [360°-(60°+124°)]=92°,故A对
[360°-(60°+124°)]=92°,故A对
∠ABC+∠ADC=360°-(∠A+∠BCD)=360°-(60°+124°)=176°,故B对
∠PEB+∠PFD+∠EPF=∠A+∠AEB+∠AFD
 =180°-∠ABE+180°-(∠A+∠ADF)=360°-(∠A+∠ABE++∠ADF)
=180°-∠ABE+180°-(∠A+∠ADF)=360°-(∠A+∠ABE++∠ADF)
=∠BCD=124°,故C对
∠PEB+∠PFD=124°-∠EPF=124°-92°=32°,故D对
107.C
解:如图,延长BA至D,使AD=AC,连结DC
则∠ACD=∠D,∴∠BAC=2∠D
又∠BAC=2∠ACB,∴∠D=∠ACB
又∠B=∠B,∴△CBD∽△ABC
∴![]() =
=![]() ,即
,即![]() =
=![]()
∴BC=![]()
108.B
解:如图,设△ABC的最大角是∠A,最小角是∠C,延长BA至D,使AD=AC,连结DC
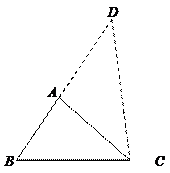 则∠ACD=∠D,∴∠BAC=2∠D
则∠ACD=∠D,∴∠BAC=2∠D
又∠BAC=2∠ACB,∴∠D=∠ACB
又∠B=∠B,∴△CBD∽△ABC
∴![]() =
=![]() ,即
,即![]() =
=![]()
∴BC 2=AB(AB+AC)
∵AB、AC、BC是三个连续的自然数
∴设AB=n-1,AC=n,BC=n+1(n为大于1的正整数)
则(n+1)2=(n-1)(2n-1)
整理得:n 2-5n=0,解得n=0(舍去)或n=5
∴AB=5-1=4
故△ABC的最小边长等于4
109.A
 解:由已知条件可得函数图象如图所示
解:由已知条件可得函数图象如图所示
1)当x=-2时,y=0,∴4a-2b+c=0,故①正确
2)图象的对称轴为x=-![]() <0,∴a,b同号,而a <0,∴b <0
<0,∴a,b同号,而a <0,∴b <0
对称轴为x=![]() =-1+
=-1+![]() ,∵1<x1<2,∴
,∵1<x1<2,∴![]() <
<![]() <1
<1
∴-![]() <-1+
<-1+![]() <0,即-
<0,即-![]() <-
<-![]() <0
<0
∴a <b<0,故②正确
3)∵-2与x1是方程ax 2+bx+c=0的两个根,∴-2x1=![]()
而-4<-2x1<-2,∴-4<![]() <-2
<-2
∴2a+c>0,故③正确
4)∵4a-2b+c=0,∴2(2a-b)+c=0,得2a-b=-![]()
∵函数图象与y轴正半轴的交点在(0,2)的下方,∴0<c<2
∴-1<-![]() <0,即-1<2a-b<0
<0,即-1<2a-b<0
∴2a-b+1>0,故④正确
综上所述,①、②、③、④都正确,故选A
110.C
解:由函数图象可得a>0,c<0
又0<-![]() <1,∴b<0,-2a <b<0,∴2a+b>0,2a-b>0,且|2a+b|<|2a-b|
<1,∴b<0,-2a <b<0,∴2a+b>0,2a-b>0,且|2a+b|<|2a-b|
由函数图象可得:当x=1时,y=a+b+c<0;当x=-1时,y=a-b+c>0
且|a+b+c|<|a-b+c|
∴M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b|<0
故选C.
111.B
解:点F是△ABC的重心,∴AF=![]() AD
AD
∴S△AEF =![]() S△AED =
S△AED =![]() ×
×![]() S△ABD =
S△ABD =![]() ×
×![]() ×
×![]() S△ABC =
S△ABC =![]() S△ABC =10
S△ABC =10
112.D
解:由题意得x1+x2=-1,则x2=-1-x1,且x 12+x1=3
∴x13-4x22+19=x13-4(-1-x1)2+19
=x13-4x 12-8x 1+15
=x 1(x 12+x1)-5x 12-8x 1+15
=-5x 12-5x 1+15
=-5(x 12+x1)+15
=-5×3+15
=0
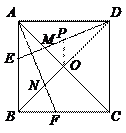 113.D
113.D
解:∵AF平分∠BAC,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,即y=z=
,即y=z=![]()
又△AEM的角分线与高重合,所以△AEM为等腰三角形,AE=AM
如图,过O作OP∥AB,交DE于P,则OP为△DBE的中位线
△OPM∽△AEM,∴x=![]() =
=![]() =2,所以x>y=z
=2,所以x>y=z
114.C
∵a>h>0,b>h>0,∴ab>h 2,a 2+b 2>h 2+h 2=2h 2,故A、D不正确
设斜边为c,则有a+b>c,![]() (a+b)h >
(a+b)h >![]() ch=
ch=![]() ab
ab
∴![]() >
>![]() ,故B不正确
,故B不正确
由![]() h=
h=![]() ab化简整理后,得
ab化简整理后,得![]() =
=![]() ,故C正确
,故C正确
115.C
解:1)∵∠PAE+∠BAQ=180°-90°=90°,∠PAE+∠PEA=90°,∴∠PEA=∠BAQ
又∵∠APE=∠BQA=90°,∴△PAE∽△QBA,∴![]() =
=![]()
∵AQ=PA,∴![]() =
=![]()
又∵∠APE=∠BAE=90°,∴△PAE∽△ABE,故①正确
2)∵△PAE∽△QBA,△PAE∽△ABE,∴△QBA∽△ABE
∴∠QBA=∠ABE,∴3∠ABE=90°
∴∠ABE=30°,故②正确
3)∵∠ABE=30°,∴∠QBA=30°
∴BQ=![]() AB,又∵PA=
AB,又∵PA=![]() PQ=
PQ=![]() AB
AB
∴S△PAE : S△QBA : S△ABE =PA 2 : BQ 2 : AB 2=(![]() AB) 2 : (
AB) 2 : (![]() AB) 2 : AB 2 =1
: 3 : 4,故③正确
AB) 2 : AB 2 =1
: 3 : 4,故③正确
4)∵△PAE∽△ABE,∴∠PEA=∠BEA
∴若沿直线EA折叠纸片,点B落在直线ED上,但不一定与点D重合,只有当BE=DE时,点B才与点D重合,故④错
综上所述,①、②、③选项正确,故选C
116.D
 解:如图,过A作AH⊥BE于H,交BC于O,连结EC
解:如图,过A作AH⊥BE于H,交BC于O,连结EC
则∠BEC=90°,∴AO∥EC
由切线长定理可知AB=AE,∴BH=HE
∴BO=OC=1
∵∠ABH+∠CBE=90°,∠ABH+∠BAO=90°,∴∠CBE=∠BAO
∴sin∠CBE=sin∠BAO=![]() =
=![]() =
=![]()
117.C
解:如图,过B作BG∥AC交CD的延长线于G,则△BDG≌△ADC,△BFG∽△EFC
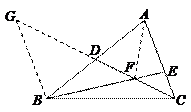 ∴BG=AC=3EC,GD=CD,∴BF=3EF,GF=3CF
∴BG=AC=3EC,GD=CD,∴BF=3EF,GF=3CF
∴CD+DF=3(CD-DF),∴DF=![]() CD
CD
∴S△CEF =![]() S△BCF =
S△BCF =![]() ,S△BDF =S△BCF =1
,S△BDF =S△BCF =1
连结AF,则S△ABF =2S△BDF =2,S△ACF =3S△CEF =1
∴S△ABC =S△ABF +S△BCF +S△ACF =2+1+1=4
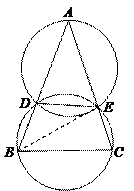
118.B
解:如图,连接BE,∵△ABC为锐角三角形,∴∠BAC,∠ABE均为锐角
又∵⊙O的半径与△ADE的外接圆的半径相等,且DE为两圆的公共弦
∴∠BAC=∠ABE,∴∠BEC=2∠BAC
若△ABC的外心为⊙O1,则∠BO1C=2∠BAC,∴⊙O一定经过△ABC的外心
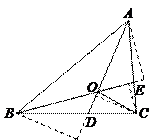 119.D
119.D
解:如图,分别作△AOB的OB边上的高,△BOC的OB边上的高,△AOB的
OA边上的高,△AOC的OA边上的高
则S△BOC : S△AOB=CE : AE=1 : 2=3 : 6,S△AOC : S△AOB=CD : BD=2 : 3=4 : 6
∴S△BOC : S△AOC : S△AOB=3 : 4 : 6
120.C
解:把原方程变形为2[x]=x 2-3
∵x≥[x],∴2x≥x 2-3
解此不等式得:-1≤x≤3
1)当-1≤x<0时,[x]=-1
原方程化为x 2-1=0,解得x=-1(x=1不合题意,舍去)
2)当0≤x<1时,则[x]=0
原方程化为x 2-3=0,解得x=±![]() (不合题意,舍去)
(不合题意,舍去)
3)当1≤x<2时,[x]=1
原方程化为x 2-5=0,解得x=±![]() (不合题意,舍去)
(不合题意,舍去)
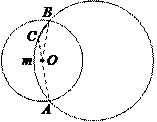 4)当2≤x<3时,[x]=2
4)当2≤x<3时,[x]=2
原方程化为x 2-7=0,解得x=![]() (x=-
(x=-![]() 不合题意,舍去)
不合题意,舍去)
5)当x≥3时,[x]=3
原方程化为x 2-9=0,解得x=3(x=-3不合题意,舍去)
综上所述,方程x 2-2[x]-3=0的解为-1,-![]() ,3,共3个
,3,共3个
121.A
解:易知,小圆的圆心O必在两圆的重叠区域内,连结OA、OB,并延长AO交大圆于点C
则AC+BC=OA+OC+BC >OA+OB=d
又 >AC+BC,∴ >d
122.C
解:把(2,1)代入y=![]() ,得k=2,∴y=
,得k=2,∴y=![]()
当x=-2时,y=-1;当x=1时,y=2
把(-2,-1)(1,2)分别代入y=ax 2,解得a=-和a=2
对于二次函数y=ax 2,当a <0时,a越大,抛物线开口越大;当a >0时,a越小,抛物线开口越大
∵二次函数y=ax 2与上述图象有公共点,∴-≤ a ≤2且a≠0
推荐内容
教育新鲜事


 初中生必须吃透的28个数
初中生必须吃透的28个数 初中数学 | 三角形知识
初中数学 | 三角形知识 中考数学最易出错的61个
中考数学最易出错的61个 中考数学选填压轴题专题
中考数学选填压轴题专题