初中数学巧添辅助线，解证几何倍角关系

在初中数学阶段，我们经常会遇到一些几何证明和计算题，而在几何证明或计算问题中，经常需要添加必要的辅助线，它的目的可以归纳为以下三点：一是通过添加辅助线，使图形的性质由隐蔽得以显现，从而利用有关性质去解题；二是通过添加辅助线，使分散的条件得以集中，从而利用它们的相互关系解题；三是把新问题转化为已经解决过的旧问题加以解决。值得注意的是辅助线的添加目的与已知条件和所求结论有关。

下面我们一起来看看深本数学的老师如何解析倍角关系的几何题。

分析：∠DBC、∠BAC所在的两个三角形有公共角∠C，可利用三角形内角和来沟通∠DBC、∠BAC和∠C的关系。

分析二：∠DBC、∠BAC分别在直角三角形和等腰三角形中，由所证的结论“∠DBC= ?∠BAC”中含有角的倍、半关系，因此，可以做∠A的平分线，利用等腰三角形三线合一的性质，把?∠A放在直角三角形中求解；也可以把∠DBC沿BD翻折构造2∠DBC求解。

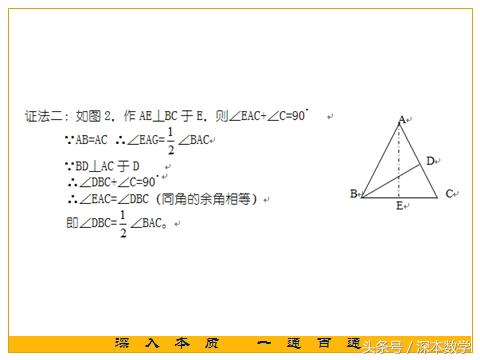
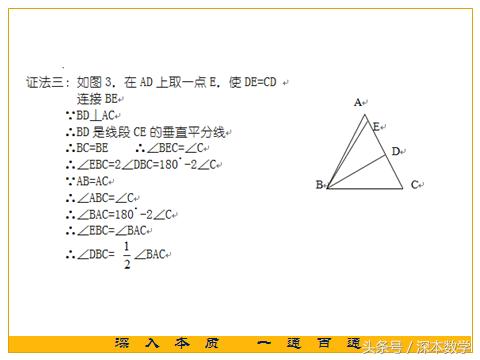
其实在上面的例题中，也可以取BC中点为E，连接DE，利用直角三角形斜边的中线等于斜边的一半和等腰三角形的性质求解。感兴趣的同学们不妨试一试，这道题目还有别的解法，同学们只有深入本质，弄通情景，不断地思考，才能在遇到题目的时候，举一反三。

欢迎大家在评论处留言讨论！