《2017年中考攻略》方程(组)应用探讨

一个可以真正学习的平台!
初中数学中列方程(组)解应用题是一项重要内容,也是中考中与不等式(组)的应用二选一(或同题)的必考内容。初中阶段主要包括一元一次、二次方程,分式方程,二元一次方程组(有些地区还有无理方程和可化为二元一次方程的高次方程组)。它们应用的基本步骤是相同的,基本步骤为:
①审(审题);
②找(找出题中的已知量、未知量和所涉及的基本数量关系、相等关系);
③设(设定未知数,包括直接未知数或间接未知数);
④表(用所设的未知数的代数式表示其他的相关量);
⑤列(列方程(组));
⑥解(解方程(组));
⑦验(检验解的有效性和实际意义的符合性);
⑧答(回答题问)。
它们的应用包括(1)行程问题;(2)工程问题;(3)溶度问题;(4)增长率问题;(5)销售利润和存贷问题;(6)比例和调配(分配)问题;(7)数字问题;(8)和差倍分问题;(9)几何问题;(10)分段问题;(11)规律探究问题;(12)不定方程问题;(13)在函数问题中的应用问题。下面通过近年全国各地中考的实例探讨其应用。
一、行程问题
解题指导:
(1)基本量是:路程、速度和时间。
基本关系是:①路程= 速度×时间;②时间=路程/速度;③速度=路程/时间。
(2)基本类型:相遇问题;相背问题;追及问题;行船(风速)问题;环形跑道问题等。
(3)解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系,一般情况下问题就能迎刃而解。并且还常常借助画草图来分析,理解行程问题。
在不同的问题中,相等关系是灵活多变的。如相遇问题中多以路程作相等关系,而对有先后顺序的问题却通常以时间作相等关系,在行船(风速)问题中很多时候还用速度作相等关系。
行船(风速)问题是行程问题中的一种特殊情况,其速度在不同的条件下会发生变化:
①顺水(风)速度=静水(无风)速度+水流速度(风速);
②逆水(风)速度=静水(无风)速度-水流速度(风速)。
由此可得到行船(风速)问题中一个重要等量关系:
顺水(风)速度-水流速度(风速)=逆水(风)速度+水流速度(风速)=静水(无风)速度。

二、工程问题
解题指导:
(1)基本量是:工作量、工作效率、工作时间。
基本关系是:①工作量=工作效率×工作时间;②工作时间=工作量/工作效率;③工作效率=工作量/工作时间。
(2)基本类型:有工作总量和无工作总量。
(3)在工程问题中,若工作总量给出了明确的数量,此时工作效率也即工作速度;若没有给出明确的数量,一般常将全部工作量看作整体1,如果完成全部工作的时间为t,则工作效率为1/t。常见的相等关系有两种:①如果以工作量作相等关系,部分工作量之和=总工作量;②如果以时间作相等关系,完成同一工作的时间差=多用的时间。

三、溶度问题
解题指导:
(1)基本量是:溶质(纯净物)、溶剂(杂质)、溶液(混合物)、浓度(含量)。
基本关系是:①溶液=溶质+溶剂(混合物=纯净物+杂质);
②浓度=溶质/溶液×100%=溶质/(溶质+溶剂)×100%
纯度(含量)=纯净物/混合物×100%=纯净物/(纯净物+杂质)×100%;
③溶质=浓度×溶液=浓度×(溶质+溶剂)
(2)在溶液问题中关键量是“溶质”:“溶质不变”,混合前溶质总量等于混合后的溶质量,是很多方程应用题中的主要等量关系。
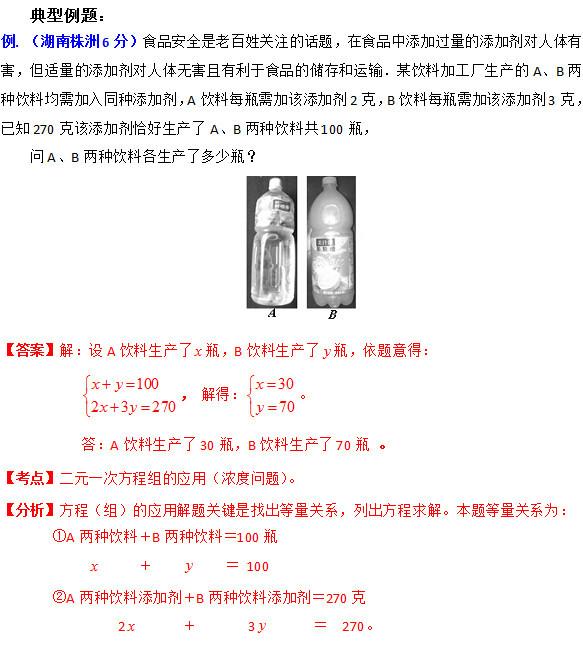
四、增长率问题
解题指导:
(1)基本量是:期初数、期末数、增长率。
基本关系:期末数=期初数×(1+增长率)。
(2)基本类型: 非连续增长和连续增长。
(3)在增长率问题中关键量是“增长率”。对于连续增长,增长率是相同的(平均增长率),连续两次增长后,期末数=期初数×(1+平均增长率)2。增长率问题还包括负增长,如降价。

题目太多今天就先介绍到这里,其他的后面在发,如果对你有帮助可以点击关注以免错过。
愿我的分享能够帮助到你!
相关文章
- 初二 | 如何破解含有参数的分式方程?
- 初中教育:中考重点题型,最短路径问题
- 中考方程式要牢记!
- 一元一次方程含参数问题的解题策略
- 【光学】折射问题怎么做?4类题型轻松解!
- 中考一元二次方程考点典型例题解析
- 秒杀一元二次函数值域问题
- 解一元一次方程计算题每天训练(15分钟)
- 都说预习很重要,怎样预习才最有效呢?
- 关于中考作文写作技巧的问题
- 中考一元二次方程应用题复习专题
- 一元二次方程总共有12个考点
- 孩子的“函数问题”还没有弄明白?掌握这些小技巧中考轻松涨10
- 【老师课件】一元一次方程应用题的10种类型,你掌握了吗?
- 20年教龄名师:初三学生的9大问题,越早知道越好!很中肯!
- 【中考】“一元二次方程解应用题”题型总结,转给需要的同学吧
- 几何最值问题,应该如何解决
- 破解中考之坐标几何题——坐标平面中的函数问题
- 初中以后,孩子成绩家长最关心的10个问题,一线名师为您解答
- 初一 | 一元一次方程应用题的等量关系,这篇文章都给你总结好了
推荐内容
教育新鲜事
 上课老走神怎么办?9张
上课老走神怎么办?9张 中考过来人传授经验
中考过来人传授经验 谁把初中各科答题套路编
谁把初中各科答题套路编 衡水中学关于考试的51条
衡水中学关于考试的51条