几何综合题主要分为直线型和与圆有关的几何综合题。

直线型的综合题主要包含三角形、四边形和相似三角形的知识。

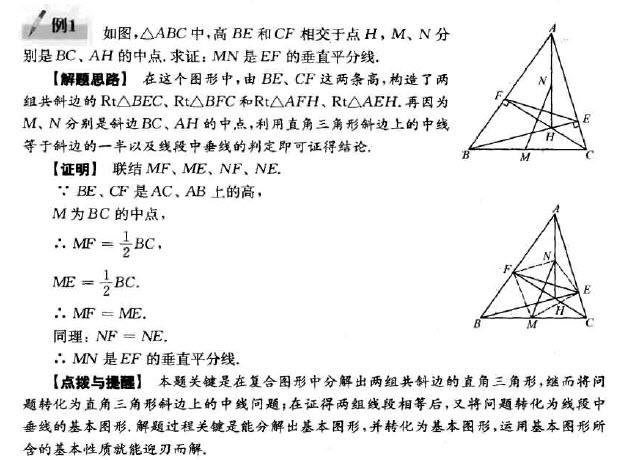
三角形和四边形主要是关于相等问题。证明线段、角相等的方法主要是证明全等三角形，即利用全等三角形的判定和性质。

其他方法还有：

运用等腰三角形的判定与性质'三线合一”性质；运用直角三角形的判定与性质；运用平行四边形的判定与性质；运用矩形、菱形、正方形的判定和性质；运用梯形、等腰梯形的判定和性质；运用梯形中位线、三角形中位线的性质；运用角的平分线上的点的性质与判定；运用线段垂直平分线上的点的判定与性质等等。

相似三角形主要是关于两个三角形中对应线段、周长、面积的比的问题.求两个三角形 的对应线段、周长的比可以运用相似三角形的性质和判定。

利用相似三角形的性质还可以证明比例线段。

与圆有关的几何综合题主要是包含圆与直线图形。

圆这部分内容有圆的基本性质。点圆、线圆.圆圆之间的位置关系：相切问题，圆与三角形的切割关系.特别是切线的判定与性质等等。

在几何综合题的解题过程中，有时需要添加辅助线.添加辅助线的原则是：一、运用基本图形的性质，补全基本图形，以利证明;二、运用图形运动的思想，将图形中分散的条件相对集中，产生新的图形，运用基本图形的性质证明。

在几何综合题的解题方法上，应将复合图形中的基本图形分解出来，将几个基本图形串连起来，利用基本图形的性质进行推理，建立一些相关联的等式，可以利用方程、三角等 方法解决。

在几何综合题的解题过程中，通常要用到分类讨论、化归、函数、方程、图形运动和图形的分解与组合等数学思想方法，运用这些数学思想方法.将未知问题转化为已知问题，一步 一步解决各个问题，最终达到完整的结论.。

一、直线型几何综合