一篇文章,掌握函数图像,不看别后悔!
函数的图像是高考的必考点,对于研究函数的单调性、奇偶性以及最值(值域)、零点有举足轻重的作用,但是很多同学看到眼花缭乱的函数解析式,就已经晕头转向了,再去画图像,不是这里错,就是那里有问题,图像也画的乱七八糟,更甭提利用图像去解题了!
其实,小数老师看来,画函数图像有以下几步:
首先,观察是否是基本初等函数(也就是我们在课本中学过的那几类函数),如果是,那就可以画了;
如果不是,继续第二步,看看是否是经过一系列函数变换的,比如:翻折变换,对称变换,伸缩变换,平移变换等,如果是,那就根据变换的规律画出图像,如果还不是,那基本这个函数图像也不需要你独自画出来了,那种题目基本会考察选择题,能从4个选项中选择出来就可以了!(今天不研究那种函数图像)
下面,小数老师给大家整理一下基本初等函数的图像以及函数变换的规律,希望大家能学明白!
一、基本初等函数的图像
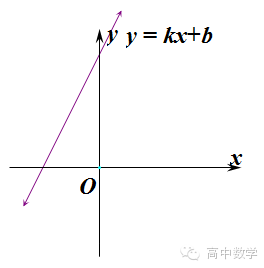
性质:一次函数图像是直线,当k>0时,函数单调递增;当k<>时,函数单调递减
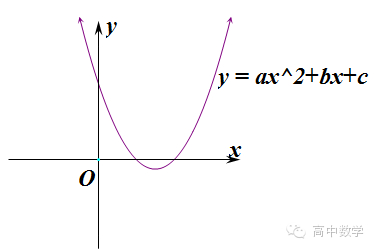
性质:二次函数图像是抛物线,a决定函数图像的开口方向,判别式b^2-4ac决定了函数图像与x轴的交点,对称轴两边函数的单调性不同。
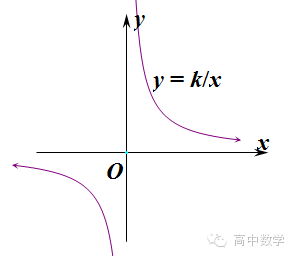
性质:反比例函数图像是双曲线,当k>0时,图像经过一、三象限;当k<>时,图像经过二、四象限。要注意表述函数单调性时,不能说在定义域上单调,而应该说在(-∞,0),(0,∞)上单调。
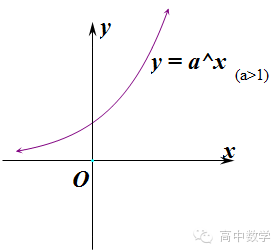
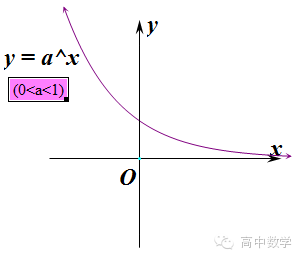
当0<><><><><>时,指数函数的图像如下图
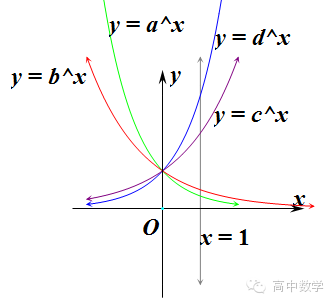
不同底的指数函数图像在同一个坐标系中时,一般可以做直线x=1,与各函数的交点,根据交点纵坐标的大小,即可比较底数的大小。
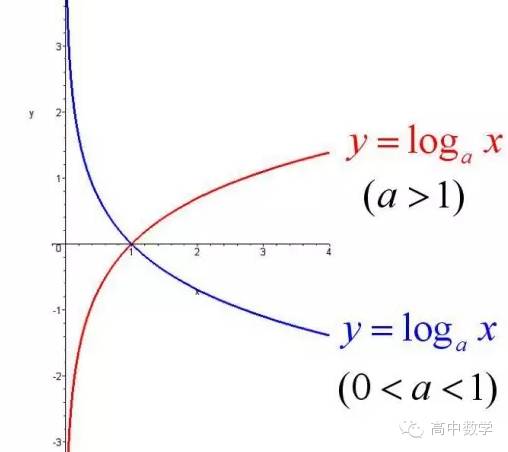
当底数不同时,对数函数的图像是这样变换的
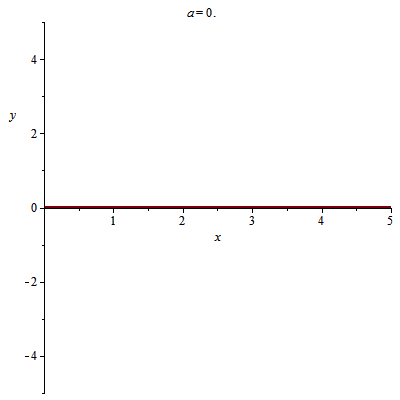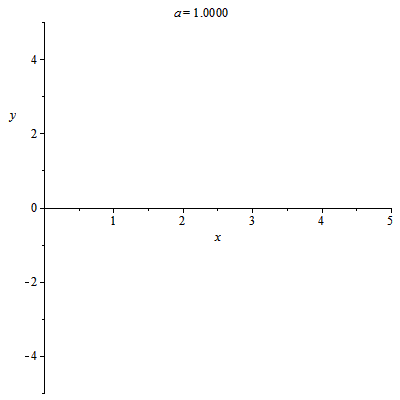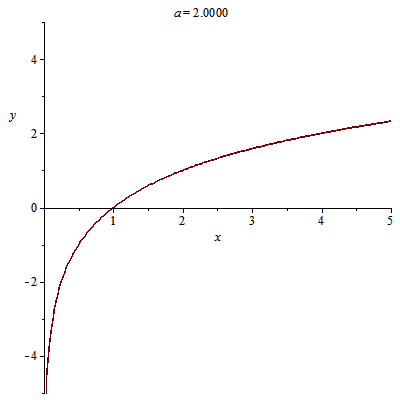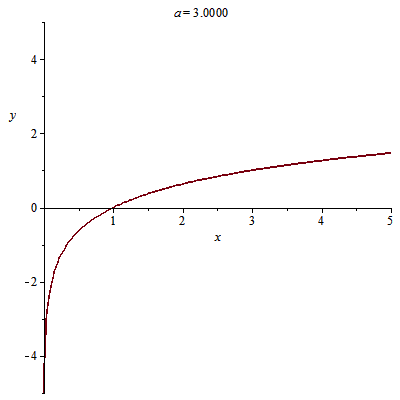
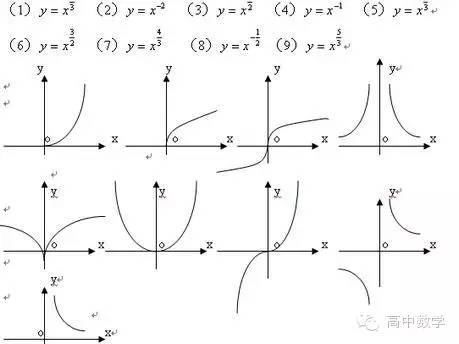
性质:
先看第一象限,即x>0时,当a>1时,函数越增越快;当0<><>时,函数越增越慢;当a<>时,函数单调递减;然后当x<>时,根据函数的定义域与奇偶性判断函数图像即可。
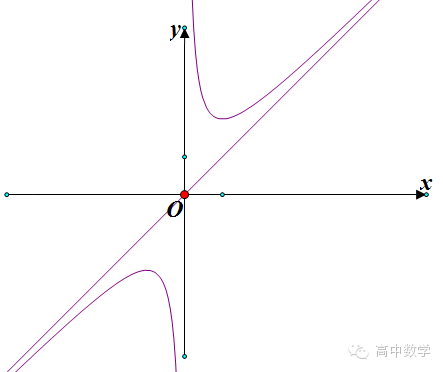
对于函数y=x+k/x,当k>0时,才是对勾函数,可以利用均值定理找到函数的最值。
二、函数图像的变换

注意:对于函数图像的变换,有的时候,看到解析式,可能会有两种以上的变换,尤其是针对x轴上的,那么此时,一定要根据上面的规则,判断好顺序,否则顺序错了,可能就没办法经过变换得到了!
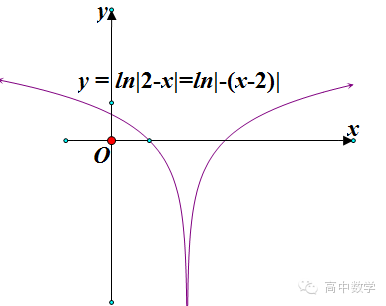
例如:画出函数y=ln|2-x|的图像
通过研究这个函数解析式,我们知道此函数是由基本初等函数y=lnx通过变换而来,那么这个函数经过了几步变换呢?变换的顺序又是如何?下面我们一起来看一看
通过解析式x上附加的东西,我们会发现,会有对称变换,x前面加了负号,还有翻折变换,x上面还有绝对值,还有平移变换,前面加了一个2,既然有3种变换,那么顺序如何呢?牢记住一点:针对x轴上的变换,那就一定要看x这个符号有啥变化。
所以,我们可以得出:第一步,翻折变换;第二步,对称变换;第三步,平移变换。
有的同学说,第一步是对称变换,也就是先在x上加负号,但是接下来的话,再进行翻折变换,就相当于在-x上加绝对值了,而这个并不是我们学过的规律,所以后面就无法进行变换了,这样也就错了。同学们一定要切记哈!
当然,如果同学们能对这四种变换很熟悉的话,那就可以先对解析式进行变形,化为y=ln|x-2|,这样只经过两步变换即可了!下面是这个函数的图像,
第一步:先画出函数y=lnx的图像
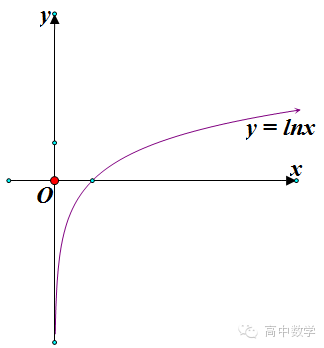
第二步:进行翻折变换,得到函数y=ln|x|的图像
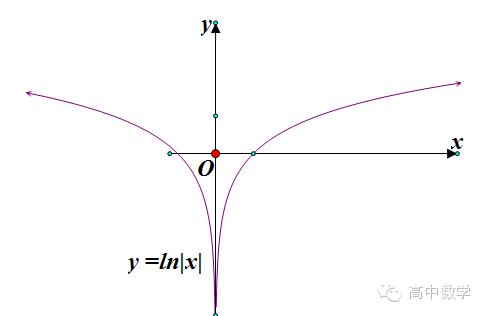
第三步:进行对称变换,得到函数y=ln|-x|的图像
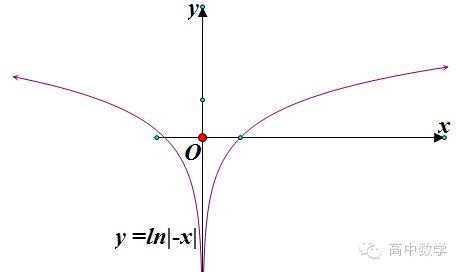
第四步:进行对称变换,得到函数y=ln|2-x|的图像
相关文章
- 三角函数就考这6个题型,你掌握了吗?
- “三角函数”的题型只有这6种,最完整的解析过程,老师点头称赞
- 一人一句高考各科易错点汇总,帮你速提50分!
- 构造+单调+根判定结合的非常完美!
- 定位快速突破分段函数求值问题
- 抓七点快速突破函数图像问题
- 两角和与差的三角函数
- 高考热点:函数与方程思想、数形结合思想
- 20、高中理科入门20 函数单调性判断2 复合函数单调性
- 那些高中老师不会讲,但解题时非常好用的知识
- 高考要考的函数图像与性质,全了!
- 20、高中理科入门20 函数单调性判断1
- 18、高中理科入门18 求函数解析式
- 函数的周期性
- 20、高中理科入门 奇偶性性函数的函数值和函数解析式
- 19、高中理科入门19 函数的周期
- 20、高中理科入门20 函数奇偶性1
- 16、高中理科入门16 函数的值域
- 高中函数做了千万遍?不如记住这几个口诀
- 求函数解析式的基本方法(1)
推荐内容
教育新鲜事
 高中丨(高频考点)物理
高中丨(高频考点)物理 期末考试时间定了!收官
期末考试时间定了!收官 高中生逆袭物语:这几步
高中生逆袭物语:这几步 必须收藏!省略句考点全
必须收藏!省略句考点全