椭圆的四类最值问题
一、的最值
若A为椭圆内一定点(异于焦点),P是C上的一个动点,F是C的一个焦点,e是C的离心率,求的最小值。
例1、已知椭圆内有一点A(2,1),F是椭圆C的左焦点,P为椭圆C上的动点,求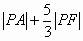 的最小值。
的最小值。
分析:注意到式中的数值“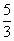 ”恰为
”恰为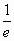 ,则可由椭圆的第二定义知
,则可由椭圆的第二定义知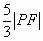 等于椭圆上的点P到左准线的距离。答案为
等于椭圆上的点P到左准线的距离。答案为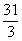 。
。
二、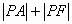 的最值
的最值
若A为椭圆C内一定点(异于焦点),P为C上的一个动点,F是C的一个焦点,求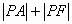 的最值。
的最值。
例2、已知椭圆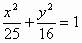 内有一点A(2,1),F为椭圆的左焦点,P是椭圆上动点,求
内有一点A(2,1),F为椭圆的左焦点,P是椭圆上动点,求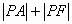 的最大值与最小值。
的最大值与最小值。
解:如图1,设椭圆的右焦点为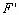 ,可知其坐标为(3,0)
,可知其坐标为(3,0)
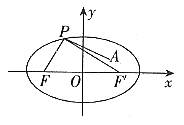
图1
由椭圆的第一定义得: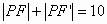
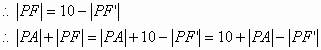
可知,当P为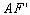 的延长线与椭圆的交点时,
的延长线与椭圆的交点时,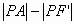 最大,最大值为
最大,最大值为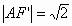 ,当P为
,当P为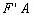 的延长线与椭圆的交点时,
的延长线与椭圆的交点时,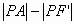 最小,最小值为
最小,最小值为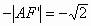 。
。
故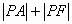 的最大值为
的最大值为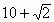 ,最小值为
,最小值为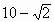 。
。
三、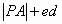 的最值
的最值
若A为椭圆C外一定点,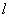 为C的一条准线,P为C上的一个动点,P到
为C的一条准线,P为C上的一个动点,P到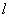 的距离为d,求
的距离为d,求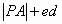 的最小值。
的最小值。
例3、已知椭圆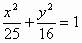 外一点A(5,6),
外一点A(5,6),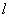 为椭圆的左准线,P为椭圆上动点,点P到
为椭圆的左准线,P为椭圆上动点,点P到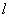 的距离为d,求
的距离为d,求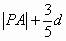 的最小值。
的最小值。
解:如图2,设F为椭圆的左焦点,可知其坐标为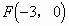
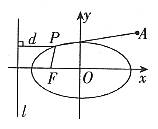
图2
根据椭圆的第二定义有: ,即
,即
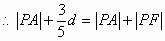
可知当P、F、A三点共线且P在线段AF上时,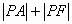 最小,最小值
最小,最小值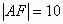 。
。
故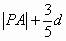 的最小值为10。
的最小值为10。
四、椭圆上定长动弦中点到准线距离的最值
例4、定长为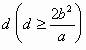 的线段AB的两个端点分别在椭圆
的线段AB的两个端点分别在椭圆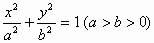 上移动,求AB的中点M到椭圆右准线
上移动,求AB的中点M到椭圆右准线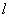 的最短距离。
的最短距离。
解:设F为椭圆的右焦点,如图3,作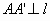 于A”,BB”⊥
于A”,BB”⊥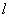 于B”,MM”⊥
于B”,MM”⊥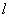 于M”
于M”
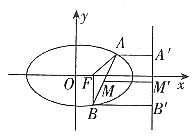
图3
则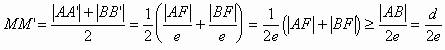
当且仅当AB过焦点F时等号成立。
故M到椭圆右准线的最短距离为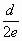 。
。
注: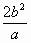 是椭圆的通径长,是椭圆焦点弦长的最小值,
是椭圆的通径长,是椭圆焦点弦长的最小值, 是AB能过焦点的充要条件。
是AB能过焦点的充要条件。
推荐内容
教育新鲜事




 高中丨(高频考点)物理
高中丨(高频考点)物理 期末考试时间定了!收官
期末考试时间定了!收官 高中生逆袭物语:这几步
高中生逆袭物语:这几步 必须收藏!省略句考点全
必须收藏!省略句考点全