数学破题36计第32计 立几开门 平面来风
第32计 立几开门 平面来风?
●计名释义?
空间型试题感到困难怎么办?退到平面去,平面是立体几何的基础,“空间几何平面化”是我们的基本手段.“平面化”的主要形式有:(1)展开图,把空间展到平面;(2)三视图,从不同的角度看平面;(3)射影图,把一个平面放到另一个平面去;(4)截面图,把我们关心的平面进行特写.如此等等,可以把直观图中的错觉或误差分别转移到平面上作“真实分析”.??
●典例示范?
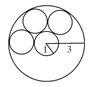 【例1】 “神舟六号”飞船上
【例1】 “神舟六号”飞船上
使用一种非常精密的滚球轴承,
如图所示,该滚球轴承的内
外圆的半径分别为1mm、3mm?,
则这个轴承里最多可放
滚珠 个. 例1题图?
【解答】 6如图,设两滚球P,Q相切
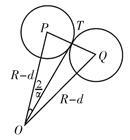 于点T,轴承中心为O,连接OT,
于点T,轴承中心为O,连接OT,
设滚球半径为d,内、外圆半径
分别为r、R,则R=3,d=r=1.?
在Rt△OTP中,∠POT=![]() ,OP=2,PT=1,?
,OP=2,PT=1,?
则有sin![]() =
=![]() ,
,
得α=2×![]() =
=![]() ,即在圆心角为
,即在圆心角为![]() 的轨道内,
例1题解图
的轨道内,
例1题解图
可放一个滚珠,故圆心角为周角(2π弧度)
时可放的滚珠为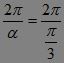 =6个.?
=6个.?
【点评】 本题考查了球体知识的相切问题,把复杂的空间立体图形简化成平面图形来解决.??
【例2】
在正四棱柱ABCD—A1B1C1D1中,底面四边形ABCD边长为3,高为4,在棱C1B1,C1D,CC?上分别取一点M、N、L使C1M=C1N=1,C1L=![]() .?
.?
(1)求证:对角线AC1⊥面MNL;? (2)求四面体D—MNL的体积;?
(3)求AM和平面MNL所成夹角的正弦值.?
【思考】 (1)本题并不难,但其手法还是“退”,由证线面垂直退到证线线垂直.根据对称性,只需证AC1与LM、LN之一垂直即可;?
(2)四面体D—MNL的体积不好求,可退而求四面体C1—MNL的体积,这两个四面体等底不等高,再退而求四面体对应高之比,然后将所求四面体C1—MNL的体积适当扩大即可;?
(3)AM与面MAC1夹角的正弦不好求,可退而求AM、AC1夹角的余弦.?
【解答】 (1)如图所示,以D1为原点,直线D1A1,D1C1,D1D分别为x,y,z轴建立空间坐标系,?
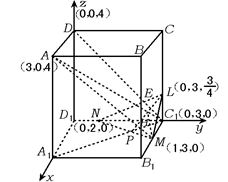 则有:A(3,0,4),C?1(0,3,0)?
则有:A(3,0,4),C?1(0,3,0)?
∴![]() =(-3,3,-4);L
=(-3,3,-4);L![]() ,N(0,2,0),?
,N(0,2,0),?
∴![]() =
=![]() ∵
∵![]() ·
·![]() =0+3-3=0,?
=0+3-3=0,?
∴![]() ⊥
⊥![]() ,根据图形对称性,
,根据图形对称性,
同理有![]() ⊥
⊥![]() ,故AC1⊥平面MNL.? 例2题解图
,故AC1⊥平面MNL.? 例2题解图
(2)四面体D—MNL与C1—MNL同底不等高,设其高分别为h1,h2,连C1D交NL于E.?
∵D(0,0,4),?
∴![]() =(0,-3,4),且
=(0,-3,4),且![]() ·
·![]() =(0,-3,4)·
=(0,-3,4)·![]() =0.?
=0.?
∴![]() ⊥
⊥![]() ,知L、E、D、C在同一个圆上,|
,知L、E、D、C在同一个圆上,|![]() |·?|
|·?|![]() |?=|
|?=|![]() |·|
|·|![]() |,
|,
即![]() ·4=|
·4=|![]() |·5.
|·5.
∴|![]() |=
|=![]() ,从而|
,从而|![]() |=5-
|=5-![]() =
=![]() .?
.?
h1∶h2=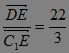 .?
.?
易求VC?1-MNL=![]() ·C1M·C1N·C1L=
·C1M·C1N·C1L=![]() ×1×1×
×1×1×![]() ,∴VD-MNL?=
,∴VD-MNL?=![]() =
=![]() (立方单位).?
(立方单位).?
(3)设AM与平面AC1成θ角,已证AC1⊥平面MNL,∴∠MAC1=90°-θ.?
∵M(1,3,0),∴![]() =(-2,3,-4),
=(-2,3,-4), ![]() ·
·![]() =(-2,3,-4)·(-3,3,-4)=6+9+16=31.?
=(-2,3,-4)·(-3,3,-4)=6+9+16=31.?
又|![]() |=
|=![]() ,
,
|![]() |=
|= ![]() .?
.?
∴cos (90°-θ)=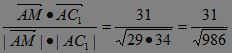 .?从而?sin?θ=
.?从而?sin?θ=![]() ,即AM与平面MNL所成角的正弦值为
,即AM与平面MNL所成角的正弦值为![]() .?
.?
【评注】 本题第(2)问另一解法:∵VD-MNL?=VM-DNL,而S△DNL?易求,且MC1⊥面DNL,从而VD-MNL =![]() ·S△DNL?·MC1也不失为另一有效解法.??
·S△DNL?·MC1也不失为另一有效解法.??
【例3】 (04·全国卷Ⅲ)如图,
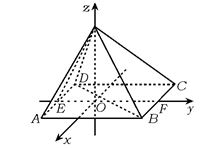 四棱锥P—ABCD中,底面ABCD为矩形,
四棱锥P—ABCD中,底面ABCD为矩形,
AB=8,AD=4![]() ,侧面PAD为等边
,侧面PAD为等边
三角形,并且与底面所成二面角为60°.?
(Ⅰ)求四棱锥P—ABCD的体积;?
(Ⅱ)求证:PA⊥BD.?
【分析】 1.题目没有讲是“正”四棱锥,
不要粗心地乱加条件“按正棱锥”解题,
否则是“瞎子点灯”——白费蜡,
因此,顶点在底面的射影不一定是底面的中心.? 例3题图
2.图中的三角因素很多,证垂直的最好办法是利用向量.因而制定三角加向量的解题策略.?
【解答】 (Ⅰ)设O为P在底面的射影,作OE⊥AD于E,连PE,则∠PEO是二面角P—AD—O的平面角,有∠PEO=60°.已知△PAD为正三角形,且边长为4![]() .
.
∴|PE|=4![]() sin60°=6,PO=6sin60°=3
sin60°=6,PO=6sin60°=3![]() .?
.?
∴VP—ABCD=![]() ·S□ABCD?·PO=
·S□ABCD?·PO=![]() ·8·4
·8·4![]() ·3
·3![]() ]=96(立方单位).?
]=96(立方单位).?
(Ⅱ)以O为原点,平行于AD的直线为x轴,平行于AB的直线为y轴,垂线OP所在直线为z轴建立如图的空间直角坐标系.?
则有P(0,0,3![]() ),A(2
),A(2![]() ,-3,0),B(2
,-3,0),B(2![]() ,5,0),D(-2
,5,0),D(-2![]() ,-3,0),?
,-3,0),?
∴![]() =(2
=(2![]() ,-3,-3
,-3,-3![]() ),?
),?![]() =(-4
=(-4![]() ,-8,0),?
,-8,0),?
∵![]() ·
·![]() =-24+24+0=0.?
∴
=-24+24+0=0.?
∴![]() ⊥
⊥![]() .??
.??
●对应训练?
1.如图所示,ABCD是边长
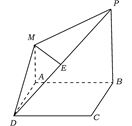 为2a的正方形,
为2a的正方形,
PB⊥平面ABCD,
MA∥PB,且PB=2MA=2a,
E是PD的中点??
(1)求证:ME∥平面ABCD;?
(2)求点B到平面PMD的距离;?
(3)求平面PMD与平面
ABCD所成二面角的余弦值??? 第1题图
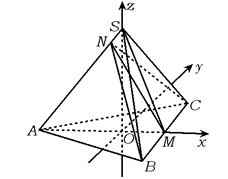
2.在正三棱锥S—ABC中,底面是边长为a的正三角形,点O为△ABC的中心,点M为边BC的中点,AM=2SO,点N在棱SA上,且SA=25SN.?
(Ⅰ)求面SBC与底面ABC所成二面角的大小;?
(Ⅱ)证明:SA⊥平面NBC.?
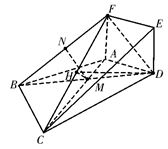
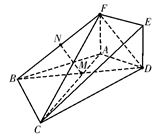 3.如图,边长为2的正方形ADEF所在的
3.如图,边长为2的正方形ADEF所在的
平面垂直于平面ABCD,AB=AD,
AB⊥AD,AC=3![]() ,AC⊥BD,
,AC⊥BD,
垂足为M,N为BF的中点.?
(1)求证:MN∥平面ADEF;?
(2)求异面直线BD与CF所成角的大小;?
(3)求二面角A-CF-D的大小.? 第3题图
●参考答案?
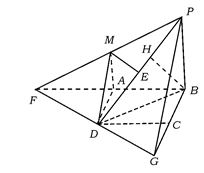
1.(1)延长PM、BA交于F,连接FD,FD、BC延长交于G,连接PG,?
∵MA![]()
![]() PB=a,?
PB=a,?
 ∴M为PF中点,又E为PD中点,?
∴M为PF中点,又E为PD中点,?
∴ME为△PFD中位线,ME∥FD,
而FD平面ABCD,?
∴ME∥平面ABCD.?
(2)MA?/span>![]()
![]() PB时,A为FB的中点.?
PB时,A为FB的中点.?
∵四边形ABCD是正方形,∴AD∥BC,DC∥AB,
∴D、C分别为FG、BG的中点. 第1题解图
∵AB=BC=2a. ∴BF=BG=4a. ∴BD⊥FG,∵PB⊥平面ABCD,∴PB⊥FG,故FG⊥平面PBD. 作BH⊥PD于H,必FG⊥BH,
故BH⊥平面PFG,BH之长是点B到平面PFG(也就是平面PMD)的距离.?
?Rt△PBD中,PB=2a,BD=2![]() a.?
a.?
∴PD=![]() =2
=2![]() a,BH=
a,BH=![]() a,即所求距离为
a,即所求距离为![]() a.?
a.?
(3)由(2)知FG⊥DB,FG⊥DP. ∴∠PDB是二面角P-FG-B的平面角,且
cos∠PDB=![]() ,即所求二面角的余弦值为
,即所求二面角的余弦值为![]() .?
.?
点评: (1)解立体几何题有两句格言:一是空间问题平面化,一是不规则图形规则化.本解中“规则化”的手段是补形,最终补成底面为等腰直角三角形且高与底面垂直的规则四面体,以下的分析计算也就方便了.?
(2)将正方体截下一个角,所得四面体由于有三条侧棱两两垂直,我们称这样的四面体为直角四面体,直角四面体有许多重要性质,其中最重要的有3条:?
①若用S,S1,S2,S3分别表示直角四面体的底面积和三个侧面积,那么:S2=S 21+S 22+S 23?
②若直角四面体的三条侧棱之长依次为a,b,c,则其底面积:S=![]()
![]()
③若直角四面体的三条侧棱之长,依次为a,b,c,且直角顶点到底面的距离为h,那么?
h=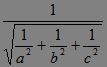 .?
.?
根据公式③本题第2问可轻而易举地解决:图中B—PFG为直角四面体,且BP=2a,BF=BG=4a?
∴BH=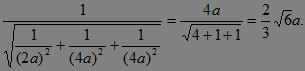 ?
?
2.(1)如图,正△ABC边长为a时,
 AM=
AM=![]() a,OM=
a,OM=![]() AM=
AM=![]() a.
a.
SO=![]() AM=
AM=![]() a.?
a.?
∠SMA是二面角S—BC—A的平面角,
设为α,则tanα=![]() .
.
∴面SBC与面ABC成arctan![]() 的角.?
第2题解图
的角.?
第2题解图
(2)以O为原点,直线AM、OS分别为x,z轴,过O且平行于BC的直线为y轴建立如图的空间直角坐标系,则有B(![]() a,
a,![]() ,0),M(
,0),M(![]() a,0,0),C (
a,0,0),C (![]() a,
a,![]() ,0),S (0,0,
,0),S (0,0, ![]() a).?
a).?
∵![]() a,有A(-
a,有A(-![]() a,0,0).?
a,0,0).?
∵![]() =(-
=(-![]() a,0,-
a,0,-![]() a),
a),![]() =(0,a,0),
∴?
=(0,a,0),
∴?![]() ·
·![]() =0,?
=0,?![]() ⊥
⊥![]() .?
.?
又![]() =
=![]()
![]() ,故有N(
,故有N(![]() a,0,
a,0,![]() a).
a). ![]() =
=![]() a,0,-
a,0,-![]() a).?
a).?
故![]() ·
·![]() =(-
=(-![]() a,0,-
a,0,- ![]() a)·(
a)·(![]() a,0,-
a,0,-![]() a)= -
a)= -![]() a2 +0+
a2 +0+![]() a2 =0.?
a2 =0.?
∴![]() ?⊥
?⊥![]() ,从而SA⊥平面NBC.?
,从而SA⊥平面NBC.?
3.方法一:(1)∵AB=AD,AC⊥BD,垂足为M,∴M为BD的中点,∵N为BF中点,∴MN∥DF?
∵MN面ADEF,DF面ADEF,∴MN∥平面ADEF.?
(2)∵平面ADEF⊥平面ABCD,又∵FA⊥AD,∴FA⊥面ABCD,?
∵AC是FC在平面ABCD内的射影,BD⊥AC,∴BD⊥CF,?
∴异面直线BD与CF所成角的大小为90°.?
(3)在平面ACF内过M作MH⊥CF于H,连DH,?
∵BD⊥AC,BD⊥CF,AC∩CF=C,?
∴BD⊥面ACF,斜线DH在平面ACF内的射影是MH,?
又CF⊥MH,∴CF⊥DH,∴∠MHD是二面角A-CF-D的平面角.?
在等腰Rt△ABD中,DM=![]() ,AM=
,AM=![]() ,∵AC=3
,∵AC=3![]() ,∴CM=2
,∴CM=2![]() ,CF=
,CF=![]() ,?
,?
∵△CMH∽△CFA,∴![]() ,∴MH=
,∴MH=![]() ,?tanMHD =
,?tanMHD =![]() ,?
,?
∴二面角A-CF-D的大小为?arctan![]() .?
.?
方法二:(1)同法一;?
(2)∵平面ADEF⊥平面ABCD,又∵FA⊥AD,∴FA⊥面ABCD,?
∴平面FAC⊥平面ABCD,在平面FAC内作MG⊥AC交FC于点G,?
∴MG⊥平面ABCD.?
如图,建立空间直角坐标系M-xyz,?
则C(2![]() ,0,0),B(0,-
,0,0),B(0,-![]() ,0),D(0,
,0),D(0,![]() ,0),F(-
,0),F(-![]() ,0,2),?
,0,2),?
∴![]() =(0,2
=(0,2![]() ,0),
,0),![]() =(3
=(3![]() ,0,-2),∴
,0,-2),∴![]() ·
·![]() =0,∴
=0,∴![]() ?⊥
?⊥![]() .?
.?
∴异面直线BD与CF所成角的大小为90°.?
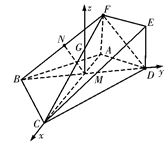

第3题解图(1) 第3题解图(2) 第3题解图(3)
(3)设n=(x,y,z)是平面CFD的法向量,?
∵![]() =(3
=(3![]() ,0,-2),
,0,-2),![]() =(
=(![]() ,
,![]() ,-2),?
,-2),?
由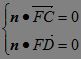 ,∴
,∴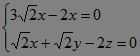 ,令z=3,则x=
,令z=3,则x=![]() ,y=2
,y=2![]() ,?
,?
∴n=(![]() ,2
,2![]() ,3),∵MD⊥AC,∴MD⊥平面ACF?
,3),∵MD⊥AC,∴MD⊥平面ACF?
∴平面ACF的法向量![]() =(0,
=(0,![]() ,0),则cos<n,
,0),则cos<n,![]() >=
>=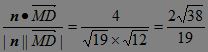 .?
.?
∴二面角A-CF-D的大小为arccos![]() .??
.??
相关文章
- 高中数学多样解题,一题突破平面向量所有难点!
- 2017高考数学 点、直线、平面之间的位置关系
- 高考数学兵法10招(2)就地取材,无中生有
- 高考金钥匙数学解题技巧大揭秘专题十三 空间线面位置关系的推理
- 2017高考数学 平面向量四心向量表示大突破
- 高中数学平面向量知识点总结
- 高考金钥匙数学解题技巧大揭秘专题十四 用空间向量法解决立体几
- 高考数学难点突破28求空间距离
- 高考数学难点突破27求空间的角
- 数学破题36计第14计 鲜花开门 情有独钟
- 高中数学典型例题解析(第七章平面解析几何初步2)
- 2017高考数学平面向量的应用
- 2017高考数学平面向量的数量积
- 高一数学《空间点、直线、平面的位置关系》知识点总结
推荐内容
教育新鲜事
 高中数学“函数”必考知
高中数学“函数”必考知 高考数学答题方法的19条
高考数学答题方法的19条 高考数学干货丨最容易出
高考数学干货丨最容易出 【高中数学】《三角函数
【高中数学】《三角函数