埃伦费斯特和他的浸渐原理
如果说,玻尔的对应原理是在经典物理学和量子力学之间架起的一座桥梁,那么,埃伦费斯特(PaulEhrenfest,1880—1933)的浸渐原理则是两者之间的又一座桥梁。“浸渐(Adiabatic)”表示无限缓慢的变化过程,也可译“绝热”,但意义不够准确。这个概念起源于玻尔兹曼和克劳修斯企图将热力学第二定律还原为纯力学的尝试。玻尔兹曼在1866年证明,假如制约力学体系行为的定律服从最小作用原理,则周期为τ的简单周期性体系的动能为:

为此,曾于1912年专程走访爱因斯坦。爱因斯坦对他的思想给予很高评价,1914年称埃伦费斯特的原理为“浸渐假说”。埃伦费斯特是奥地利人,生于1880年,在维也纳大学听过玻尔兹曼讲授热的分子运动论。1904年获博士学位后从事统计物理学研究。鉴于他出色的理论素养,洛仑兹在1912年推荐他接任自己在荷兰莱顿大学的教授职务。此后,埃伦费斯特一直在莱顿大学主持工作。
1912年底,埃伦费斯特在与洛仑兹的通信中提出一个重要思想,他写道①:“一个被镜面器壁限制的体积,里面充满了辐射,正在作无限缓慢的压缩,对所有振动模式来说,有一个量E/v应保持常数,故可写为δ(E/ν)=0(内'为‘浸渐、可逆’变量)”,他问道:“假如从简谐振动变换到别的周期运动,什么量(可以代替E/ν)在‘浸渐可逆’过程中保持常数呢?”1913年,埃伦费斯特的论文经洛仑兹介绍发表在荷兰的阿姆斯特丹科学院学报上,题为《玻尔兹曼的力学理论及其与能量子理论的关系》,他提出一条原理:两相互以浸渐变换联系的体系A、B之间存在如下关系:
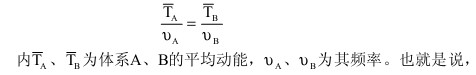
1918年,他给埃伦费斯特的信中写道:“您可以看到,这些内容(指玻尔当时发表的论文)在很大程度上是基于您的重要原理——浸渐不变性原理。不过根据我的理解,我是从多少有点不同的观点来考虑问题。因此我没有用您的原始论文所用的那些词汇。在我看来,定态之间运动的连续转变条件可以看成是保证这些状态稳定性的直接结果,其主要问题在于如何判断将普通‘力学’用于计算体系的连续转变效应的正确性。因为我似乎以为,不太可能把这一判断完全置于热力学的考虑,而很自然地应从用普通力学计算定态与实验的一致性上进行判断。”

为此,曾于1912年专程走访爱因斯坦。爱因斯坦对他的思想给予很高评价,1914年称埃伦费斯特的原理为“浸渐假说”。埃伦费斯特是奥地利人,生于1880年,在维也纳大学听过玻尔兹曼讲授热的分子运动论。1904年获博士学位后从事统计物理学研究。鉴于他出色的理论素养,洛仑兹在1912年推荐他接任自己在荷兰莱顿大学的教授职务。此后,埃伦费斯特一直在莱顿大学主持工作。
1912年底,埃伦费斯特在与洛仑兹的通信中提出一个重要思想,他写道①:“一个被镜面器壁限制的体积,里面充满了辐射,正在作无限缓慢的压缩,对所有振动模式来说,有一个量E/v应保持常数,故可写为δ(E/ν)=0(内'为‘浸渐、可逆’变量)”,他问道:“假如从简谐振动变换到别的周期运动,什么量(可以代替E/ν)在‘浸渐可逆’过程中保持常数呢?”1913年,埃伦费斯特的论文经洛仑兹介绍发表在荷兰的阿姆斯特丹科学院学报上,题为《玻尔兹曼的力学理论及其与能量子理论的关系》,他提出一条原理:两相互以浸渐变换联系的体系A、B之间存在如下关系:
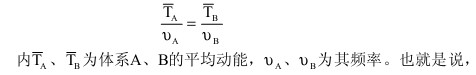
1918年,他给埃伦费斯特的信中写道:“您可以看到,这些内容(指玻尔当时发表的论文)在很大程度上是基于您的重要原理——浸渐不变性原理。不过根据我的理解,我是从多少有点不同的观点来考虑问题。因此我没有用您的原始论文所用的那些词汇。在我看来,定态之间运动的连续转变条件可以看成是保证这些状态稳定性的直接结果,其主要问题在于如何判断将普通‘力学’用于计算体系的连续转变效应的正确性。因为我似乎以为,不太可能把这一判断完全置于热力学的考虑,而很自然地应从用普通力学计算定态与实验的一致性上进行判断。”
相关文章
教育新鲜事
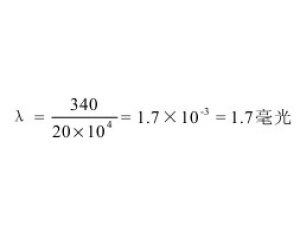 “超声“和“超音”
“超声“和“超音” 集市一瞥
集市一瞥 昆明湖上
昆明湖上 背道而驰
背道而驰