索末菲全面推广玻尔理论(2)
其中α是Pψ与极轴间的夹角。这一方程表示轨道平面与极轴之间的倾角存在分立性,这就是“空间量子化”。如果极轴有一确定方向,例如由于外磁场和外电场而确定了方向,则这个关系具有明确的物理意义。空间量子化是索末菲提出的一个重要概念,可以对斯塔克效应和塞曼效应提供相当满意的描述。后来,朗德(AlfredLandé)和斯梅卡尔(AdolfSmekal)甚至还用之于解释X射线谱,讨论氦光谱等等。及至1922年,斯特恩(OttoStern)和盖拉赫(WaltherGerlach)用他们的银原子束在不均匀磁场中证实了空间量子化的实际存在。
然而,空间量子化并不能解释氢光谱的精细结构。索末菲将相对论用于电子的周期运动,证明电子在有心力的作用下将作玫瑰花环形的运动,或者作近日点缓慢进动和以原子核为集点之一的椭圆运动。他用分离变量法求解哈密顿-雅可比微分方程,再用傅里叶级数展开,得到能量:
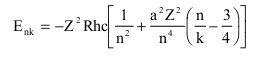
1920年他进一步对碱金属的谱线作出解释。索末菲开创的用相对论处理原子问题的方法后来又经过许多人的研究,继续有所进展,但仍然存在许多障碍,例如光谱强度问题、反常塞曼效应问题等等,看来根本的出路在于建立一套适合于微观体系的崭新理论,靠修补是无济于事的。在这里,要说明一个重要问题。不论是普朗克、威尔逊、石原纯还
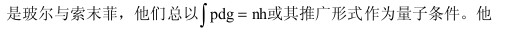
然而,空间量子化并不能解释氢光谱的精细结构。索末菲将相对论用于电子的周期运动,证明电子在有心力的作用下将作玫瑰花环形的运动,或者作近日点缓慢进动和以原子核为集点之一的椭圆运动。他用分离变量法求解哈密顿-雅可比微分方程,再用傅里叶级数展开,得到能量:
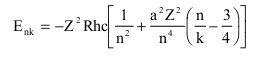
1920年他进一步对碱金属的谱线作出解释。索末菲开创的用相对论处理原子问题的方法后来又经过许多人的研究,继续有所进展,但仍然存在许多障碍,例如光谱强度问题、反常塞曼效应问题等等,看来根本的出路在于建立一套适合于微观体系的崭新理论,靠修补是无济于事的。在这里,要说明一个重要问题。不论是普朗克、威尔逊、石原纯还
相关文章
教育新鲜事
 “超声“和“超音”
“超声“和“超音” 集市一瞥
集市一瞥 昆明湖上
昆明湖上 背道而驰
背道而驰