麦克斯韦速度分布律
麦克斯韦(James Clerk Maxwell,1831—1879)发现气体分子速度分布律是分子运动论和统计力学的发展史中的一件大事。他是在1859年开始进行这项工作的,当时他28岁,已是国王学院(King’sCollege)的教授。1855年他开始研究土星卫环的稳定性时,就曾注意到卫环质量的分布问题,他企图用概率理论处理,但是由于问题过于复杂似乎没有希望解决,所以只好放弃。不过他对概率理论的兴趣并未中断。
概率理论的发展要追溯到十九世纪初,1808年,爱尔兰数学家阿德润(R.Adrain,1775—1843)在分析观测数据的误差中,提出了误差分布的两个实例。1823—1828年,德国数学家高斯(C.E.Gauss,1777—1855)对概率理论作了系统论述,推出了正则方程,也叫高斯分布律。到了1835年,天文学家魁泰勒特(L.Quetelet,1796—1874)发表了论述统计理论的专著,他还因擅长于将统计学推广到社会学领域而闻名。1848年麦克斯韦的老师、爱丁堡大学的佛贝斯(Forbes,1815—1854)曾对1767年一次双星观测的统计结果进行过验算,引起了麦克斯韦对概率的兴趣,当时他刚进入爱丁堡大学,年仅17岁。
后来他全面阅读了拉普拉斯(Laplace)等人关于统计学的著作。1850年英国著名物理学家和天文学家赫谢尔(J.F.W.Herschel,1792—1871)在《爱丁堡评论》上发表了长篇述评,介绍魁泰勒特的工作。这篇评论给麦克斯韦强烈印象。1859年4月麦克斯韦偶然地读到了克劳修斯关于平均自由路程的那篇论文,很受鼓舞,重燃了他原来在土星卫环问题上运用概率理论的信念,认为可以用所掌握的概率理论对分子运动论进行更全面的论证。可是在十九世纪中叶,这种新颖思想却与大多数物理学家的观念相抵触。他们坚持把经典力学用于分子的乱运动,企图对系统中所有分子的状态(位置、速度)作出完备的描述。而麦克斯韦认为这是不可能的,只有用统计方法才能正确描述大量分子的行为。他从分子乱运动的基本假设出发得到的结论是:气体中分子间的大量碰撞不是导致象某些科学家所期望的使分子速度平均,而是呈现一速度的统计分布,所有速度都会以一定的几率出现。
1859年麦克斯韦写了《气体动力理论的说明》一文,这篇论文分三部分:第一部分讨论完全弹性球的运动和碰撞,第二部分讨论两类以上的运动粒子相互间扩散的过程,第三部分讨论任何形式的完全弹性球的碰撞。在第一部分他写道①:“如果有大量相同的球形粒子在完全弹性的容器中运动,则粒子之间将发生碰撞,每次碰撞都会使速度变化,所以在一定时间后,活力将按某一有规则的定律在粒子中分配,尽管每个粒子的速度在每次碰撞时都要改变,但速度在某些限值内的粒子的平均数是可以确定的。”接着他用概率方法来求这个速度在某一限值内的粒子的平均数,即速率分布律:“令N为粒子总数,x,y和z为每个粒子速度的三个正交方向的分量。x在x与x+dx之间的粒子数为Nf(x)dx,其中f(x)是x的待定函数;y在y与y+dy之间的粒子数为Nf(y)dy;z在z与z+dz之间的粒子数为Nf(z)dz,这里f始终代表同一函数。”在此他作出了关键性的假设,即由于不断碰撞,粒子三个互相垂直的速度分量互相独立。
他写道:“速度x的存在绝不以任何方式影响速度y与z,因为它们互成直角,并且互相独立,所以速度在x与x+dx,y与y+dy以及z与z+dz之间的粒子数为Nf(x)f(y)f(z)dxdydz.如果假设N个粒子在同一时刻由原点出发,则此数将为经过单位时间以后在体积元(dxdydz)内的粒子数,因此单位体积内的粒子数应是Nf(x)f(y)f(z)由于坐标的方向完全是任意的,所以此数仅仅和与原点的距离有关,即
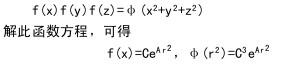
概率理论的发展要追溯到十九世纪初,1808年,爱尔兰数学家阿德润(R.Adrain,1775—1843)在分析观测数据的误差中,提出了误差分布的两个实例。1823—1828年,德国数学家高斯(C.E.Gauss,1777—1855)对概率理论作了系统论述,推出了正则方程,也叫高斯分布律。到了1835年,天文学家魁泰勒特(L.Quetelet,1796—1874)发表了论述统计理论的专著,他还因擅长于将统计学推广到社会学领域而闻名。1848年麦克斯韦的老师、爱丁堡大学的佛贝斯(Forbes,1815—1854)曾对1767年一次双星观测的统计结果进行过验算,引起了麦克斯韦对概率的兴趣,当时他刚进入爱丁堡大学,年仅17岁。
后来他全面阅读了拉普拉斯(Laplace)等人关于统计学的著作。1850年英国著名物理学家和天文学家赫谢尔(J.F.W.Herschel,1792—1871)在《爱丁堡评论》上发表了长篇述评,介绍魁泰勒特的工作。这篇评论给麦克斯韦强烈印象。1859年4月麦克斯韦偶然地读到了克劳修斯关于平均自由路程的那篇论文,很受鼓舞,重燃了他原来在土星卫环问题上运用概率理论的信念,认为可以用所掌握的概率理论对分子运动论进行更全面的论证。可是在十九世纪中叶,这种新颖思想却与大多数物理学家的观念相抵触。他们坚持把经典力学用于分子的乱运动,企图对系统中所有分子的状态(位置、速度)作出完备的描述。而麦克斯韦认为这是不可能的,只有用统计方法才能正确描述大量分子的行为。他从分子乱运动的基本假设出发得到的结论是:气体中分子间的大量碰撞不是导致象某些科学家所期望的使分子速度平均,而是呈现一速度的统计分布,所有速度都会以一定的几率出现。
1859年麦克斯韦写了《气体动力理论的说明》一文,这篇论文分三部分:第一部分讨论完全弹性球的运动和碰撞,第二部分讨论两类以上的运动粒子相互间扩散的过程,第三部分讨论任何形式的完全弹性球的碰撞。在第一部分他写道①:“如果有大量相同的球形粒子在完全弹性的容器中运动,则粒子之间将发生碰撞,每次碰撞都会使速度变化,所以在一定时间后,活力将按某一有规则的定律在粒子中分配,尽管每个粒子的速度在每次碰撞时都要改变,但速度在某些限值内的粒子的平均数是可以确定的。”接着他用概率方法来求这个速度在某一限值内的粒子的平均数,即速率分布律:“令N为粒子总数,x,y和z为每个粒子速度的三个正交方向的分量。x在x与x+dx之间的粒子数为Nf(x)dx,其中f(x)是x的待定函数;y在y与y+dy之间的粒子数为Nf(y)dy;z在z与z+dz之间的粒子数为Nf(z)dz,这里f始终代表同一函数。”在此他作出了关键性的假设,即由于不断碰撞,粒子三个互相垂直的速度分量互相独立。
他写道:“速度x的存在绝不以任何方式影响速度y与z,因为它们互成直角,并且互相独立,所以速度在x与x+dx,y与y+dy以及z与z+dz之间的粒子数为Nf(x)f(y)f(z)dxdydz.如果假设N个粒子在同一时刻由原点出发,则此数将为经过单位时间以后在体积元(dxdydz)内的粒子数,因此单位体积内的粒子数应是Nf(x)f(y)f(z)由于坐标的方向完全是任意的,所以此数仅仅和与原点的距离有关,即
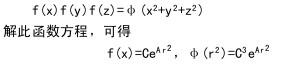
教育新鲜事
 “超声“和“超音”
“超声“和“超音” 集市一瞥
集市一瞥 昆明湖上
昆明湖上 背道而驰
背道而驰