什么时候走长的路比短的路更快?
那么,难道说走折曲的路径比走直线能够更快地到达目的地吗?是的,如果全程各段的行进速度不一样,那情形的确是这样。举例来说,假定有一个人住在两个火车站之间,而离一个火车站很近。他想尽快走到比较远的那个车站上去,他会骑马向反方向走到比较近的车站,在那里搭上火车到他的目的地去。从他的村庄到他的目的地,如果一直骑马前去,走的路会近一些,但是他宁愿骑马搭火车走一段比较长的路,原因是这样走会比较快到达目的地。在这里,走长的路就比走短的路更快。现在不妨再花一分钟时间看一看另外一个例子。
一位骑马的通讯员,要从A点把一份报告送到C点的司令官那里。在他和司令官帐幕之间隔着一片沙地和一片大草地,沙地和草地的分界线是一条直线 EF。马在沙地里走是很困难的,这儿的速度只等于在草地上速度的一半。问:为了尽快把报告送到,这位骑马的通讯员应该选择怎么样的路线?初看最快的路径自然应当是从A到C的直线。但这是完全错误的,而且我也不相信会有走这条路径的通讯员。沙地上难走他是明白的,这使他正确地考虑到难走的沙路应该越短越好,就是越过这沙地的路线应该越斜得少越好;当然,这样做会加长了越过草地上的路;但是在草地上可以走得比较快,速度等于沙地的两倍,因此路长一些也还是有利的,使得全程可以在较短时间里走完。
换句话说,他走的路线应该在沙地和草地的分界线上拆曲,使草原上所走的路线跟分界线的垂线所成的角,比沙地上所走的路线跟这垂线所成的角大。懂几何学的人,可以用勾股弦定理算出直线 AC 果然不是最快的路线,如果照我们这里图上所画的尺寸来说,假定我们沿 AEC 折线行进的话,可以更快到达目的地。图上注明,沙地阔2公里,草地阔3公里,BC长7公里。于是按照勾股弦定理,AC的全长就是


一位骑马的通讯员,要从A点把一份报告送到C点的司令官那里。在他和司令官帐幕之间隔着一片沙地和一片大草地,沙地和草地的分界线是一条直线 EF。马在沙地里走是很困难的,这儿的速度只等于在草地上速度的一半。问:为了尽快把报告送到,这位骑马的通讯员应该选择怎么样的路线?初看最快的路径自然应当是从A到C的直线。但这是完全错误的,而且我也不相信会有走这条路径的通讯员。沙地上难走他是明白的,这使他正确地考虑到难走的沙路应该越短越好,就是越过这沙地的路线应该越斜得少越好;当然,这样做会加长了越过草地上的路;但是在草地上可以走得比较快,速度等于沙地的两倍,因此路长一些也还是有利的,使得全程可以在较短时间里走完。
换句话说,他走的路线应该在沙地和草地的分界线上拆曲,使草原上所走的路线跟分界线的垂线所成的角,比沙地上所走的路线跟这垂线所成的角大。懂几何学的人,可以用勾股弦定理算出直线 AC 果然不是最快的路线,如果照我们这里图上所画的尺寸来说,假定我们沿 AEC 折线行进的话,可以更快到达目的地。图上注明,沙地阔2公里,草地阔3公里,BC长7公里。于是按照勾股弦定理,AC的全长就是

教育新鲜事
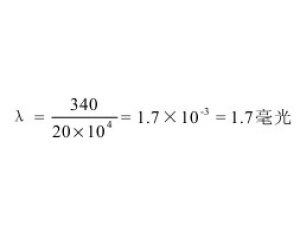 “超声“和“超音”
“超声“和“超音” 集市一瞥
集市一瞥 昆明湖上
昆明湖上 背道而驰
背道而驰