余数是几?
有一列数,它们是1、2、4、7、11、16、22、29、……这列数组成的规律是:第1个数是1,第2个数比第1个数多1,第3个数比第2个数多2,第4个数比第3个数多3,……那么这列数左起第1995个数除以5的余数是几?
分析与解 这列数组成的规律是:第 1个数是1,第2个数比第1个数多1,第3个数比第2个数多2,第4个数比第3个数多3,……也就是说,第1个数是1,第2个数比第1个数多1,第3个数比第1个数多1+2.即多3,第4个数比第1个数多1+2+3,即多6,……那么第1995个数比第1个数多1+2+3+……1994,于是可知第1995个数是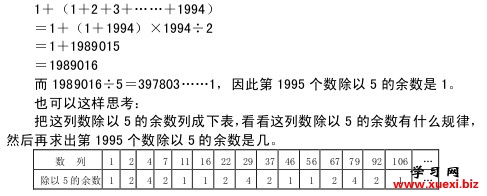
分析与解 这列数组成的规律是:第 1个数是1,第2个数比第1个数多1,第3个数比第2个数多2,第4个数比第3个数多3,……也就是说,第1个数是1,第2个数比第1个数多1,第3个数比第1个数多1+2.即多3,第4个数比第1个数多1+2+3,即多6,……那么第1995个数比第1个数多1+2+3+……1994,于是可知第1995个数是

教育新鲜事
 七根铁链
七根铁链 14÷2≠7吗?
14÷2≠7吗?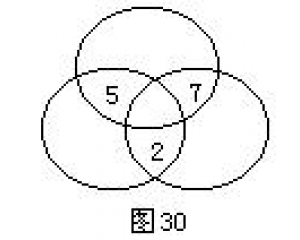 空白处填几?
空白处填几?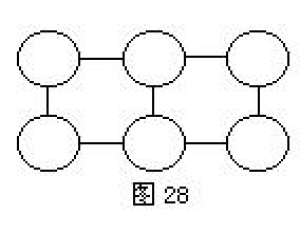 中间的两个圆圈里该填几
中间的两个圆圈里该填几