n3+11n必能被6整除
小朋友，你一定很关心中国科大少年班的同学们，很想知道他们做些什么数学题目吧。我们现在介绍一道少年班的试题，你也来试试看吧。题目：如果n是自然数，n3+11n必能被6整除。
答案：n3＋11n＝n3-n＋12n＝n（n2-1）+12n＝（n-1）·n·（n＋1）＋12n
上式中，12n是6的整倍数，只要考察（n－1）·n·（n＋1）是不是6的整倍数就行了。我们知道n-1，n和n＋1是三个连续自然数。而任何三个连续自然数中，至少有一个是偶数；任何三个连续自然数中，必定有一个是3的倍数，或说“可被3整除”。所以三个连续自然数的乘积可被2与3整除，也可被6整除。12n是可被6整除的。所以n3＋11n也必可被6整除。
答案：n3＋11n＝n3-n＋12n＝n（n2-1）+12n＝（n-1）·n·（n＋1）＋12n
上式中，12n是6的整倍数，只要考察（n－1）·n·（n＋1）是不是6的整倍数就行了。我们知道n-1，n和n＋1是三个连续自然数。而任何三个连续自然数中，至少有一个是偶数；任何三个连续自然数中，必定有一个是3的倍数，或说“可被3整除”。所以三个连续自然数的乘积可被2与3整除，也可被6整除。12n是可被6整除的。所以n3＋11n也必可被6整除。
七根铁链
14÷2≠7吗？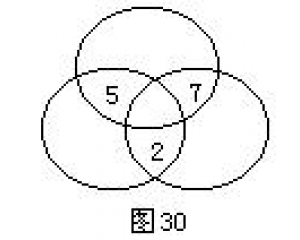
空白处填几？
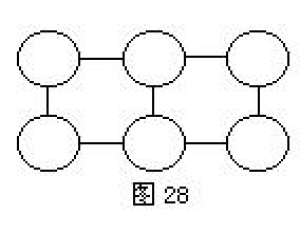中间的两个圆圈里该填几教育新鲜事