机灵的小白鼠
大花猫是捕鼠能手,每天要抓到不少老鼠。但它在吃老鼠以前,先要叫老鼠列队报数。第一批吃掉报单数的;剩下的老鼠重新报数。第二批,花猫仍吃掉报单数的;第三批也是如此……最后剩下的一只老鼠可以被保留,与第二天抓来的老鼠一起重新排队报数。后来,发生了一件极其有趣的事情。
大花猫发现,一连好几天,最后被留下的总是一只机灵的小白鼠。大花猫就问小白鼠:“你想了什么办法,能每天都留下呢?”小白鼠说:“尊敬的大花猫先生,每天排队前我都先数一数你抓到了多少只老鼠,然后,我站在一个相应的位置,就可以留下来了。”大花猫听了小白鼠的详细回答,很感叹地说:“没想到,害人的老鼠里居然也有你这样聪明的小白鼠呀!”
小白鼠行了一个礼,恭敬地说:“尊敬的大花猫先生,不瞒您说,我并不是害人的老鼠,我是从科学家的实验室里溜出来玩的,您放我回去,好吗?”大花猫高兴地放它回去,临别的时候,大花猫还感谢小白鼠给它上了一节生动的数学课呢!你知道吗,小白鼠每天应站在什么位置才能不被花猫吃掉。(为了方便,我们假设第一天共有十只老鼠排队,第二天是二十只,拿出你的算术游戏子来试着排排看吧。)
答案:大花猫第一批吃掉序数是单数的老鼠,留下序数是双数,也就是序数能被2整除的老鼠(如2、8、14、等)。第一批吃完后,2、6、10……这些序数变成1、3、5、……,这样的老鼠在第二批就要被吃掉。而4、8、12……变成2、4、6……这样的序数还能被2整除,第二批就不会被吃掉。所以,如果序数中有尽可能多的因数 2,老鼠就安全了。聪明的小白鼠就专拣这样的位置站。比如10只老鼠排队,站第8个(2×2×2)20只老鼠排队,站第16个(2×2×2×2)作为规律,我们写成:

图片1
我们又遇到了1、2、4、8、……2n这组数字。事实上,如果我们能把某一只老鼠的序数化成二进制数,就立刻可以知道它将在第几批被吃掉了。如第12只老鼠。将12化成二进数是1100,右面第一、二位是“0”所以它在第一批,第二批都留下。而右面第三位出了“1”,它肯定在第三批被吃掉。只有那些序数化成二进制数只有一个“1”和若干个“0”的老鼠,才有可能最后留下。如第4只老鼠,序数化成二进制数是100;第8只是1000;第16只是10000,都符合这些条件,有可能留下。
至于留下这几只中哪一只,要看排队的老鼠多少而定。
大花猫发现,一连好几天,最后被留下的总是一只机灵的小白鼠。大花猫就问小白鼠:“你想了什么办法,能每天都留下呢?”小白鼠说:“尊敬的大花猫先生,每天排队前我都先数一数你抓到了多少只老鼠,然后,我站在一个相应的位置,就可以留下来了。”大花猫听了小白鼠的详细回答,很感叹地说:“没想到,害人的老鼠里居然也有你这样聪明的小白鼠呀!”
小白鼠行了一个礼,恭敬地说:“尊敬的大花猫先生,不瞒您说,我并不是害人的老鼠,我是从科学家的实验室里溜出来玩的,您放我回去,好吗?”大花猫高兴地放它回去,临别的时候,大花猫还感谢小白鼠给它上了一节生动的数学课呢!你知道吗,小白鼠每天应站在什么位置才能不被花猫吃掉。(为了方便,我们假设第一天共有十只老鼠排队,第二天是二十只,拿出你的算术游戏子来试着排排看吧。)
答案:大花猫第一批吃掉序数是单数的老鼠,留下序数是双数,也就是序数能被2整除的老鼠(如2、8、14、等)。第一批吃完后,2、6、10……这些序数变成1、3、5、……,这样的老鼠在第二批就要被吃掉。而4、8、12……变成2、4、6……这样的序数还能被2整除,第二批就不会被吃掉。所以,如果序数中有尽可能多的因数 2,老鼠就安全了。聪明的小白鼠就专拣这样的位置站。比如10只老鼠排队,站第8个(2×2×2)20只老鼠排队,站第16个(2×2×2×2)作为规律,我们写成:

图片1
我们又遇到了1、2、4、8、……2n这组数字。事实上,如果我们能把某一只老鼠的序数化成二进制数,就立刻可以知道它将在第几批被吃掉了。如第12只老鼠。将12化成二进数是1100,右面第一、二位是“0”所以它在第一批,第二批都留下。而右面第三位出了“1”,它肯定在第三批被吃掉。只有那些序数化成二进制数只有一个“1”和若干个“0”的老鼠,才有可能最后留下。如第4只老鼠,序数化成二进制数是100;第8只是1000;第16只是10000,都符合这些条件,有可能留下。
至于留下这几只中哪一只,要看排队的老鼠多少而定。
相关文章
教育新鲜事
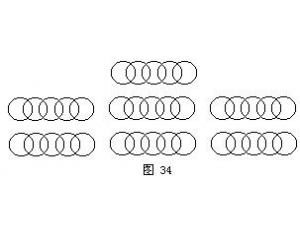 七根铁链
七根铁链 14÷2≠7吗?
14÷2≠7吗?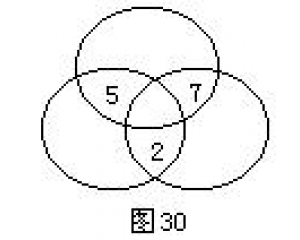 空白处填几?
空白处填几?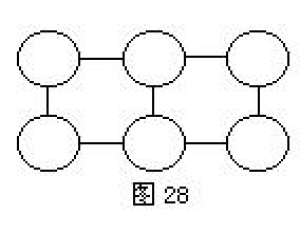 中间的两个圆圈里该填几
中间的两个圆圈里该填几