两头小中间大—正态分布
在测量及实验过程中,我们积累了大量的数据。这些数据的分布,往往呈现两头小、中间大的正态分布的现象。例如某地区,某个年龄段的男人或女人,他们的身高或体重的分布就近似的呈正态分布。例如成年男子超过 2米的极为罕见,超过1.90米的也不多;另一方面不到1.50米和1.60米的也不多,大多数人都在1.65米到1.75米之间。为什么身高服从正态分布呢?原因是影响身高的因素有许多偶然因素,而这些因素相互之间是独立的,再有每一种因素的实际影响都是比较微小的。在这些因素的共同的、随机的作用下形成正态分布。以身高为例,影响它的因素很多,例如父母的身高、个人的营养状况、体育运动的爱好与否、得过什么疾病等等。这些因素中,具备全部有利条件的很少,具备全部不利的条件的也不多,而且大多数人既有长高的条件,也有不利于长高的条件,在这些因素共同作用之下,不高不矮的自然占了多数。它的分布曲线画起来就是一个倒钟形的正态曲线,正态曲线方程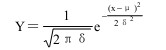
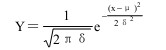
相关文章
教育新鲜事
 分马
分马 龟鹤算
龟鹤算 藏盗法
藏盗法 草纸算术趣题
草纸算术趣题