稀世珍宝

在东京珠宝收藏博览会上展出一棵18K金的圣诞树，在3层塔松形的圣诞树上共镶嵌有1034颗宝石。这棵圣诞树上的宝石是这样摆放的：如果从顶上往下看，3 层圆周上镶嵌的宝石数成等差级数递增；而3层圆锥面的宝石数却按等比级数递增；且第一层的圆周上与圆锥面上的宝石数相等；除此之外，塔松顶上有1颗宝石是独立镶上的。
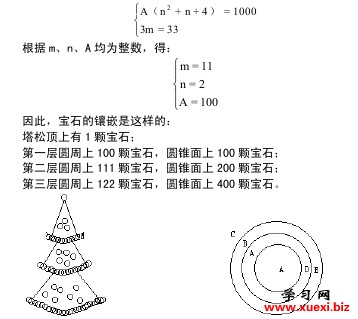
     请问，圣诞树的宝石具体是怎样镶嵌的？解答：假设三层圆周上的宝石数分别为A、B、C，则：B=A+m C=A+2m其中m为等差系数。因为第一层圆锥面上的宝石数等于圆周上的宝石数，所以可假设三层圆锥面上的宝石数为A、D、E，那么：D=nA E=n²A其中：n为等比系数。由于树顶上那颗宝石是独立的，所以：A+B+C+A+D+E+1=1034
     A+A+m+A+2m+A+nA+n²A=1033解此方程，只有一种可能：