蜂窝与太空飞行器
航天飞机、宇宙飞船、人造卫星等太空飞行器,要进入太空持续飞行,就必须摆脱地心引力,这就要求运载它们的火箭必须提供足够大的能量。要把地球上的太空飞行器送到地球大气层外,至少要使该飞行器获得7.9公里/秒的速度,此即第一宇宙速度;而要使飞行脱离地球,飞往行星或其他星球,则需达11.2公里/秒的速度,此谓第二速度。为了使太空飞行器达到上述速度,运载火箭就必须提供相当大的推力。因为运载火箭上带有推进剂、发动机等沉重的“包袱”。按目前航天技术水平,平均发射1公斤重的人造卫星就需要50~100公斤的运载器,反之,太空飞行器自身重量越轻,也就可大大减轻运载火箭身上的“包袱”,也就能使太空飞行器飞得更高、更远。为减轻太空飞行器的重量,科学家们绞尽脑汁,与太空飞行器“斤斤计较”。可要减轻飞行器重量,还要考虑不能减轻其容量与强度。科学家们尝试了许多办法都无济于事,最后,还是蜂窝的结构帮助科学家解决了这个难题。
大家都知道,蜜蜂的窝都是由一些一个挨一个,排列得整整齐齐的六角小蜂房组成的。18世纪初,法国学者马拉尔琪测量到蜂窝的几个角都有一定的规律:钝角等于109°28′。锐角等于70°32′,后来经过法国物理学家列奥缪拉、瑞士数字家克尼格、苏格兰数学家马克洛林先后多次的精确计算,得出如下结论:消耗最少的材料,制成最大的菱形容器,它的角度应该是109°28′和70°32′,和蜂房结构完全一致。但如果从正面观察蜂窝,蜂房是由一些正六边形组成的,既然如此,那每一个角都应是120°,怎么会有109°28′和70°32′呢?这是因为,蜂房不是六棱柱,而是底部由三个菱形拼成的“尖顶六棱柱形”。
我国数学家华罗庚经精确计算指出:在蜜蜂身长、腰周确定情况下,尖顶六棱柱形蜂房用料最省。蜂窝的这种结构特点不正是太空飞行器结构所要求的吗?于是,在太空飞行器中采用了蜂窝结构,先用金属制造成蜂窝,然后再用两块金属板把它夹起来就成了蜂窝结构。这种结构的飞行器容量大,强度高,且大大减轻了自重,也不易传导声音和热量。因此,今天的航天飞机、宇宙飞船、人造卫星都采用了这种蜂窝结构。科学发展就是如此,有时看起来高不可攀的难题,只要开动脑筋,善于从日常生活中觅取线索,可能就会迎刃而解。小小的蜂窝,似乎与伟大的航空航天事业风马牛不相及,但仿生学却将它们紧密地联系在了一起,推动了人类社会的发展与科技的进步。
大家都知道,蜜蜂的窝都是由一些一个挨一个,排列得整整齐齐的六角小蜂房组成的。18世纪初,法国学者马拉尔琪测量到蜂窝的几个角都有一定的规律:钝角等于109°28′。锐角等于70°32′,后来经过法国物理学家列奥缪拉、瑞士数字家克尼格、苏格兰数学家马克洛林先后多次的精确计算,得出如下结论:消耗最少的材料,制成最大的菱形容器,它的角度应该是109°28′和70°32′,和蜂房结构完全一致。但如果从正面观察蜂窝,蜂房是由一些正六边形组成的,既然如此,那每一个角都应是120°,怎么会有109°28′和70°32′呢?这是因为,蜂房不是六棱柱,而是底部由三个菱形拼成的“尖顶六棱柱形”。
我国数学家华罗庚经精确计算指出:在蜜蜂身长、腰周确定情况下,尖顶六棱柱形蜂房用料最省。蜂窝的这种结构特点不正是太空飞行器结构所要求的吗?于是,在太空飞行器中采用了蜂窝结构,先用金属制造成蜂窝,然后再用两块金属板把它夹起来就成了蜂窝结构。这种结构的飞行器容量大,强度高,且大大减轻了自重,也不易传导声音和热量。因此,今天的航天飞机、宇宙飞船、人造卫星都采用了这种蜂窝结构。科学发展就是如此,有时看起来高不可攀的难题,只要开动脑筋,善于从日常生活中觅取线索,可能就会迎刃而解。小小的蜂窝,似乎与伟大的航空航天事业风马牛不相及,但仿生学却将它们紧密地联系在了一起,推动了人类社会的发展与科技的进步。
相关文章
教育新鲜事
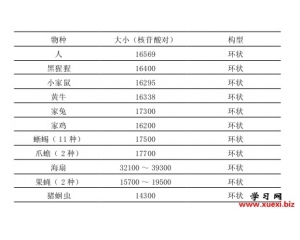 微型的基因组
微型的基因组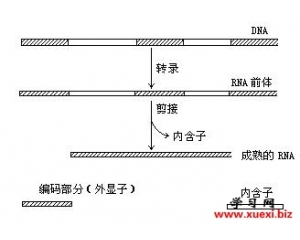 分子生物学的兴起与达尔
分子生物学的兴起与达尔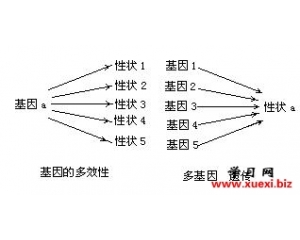 达尔文主义再度突飞猛进
达尔文主义再度突飞猛进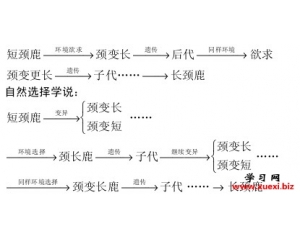 两种进化学说的争论
两种进化学说的争论