非线性过程和耗散结构
通过前述可知,任一过程的描述可以通过该过程引起的通量和驱动力的特征来实现,即热力学通量和驱动力可以用来表征体系偏离热力学平衡的程度。显然,根据偏离热力学平衡的程度可以把体系划分为三种类型:
(1)通量和驱动力皆为零,体系处于平衡态,只能经受可逆过程,适用于孤立体系或封闭体系;(2)通量和驱动力皆不为零的开放体系,边界条件迫使体系离开平衡态,于是发生宏观不可逆过程,此时,如果热力学驱动力很弱,体系偏离平衡态不远,通量与驱动力之间满足线性关系,体系处于非平衡态的线性区;(3)当热力学驱动力不是很弱时,体系远离热力学平衡态,此时热力学通量是驱动力的非线性函数,体系处于非平衡态的非线性区。
下面介绍非线性非平衡态热力学的基本概念,着重讨论远离平衡态的体系的热力学稳定性理论,由此导出耗散结构的概念。非平衡态的非线性区与线性区的一个重要差别在于:后者是接近平衡态的,因此不论该体系演化的动力学机制如何,其演化过程总是单向地趋于平衡态或者在一定程度上类似于平衡态的非平衡的定态,可以用热力学位函数σ或Φ来表征。而对于远离平衡态的非线性非平衡体系没有这些热力学位函数,不再具有普适性的演化规律。此时体系的演化结果取决于动力学过程的具体行为——机制。在非平衡态的非线性区,由于熵密度产生率和耗散函数不具有极值行为,最小耗散原理不再成立。
此时一个体系的稳定性不能从熵产生率或耗散函数来判断。为此假定存在某种热力学位函数,可以用这种位函数的行为来判断非平衡态的非线性区的稳定特性。由于体系的演化过程是用动力学方程来描述的,体系的某种特定的状态则相当于动力学方程(常微分方程或偏微分方程)的某个特解,因此对体系某种特定状态的稳定性的分析(物理的)归结为微分方程的特解的稳定性的讨论(数学的)。根据Lyapounov关于非线性方程的解的稳定性理论,对于微分方程组:


(1)通量和驱动力皆为零,体系处于平衡态,只能经受可逆过程,适用于孤立体系或封闭体系;(2)通量和驱动力皆不为零的开放体系,边界条件迫使体系离开平衡态,于是发生宏观不可逆过程,此时,如果热力学驱动力很弱,体系偏离平衡态不远,通量与驱动力之间满足线性关系,体系处于非平衡态的线性区;(3)当热力学驱动力不是很弱时,体系远离热力学平衡态,此时热力学通量是驱动力的非线性函数,体系处于非平衡态的非线性区。
下面介绍非线性非平衡态热力学的基本概念,着重讨论远离平衡态的体系的热力学稳定性理论,由此导出耗散结构的概念。非平衡态的非线性区与线性区的一个重要差别在于:后者是接近平衡态的,因此不论该体系演化的动力学机制如何,其演化过程总是单向地趋于平衡态或者在一定程度上类似于平衡态的非平衡的定态,可以用热力学位函数σ或Φ来表征。而对于远离平衡态的非线性非平衡体系没有这些热力学位函数,不再具有普适性的演化规律。此时体系的演化结果取决于动力学过程的具体行为——机制。在非平衡态的非线性区,由于熵密度产生率和耗散函数不具有极值行为,最小耗散原理不再成立。
此时一个体系的稳定性不能从熵产生率或耗散函数来判断。为此假定存在某种热力学位函数,可以用这种位函数的行为来判断非平衡态的非线性区的稳定特性。由于体系的演化过程是用动力学方程来描述的,体系的某种特定的状态则相当于动力学方程(常微分方程或偏微分方程)的某个特解,因此对体系某种特定状态的稳定性的分析(物理的)归结为微分方程的特解的稳定性的讨论(数学的)。根据Lyapounov关于非线性方程的解的稳定性理论,对于微分方程组:


教育新鲜事
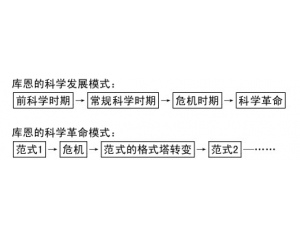 “复式”化学革命模式
“复式”化学革命模式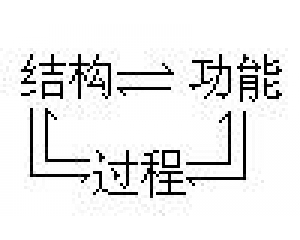 结构、过程与功能的相互
结构、过程与功能的相互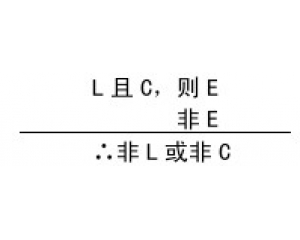 检验的复杂性
检验的复杂性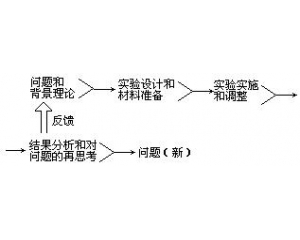 实验操作的程序
实验操作的程序