中考数学这15个重要考点一定要掌握!
对应角相等,对应边成比例的三角形叫做相似三角形。相似用符号“∽”来表示,读作“相似于”。相似三角形对应边的比叫做相似比(或相似系数)。
考点1 相似三角形的基本定理
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
考点2三角形相似的判定
1、三角形相似的判定方法
①、定义法:对应角相等,对应边成比例的两个三角形相似
②、平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似
③、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。
④、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。
⑤、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似
考点3直角三角形相似的判定方法
①、以上各种判定方法均适用
②、定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似
③、垂直法:直角三角形被斜边上的高分成的两个直角三角形与原三角形相似
考点4向量的定义:
既有方向又有大小的量叫做向量。
向量的表示:
具有方向的线段叫做有向线段,以A为起点,B为终点的有向线段记作。
考点5平面向量的种类
有向线段包含3个因素:起点、方向、长度。
①相等向量:长度相等且方向相同的向量叫做相等向量。
②平行向量、共线向量:两个方向相同或相反的非零向量叫做平行向量或共线向量,在向量中共线向量就是平行向量,(这和直线不同,直线共线就是同一条直线了,而向量共线就是指两条是平行向量)
③零向量:长度等于0的向量叫做零向量,记作0。(实数“0”和向量“0”是有区别的,书写时要在实数“0”上加箭头,以免混淆)
零向量的方向是任意的;且零向量与任何向量都平行且垂直。
向量a、b平行,记作a//b,零向量与任意向量平行,即0//a。
④单位向量:模等于1个单位长度的向量叫做单位向量。
考点6向量的线性运算(加、减、数乘):
例如:向量加法的三角形法则。(首尾相连,连接首尾,指向终点)
向量加法的平行四边形法则。(共起点,对角连)。
向量加法的平行四边形法则。
对于零向量和任意向量a,有:0+a=a+0=a。
||a|-|b||≤|a+b|≤|a|+|b|。
向量的加法满足所有的加法运算定律。
考点7:概率统计的知识框架
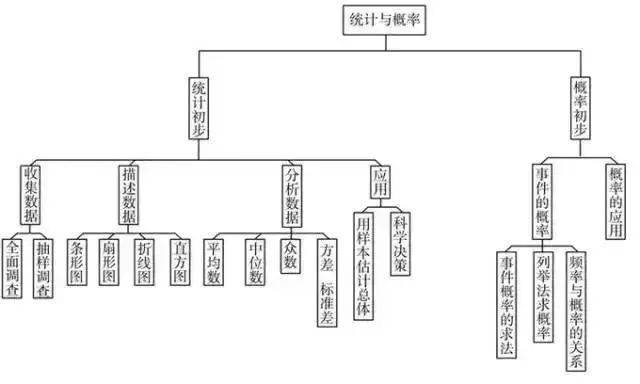
考点8:注意以下几种常见情况
(1)注意概率、机会、频率的共同点和不同点。
(2)注意题目中隐含求概率的问题。
(3)画树状图及其它方法求概率。
(4)摸球模型题注意放回和不放回。
(5)注意在求概率的问题中寻找替代物,常见的替代物有:球,扑克牌,骰子等。
考点9:二次函数的三种表达式
一般式:y=ax^2+bx+c(a,b,c为常数,a≠0)
顶点式:y=a(x-h)^2+k [【抛物线的顶点P(h,k)】
交点式:y=a(x-x?)(x-x?) [仅限于与x轴有交点A(x? ,0)和 B(x?,0)的抛物线]
注:在3种形式的互相转化中,有如下关系:
h=-b/2a k=(4ac-b^2)/4a x?,x?=(-b±√b^2-4ac)/2a
考点10:会画二次函数的图像
在平面直角坐标系中作出二次函数y=x^2的图像,可以看出,二次函数的图像是一条抛物线。
考点11:抛物线的性质
1.抛物线是轴对称图形。对称轴为直线 x = -b/2a。
2.抛物线有一个顶点P,坐标为:P ( -b/2a,(4ac-b^2)/4a )当-b/2a=0时,P在y轴上;当Δ= b^2-4ac=0时,P在x轴上。
3.二次项系数a决定抛物线的开口方向和大小。
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口。|a|越大,则抛物线的开口越小。
4.一次项系数b和二次项系数a共同决定对称轴的位置。
当a与b同号时(即ab>0),对称轴在y轴左;
当a与b异号时(即ab<0),对称轴在y轴右。
5.常数项c决定抛物线与y轴交点。
抛物线与y轴交于(0,c)
6.抛物线与x轴交点个数
Δ= b^2-4ac>0时,抛物线与x轴有2个交点。
Δ= b^2-4ac=0时,抛物线与x轴有1个交点。
Δ= b^2-4ac<0时,抛物线与x轴没有交点。X的取值是虚数(x= -b±√b^2-4ac的值的相反数,乘上虚数i,整个式子除以2a)
考点12: 二次函数与一元二次方程
特别地,二次函数(以下称函数)y=ax^2+bx+c,当y=0时,二次函数为关于x的一元二次方程(以下称方程),即ax^2+bx+c=0
此时,函数图像与x轴有无交点即方程有无实数根。函数与x轴交点的横坐标即为方程的根。
考点13: 垂径定理定义及推论:
(1)垂直于弦的直径平分弦且平分弦所对的弧。
(2)推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
考点14: 集合形式的概念:
1、 圆可以看作是到定点的距离等于定长的点的集合;
2、圆的外部:可以看作是到定点的距离大于定长的点的集合;
3、圆的内部:可以看作是到定点的距离小于定长的点的集合
考点15:轨迹形式的概念:
1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;
2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);
3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;
4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;
5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
考点16:点与圆的关系
点在圆上、点在圆外、点在圆内
圆在中考中所占的比重大概在20%左右,比例相对较多,在填空题、选择题和解答题中都会涉及到,需要大家着重复习。
相关文章
- 中考数学最易出错的61个知识点,赶快收藏!
- 中考数学选填压轴题专题十 选择填空方法综述
- 技巧丨中考数学最常出现的题型有哪些,你知道吗?赶快来看
- 中考数学复习千万要注意这20个字,不要因马虎而丢分!
- 中考数学最易出错的61个知识点,赶快收藏!!
- 中考数学压轴题——依据特征构造最值问题
- 【中考数学】平行四边形的性质知识点总结
- 中考数学这15个重要考点一定要掌握,再不看就来不及了!!
- 2019中考数学重难点分析与梳理,现在看还来得及!
- 中考数学考试涵盖考点超不过28个!赶快来看看都有哪些!
- 中考数学专题复习:直线与圆的位置关系
- 中考数学最易出错的61个知识点,你必须记住!
- 中考数学这几个考点一定要吃透,不然中考必定吃亏!!
- 中考数学:重点知识点大全!
- 中考数学:做题技巧“顺口溜”,错过后悔!
- 【知识点】中考数学5大易错点:提前避开,中考110+绝不是问题!
- 【知识点】中考数学九个几何模型,看了轻松搞定中考!
- 中考数学压轴题:9种题型+5种策略,一篇全面攻破
- 中考数学知识点总结几何篇,2018中考生必备
- 【知识点】中考数学几何知识点总结!
推荐内容
教育新鲜事
 初中生必须吃透的28个数
初中生必须吃透的28个数 初中数学 | 三角形知识
初中数学 | 三角形知识 中考数学最易出错的61个
中考数学最易出错的61个 中考数学选填压轴题专题
中考数学选填压轴题专题