高中数学单调性与最值怎么求,一文全弄懂!
一、情景问题
如图为2008年北京奥运会奥林匹克公园场馆自动气象站某日一天24小时内的气温变化图(24时与0时气温相同为32?C),观察这张气温变化图:
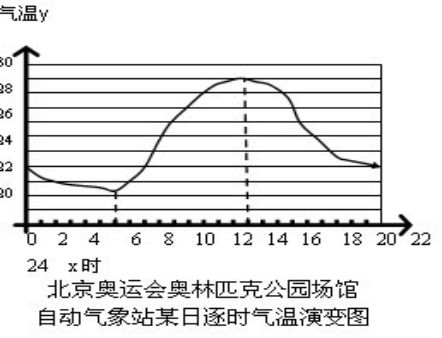
问:该图形是否为函数图象?定义域是什么?
问:如何用数学语言来刻画温度随时间变化而变化的趋势呢?
画出函数f(x)=x和f(x)=x2的图象
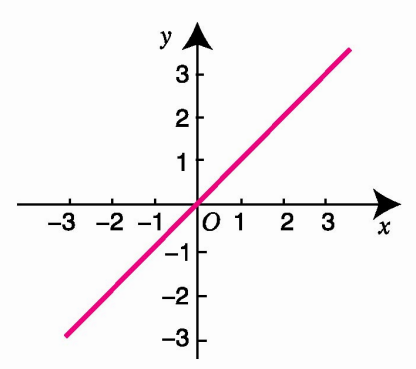
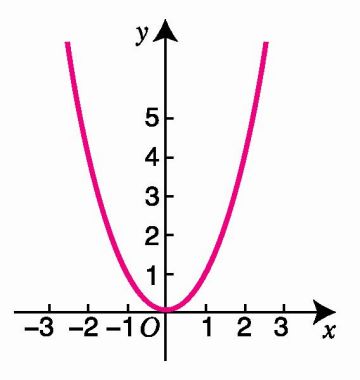
可观察到的图象特征: (1)函数f(x)=x的图象由左至右是上升的;
(2)函数f(x)=x2的图象在y轴左侧是下降的,在y轴右侧是上升的;也就是图象在区间(-∞,0]上,随x着的增大,相应的f(x) 随着减小,在区间(0,+∞)上,随着x的增大,相应的f(x)也随着增大.
归纳:从上面的观察分析可以看出:不同的函数,其图象的变化趋势不同,同一函数在不同区间上的变化趋势也不同.函数图象的这种变化规律就是函数性质的反映.
思考:
1.如何用函数解析式f(x)=x2描述“随着x的增大,相应的f(x)随着减小”,“随着x的增大,相应的f(x)也随着增大”?
2.在区间(0,+∞)上任取x1,x2,函数值的大小变化与自变量的大小变化有何关系?如何用数学符号语言来描述这种关系呢?
对于函数f(x)=x2 ,
在区间(0,+∞)上,任取两个x1,x2,当x1 x2时,有f(x1) f(x2).这时,我们就说函数f(x)=x2在区间(0,+∞)上是增函数.
请你仿照刚才的描述,说明函数f(x)=x2在区间(-∞,0)上是减函数.
对于函数f(x)=x2 ,
在区间(0,+∞)上,任取两个x1,x2,当x1![]() x2时,有f(x1)
x2时,有f(x1) ![]() f(x2).这时,我们就说函数
f(x2).这时,我们就说函数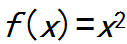 在区间(0,+∞)上是增函数.
在区间(0,+∞)上是增函数.
一、函数的单调性
1.增函数的定义
设函数f(x)的定义域为I:
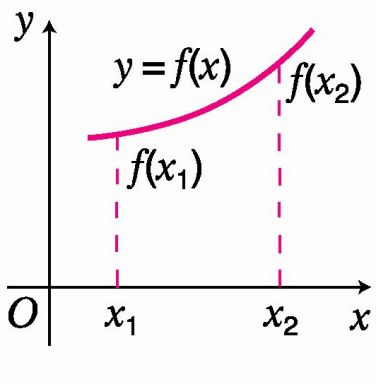
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是增函数(increasing function).
2.减函数的定义
设函数f(x)的定义域为I:
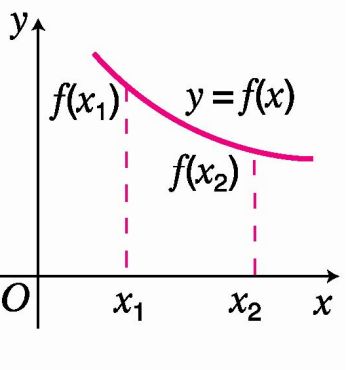
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是减函数(decreasing function).
3.对定义要点分析
1) 函数是增函数还是减函数,是对定义域内某个区间而言的;
2)应是该区间内任意的两个实数,忽略需要任意取值这个条件,就不能保证函数是增函数(或减函数).
3)如果函数y=f(x)在某一区间D上是增(减)函数,就说f(x)在这个区间D上具有单调函数,
这一区间D叫做f(x)的单调区间.
说明:
(1)函数的单调区间D是其定义域I的子集;
(2)判断函数的单调性的方法:
比较法(要注意变形的程度)
(3)证明函数的单调性的步骤:

(1)增减函数的图象有什么特点?增函数的图象从左自右是上升的,减函数的图象从左自右是下降的.
(2)用定义证明函数的单调性,需要抓住要点“在给定区间任意取两个自变量”去比较它们的函数值的大小.
(3)如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.







相关文章
- 高中数学“函数”必考知识点及常考题型总结
- 【高中数学】《三角函数》“诱导公式”大汇总
- 高中数学最容易出错的十道函数经典例题,快来巩固吧!
- 高中数学十大抢分技巧讲解,选择题正确率低的一定要看!(附赠得
- 高中数学立体几何知识点锦集,涵盖高中所有知识点,火速打印!
- 高中数学--大题的超棒解题技巧及解题思路!
- 高中数学最容易丢分的66个易混点,高中生赶紧收!
- 高中数学公式大全 高考文科必背数学公式整理
- 【数学】高中数学8大模块考试答题思路与模版
- 一招制胜! 高中数学想上130? 必须练会这些“破题神功“!
- 高中数学必修:三角函数知识点归纳,三角函数题型再不丢分!
- 高中数学:结构图汇总,几乎涵盖所有知识点。。。
- 高中数学必背公式总结 2019高考数学必背重点公式大全
- 高中数学必考300道经典难题, 刷完稳过一本线!(可下载)
- 高中数学如何由弱转强?掌握这12种解题思路,秒变数学学霸!
- 高中数学:数列求和的方法
- 高中数学:椭圆焦半径的几种求解方法
- 高中数学:不同分数段的学生有不同的提分窍门,这才是真经!
- 高中数学归纳法在证明不等式中的应用题型总结
- 高中数学:求切点弦所在直线方程的方法
推荐内容
教育新鲜事
 高中数学“函数”必考知
高中数学“函数”必考知 高考数学答题方法的19条
高考数学答题方法的19条 高考数学干货丨最容易出
高考数学干货丨最容易出 【高中数学】《三角函数
【高中数学】《三角函数