考前必看 | 高中物理必修一知识点汇总+习题解析

1. 如图所示，在粗糙水平地面上放着一个截面为半圆的柱状物体A，A与竖直墙之间放一光滑半圆球B，整个装置处于静止状态。已知A、B两物体的质量分别为mA和mB，则下列说法正确的是(　　)

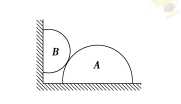
A.A物体对地面的压力大小为mAg

B.A物体对地面的压力大小为(mA＋mB)g

C.B物体对A物体的压力大于mBg

D.地面对A物体没有摩擦力

【答案】　BC

【解析】　对B物体受力分析，如图甲所示，根据合力等于0，运用合成法，得墙壁对B的弹力FN1＝mBgtan α，A对B的弹力FN2＝cos αmBg＞mBg，结合牛顿第三定律，B物体对A物体的压力大于mBg，C正确；对整体受力分析，如图乙所示，地面的支持力FNA＝(mA＋mB)g，摩擦力Ff＝FN1＝mBgtan α≠0，A、D错误，

2. 如图所示，用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂，小球处于静止状态，弹簧A与竖直方向的夹角为30°，弹簧C水平，则弹簧A、C的伸长量之比为(　　)

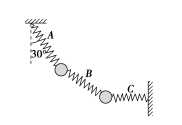
A.∶4

B.4∶

C.1∶2

D.2∶1

【答案】 D

【解析】把两个小球看成整体，分析受力，由平衡条件可得：FAsin 30°＝FC，又FA＝kxA，FC＝kxC，联立解得弹簧A、C的伸长量之比xA∶xC＝1∶sin 30°＝2∶1，选项D正确。

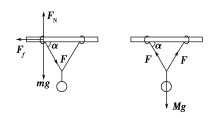
3. 如图所示，在一根粗糙的水平直杆上套有两个质量均为m的铁环，两铁环上系着两根等长细线，共同拴住质量为M的小球，两铁环与小球都处于静止状态．现想办法使得两铁环间距离增大稍许而仍能保持系统平衡，则水平直杆对铁环的支持力FN和摩擦力Ff的可能变化是(　　)．

A．FN不变　

B．FN增大

C．Ff增大　

D．Ff不变

【答案】 AC

【解析】　对铁环和小球受力分析如图所示，以整体为研究对象，2FN＝Mg＋2mg，可见FN与α角无关，即FN不变，A对，B错；摩擦力Ff＝Fcos α，2Fsin α＝Mg，所以，所以说Ff随着α角的减小而增大，C对，D错．

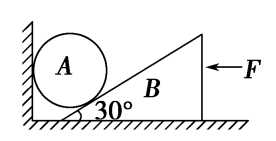
4. 如图所示，球A重G1＝60 N，斜面体B重G2＝100 N，斜面倾角为30°，一切摩擦均不计．则水平力F为多大时，才能使A、B均处于静止状态？此时竖直墙壁和水平面受到的压力各为多大？

【答案】　20 N　20N　160 N

【解析】　方法一　(隔离法)　分别对A、B进行受力分析，建立直角坐标系如图甲、乙所示，由共点力平衡条件可得

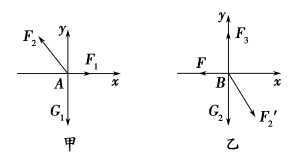
对A有F2sin 30°＝F1，F2cos 30°＝G1

对B有F＝F2′sin 30°，F3＝F2′cos 30°＋G2

其中F2和F2′是一对相互作用力，即F2＝F2′

代入数据，联立解得F＝F1＝20N，F3＝160 N

由牛顿第三定律可知，竖直墙壁和水平面受到的压力分别为20 N、160 N.