高考物理:破解带电粒子在磁场中的匀速圆周运动
总是抱怨带电粒子在复合场中的模型掌握不好,那小编就来给大家把确定轨迹的方法总结一下吧!
处理带电粒子在匀强磁场中的圆周运动问题,其本质是平面几何知识与物理知识的综合运用。重要的是正确建立完整的物理模型,画出准确、清晰的运动轨迹。
“带电粒子在磁场中的圆周运动”的基本型问题
找圆心、画轨迹是解题的基础,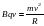 是解题的“灵魂”,学会找带电粒子做匀速圆周运动的圆心、求出半径,再进一步求其它物理量就不难了。
是解题的“灵魂”,学会找带电粒子做匀速圆周运动的圆心、求出半径,再进一步求其它物理量就不难了。
1.圆心与轨迹确定
带电粒子进入一个磁场后的轨道是一段圆弧,如何确定圆心是解决问题的前提,也是解题的关键,而圆心一定在与速度方向垂直的直线上。
在实际问题中圆心位置的确定极为重要,通常有三个方法:
(1)如图1所示,图中P为入射点,M为出射点,已知入射方向和出射方向时,可以通过入射点和出射点作垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧轨道的圆心O。
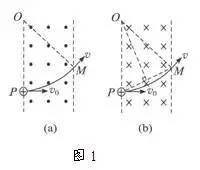
(2)图2所示,图中A为入射点,B为出射点,已知入射方向和出射点的位置时,可以通过入射点做入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨道的圆心O。
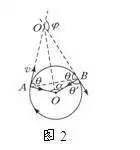
(3)圆心与轨迹的确定又常常借助于“圆的几何对称规律”
如从同一边界射入的粒子,又从同一边界射出时,速度与边界的夹角一定相等(图3);在圆形磁场区域内,沿径向射入的粒子,必沿径向射出(图4)。
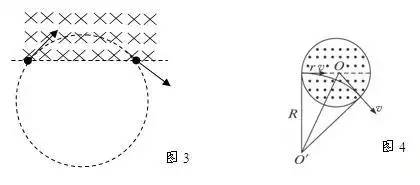
2.半径的计算
一般利用几何知识解直角三角形。
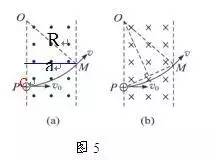
如图5中,已知有界磁场的宽度为a,带电粒子离开磁场时方向改变了30°,求粒子的轨道半径。
由直角三角形函数关系得:R=asin30°。
若并不知粒子离开磁场的偏转角,而知道入射点与出射点相距b,则利用直角三角形关系,R2=a2+(R-c)2,c2=b2-a2,由此可求R。
3.运动时间的确定
先求周期T,再求出粒子运动这部分圆弧是整个圆周的几分之几,再求时间t。
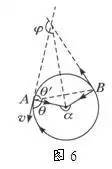
如图6所示,要求粒子从A运动到B的时间,粒子在洛伦兹力作用下做匀速圆周运动,不论沿顺时针方向还是逆时针方向,从A点运动到B点,粒子速度偏向角(φ)等于圆心角(回旋角α)并等于AB弦与切线的夹角(弦切角θ)的2倍,即:φ=α=2θ=ωt.
利用圆心角(回旋角α)与弦切角θ的关系,或者利用四边形内角和等于360°计算出圆心角α的大小,由公式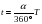 可求出粒子在磁场中的运动时间。
可求出粒子在磁场中的运动时间。
练习
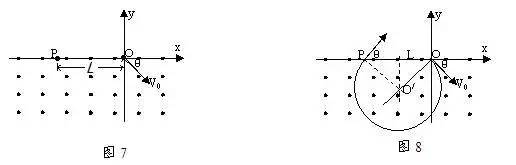
如图7在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸面外,磁场的磁感应强度为B;一带正电的粒子以速度V0从O点射入磁场中,入射方向在xy平面内,与x轴正方向的夹角为θ;若粒子射出磁场的位置与O点的距离为L。求①该粒子的电荷量和质量比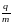 ;②粒子在磁场中的运动时间。
;②粒子在磁场中的运动时间。
解:由图8可知粒子圆周运动的几何关系有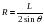 。
。
再由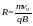 ,解之
,解之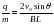 。
。
如图8知粒子在磁场中转过的圆心角为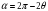 ,
,
故粒子在磁场中的运动时间为 .
.
规律总结:
带电粒子在匀强磁场中做匀速圆周运动的程序解题法——三步法
(1)画轨迹:确定圆心,画出运动轨迹用几何方法求半径。
(2)找联系:轨道半径与磁感应强度、运动速度相联系,偏转角度与圆心角、运动时间相联系,在磁场中运动的时间与周期相联系。
(3)用规律:即牛顿第二定律和圆周运动的规律,特别是周期公式、半径公式。
相关文章
- 物理丨高考物理5大类型的实验要点整理
- 高考物理中5种发现隐含条件的方法!
- 【高考物理】记住高中物理常用的快速推论,做题事半功倍!
- 【高考物理】力学部分最易错易混十大知识点汇总,务必牢记!
- 高考物理经典六大常考题型梳理汇总,拿下就是高分!
- 高考物理难点:单摆知识详解及例题分析!实用!
- 高考物理:机械能守恒定律的8大考点!
- 高考物理难重点:力学部分最易错易混的十大知识点全解析!
- 【高考物理】力学实验、电学实验必考重点归纳
- 【物理】高考物理经典6大常考题型梳理汇总
- 高考物理冲刺必备25个考点解析汇总!
- 高考物理复习必备公式大全总结,还不赶紧收藏?
- 高考物理:《选修3-5》必考点大全,学习重点都在这里!
- 精品干货 | 搞定高考物理这16个纠错笔记,物理轻松拿高分!
- 【高考物理】知识点归纳:动量
- 真题汇编 | 带电粒子在磁场中的运动 最近几年真题汇编,快做做看
- 高考物理选修3-2知识点汇总,收藏贴
- 知识干货 | 高考物理必考公式汇总
- 干货 | 高考物理公式汇总!赶紧收藏~
- 高考物理:易错题型大全,高中必考!
推荐内容
教育新鲜事
 【高考物理】记住高中物
【高考物理】记住高中物 高考物理经典六大常考题
高考物理经典六大常考题 高考物理难点:单摆知识
高考物理难点:单摆知识 高考物理:机械能守恒定
高考物理:机械能守恒定