八年级上册数学一次函数复习资料

变量与函数

　　一、知识回顾

　　1、变量：在一个变化过程中可以取不同数值的量，函数中用x表示。

　　常量：在一个变化过程中只能取同一数值的量，往往用c来表示。

　　2、函数：一般的，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就把x称为自变量，把y称为因变量，y是x的函数。

　　3、定义域：一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域。

　　4、函数的解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做函数的解析式

　　5、函数的图像

　　一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象．

　　6、函数的表示方法

　　（1）列表法：一目了然，使用起来方便，但列出的对应值是有限的，不易看出自变量与函数之间的对应规律。

　　（2）解析式法：简单明了，能够准确地反映整个变化过程中自变量与函数之间的相依关系，但有些实际问题中的函数关系，不能用解析式表示。

　　（3）图象法：形象直观，但只能近似地表达两个变量之间的函数关系。

　　二、典型例题

　　例1：骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化．在这一问题中，自变量是（　　）

　　          A．沙漠                     B．体温                      C．时间                    D．骆驼

　　分析：因为骆驼的体温随时间的变化而变化，符合“对于一个变化过程中的两个量x和y，对于每一个x的值，y都有唯一的值和它相对应”的函数定义，自变量是时间．

　　解答：∵骆驼的体温随时间的变化而变化，

　　          ∴自变量是时间；

　　          故选C．

  _________________________________________________________________________________________

　　例2：在圆的周长公式C=2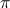r中，变量是________,________,常量是________.

　　分析：根据函数的意义可知：变量是改变的量，常量是不变的量，据此即可确定变量与常量．

　　解答：∵在圆的周长公式C=2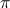r中，C与r是改变的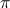，是不变的；

　　          ∴变量是C，r，常量是2．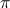

  _________________________________________________________________________________________

　　例3．下列各曲线中，不能表示y是x的函数的是（　　）

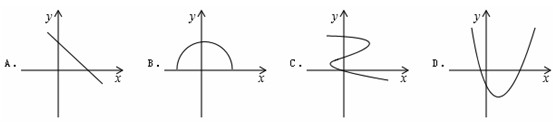
　　分析：根据函数是一一对应的关系，给自变量一个值，有且只有一个函数值与其对应，就是函数，如果不是，则不是函数．

　　解答：在A、B、D、选项的图上任意取一点，做垂直于x的直线，发现只有一个交点，故正确。而C选项、很明显，不止一个交点，不是一一对应关系，所以不是函数，错误；

　　          故选C

  _________________________________________________________________________________________

　　例4：下列解析式中，y不是x的函数是（　　）

　　          A．y+x=0                     B．|y|=2x                     C．y=|2x|                     D．y=2x²+4

　　分析：本题需利用函数的定义解决问题．

　　解答：因为在|y|=2x中，若x=2，y就有2个值与其对应，所以y不是x的函数．

　　          故选B．

  _________________________________________________________________________________________

　　例5：下列函数中，与y=x表示同一个函数的是（　　）

　　分析：函数y=x中，自变量x和函数值y均可取任意实数，判断两个函数是不是同一个函数，关键看它们的定义域和值域是不是一样。依次分析四个选项，自变量和函数值均可取任意实数的为正确答案．

　　解答：A、x不能为0；

　　          B、y不能为负数；

　　          C、y不能为负数；

　　          D、正确．

　　          故本题选D．

  _________________________________________________________________________________________

　　例6：点（2，-1）在下列函数图象上的是（　　）

　　          A．y=2x                          B．y=x²-3                           C．y=-x+1                           D．y=2x-1

　　分析：判断点在不在函数图象上，不需要画图，只需要把点的坐标带入函数关系式即可，如果等式成立，点就满足这个函数就在函数图象上，反之不在。

　　解答：A、y=2 2 =1≠-1，故本选项错误；

　　          B、y=22-3=1≠-1，故本选项错误；

　　          C、y=-2+1=-1，故本选项正确；

　　          D、y=2×2-1=3≠-1，故本选项错误．

　　          故选：C．

  _________________________________________________________________________________________

　　例7：一长方形的周长为20厘米，则它的长x厘米与宽y厘米之间的关系是:_________

　　分析：根据长方形的另一边长=周长的一半-一边长，把相关数值代入即可求解．

　　解答：∵长方形的周长是20厘米，一边长为x厘米，

　　          ∴长方形的另一边长=20/2 -x=10-x，

　　          ∴它的长x厘米与宽y厘米之间的关系是：y=10-x；

　　          故填：y=10-x．

  _________________________________________________________________________________________

　　分析：根据分式、二次根式有意义的条件列出关于x的不等式，通过解不等式求得x的取值范围，然后将其表示在数轴上即可．

　　解答：根据题意，得：

　　          6-2x＞0，

　　          解得x＜3；

　　          在数轴上表示为：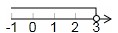 

　　          故选B．

  _________________________________________________________________________________________

　　例9：（2012·南充）在函数: 中，自变量x的取值范围是（　　）

　　          A．x≠1/2                     B．x≤1/2                     C．x＜1/2                      D．x≥1/2

　　分析：根据被开方数大于等于0，分母不等于0列式计算即可得解．

　　解答：根据题意得，1-2x≥0且x-1/2 ≠0，

　　          解得x≤1/2 且x≠1/2 ，

　　          所以x＜1/2 ．

　　          故选C．

　　三、解题经验

　　本节重点是理解函数的概念，具体理解方法在“函数知识点整理”中有。我们在判断图像是不是函数图像时的依据是“一一对应关系”。判断点在不在函数图象上时，依据是直接把点带入到函数关系式中，如果等式成立则满足。判断是不是表示同一个函数时，只需要判断定义域和值域，如果相同，则表示的是同一个函数。

变量与函数2

　　一、知识回顾

　　1、定义域：x的取值范围。一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域。

　　常见的情况：①：根号下面的≥0；②：分母≠0；③：有指数时，底数≠0

　　2、值域：y的取值范围。一般情况下根据x的取值来判定。

　　二、典型例题

　　例1：求下列函数中自变量x的取值范围（定义域）

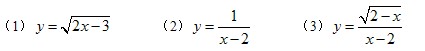
　　分析：（1）函数关系中主要有二次根式．根据二次根式的意义，被开方数是非负数即可求解．

　　          （2）根据分母不等于0列式计算即可得解．

　　          （3）根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．

　　解答：（1）根据题意得：2x-3≥0，

　　                    解得x≥3/2 ．

　　          （2）根据题意得，x-2≠0，

　　                    解得x≠2．

　　          （3）根据题意得：2-x≥0且x-2≠0，

　　                    解得：x≤2且x≠2，即x＜2．

　　          故选D．

     _____________________________________________________________________________________________

　　例2：下图中，分别给出了变量x与y之间的对应关系，y不是x的函数的是（　　）

　　分析：函数的意义反映在图象上简单的判断方法是：做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点．

　　解答：根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，所以D不正确．

　　          故选D．

     _____________________________________________________________________________________________

　　例3：下列图象不表示y是x的函数的是（　　）

　　分析：根据函数的定义可知：对于x的任何值y都有唯一的值与之相对应．做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点．由此很容易就能得出结论。

　　解答：解：根据函数的定义可知，只有B不能表示函数关系．

　　          故选B．

     _____________________________________________________________________________________________

　　例4：下面的表格列出了一个实验的统计数据，表示将皮球从高处落下时，弹跳高度b与下降高度d的关系，下面能表示这种关系的式子是（　　）:

　　          A．b=d²                     B．b=2d                     C．b=d/2                     D．b=d+25

　　分析：这是一个用图表表示的函数，可以看出d是b的2倍，即可得关系式．

　　解答：由统计数据可知：

　　          d是b的2倍，

　　          所以，b=d² ．

　　          故本题选C．

　　三、解题经验

　　求函数中自变量x的取值范围时，通常有这几种情况：

　　（1）当函数表达式是整式时，自变量可取全体实数；

　　（2）当函数表达式是分式时，考虑分式的分母不能为0；

　　（3）当函数表达式是二次根式时，被开方数为非负数．

　　判断图像是不是函数图象的方法是：做垂直x轴的直线在左右平移的过程中如果始终只有一个交点，那么就是函数图象，反之不是。

一次函数的定义

  
　　一、知识回顾

　　1、一次函数：形如y=kx+b (k≠0, k, b为常数)的函数。

　　注意：（1）要使y=kx+b是一次函数，必须k≠0。如果k＝0，则kx＝0，y=kx+b就不是一次函数；

　　           （2）当b=0时，y=kx，y叫x的正比例函数。

　　2、正比例函数：形如y=kx（k为常数，且k≠0）的一次函数，那么y就叫做x的正比例函数。 正比例函数属于一次函数，但一次函数却不一定是正比例函数。

　　二、典型例题

　　例1：（2006?武汉）下列函数：①y=x；②y=x/4 ；③y=4/x ；④y=2x+1，其中一次函数的个数是（　　）

　　　　   A．1　　   　　   B．2 　　   　　   C．3 　　   　　   D．4

　　分析：根据一次函数的定义条件进行逐一分析即可．注意：一个单项式中,所有字母的指数的和叫做这个单项式的次数

　　解答：①y=x是一次函数；

　　　　   ②y=x/4 是一次函数；

　　　　   ③y=4/x ，两边同时乘以x得到：xy=4，是二次，故不是一次函数；

　　　　   ④y=2x+1是一次函数．

　　　　   故选C．

    ___________________________________________________________________________________________

　　例2：函数y=（m-2）^xn-1+n是一次函数，m，n应满足的条件是（　　）

　　　　   A．m≠2且n=0 　　   　　   B．m=2且n=2  　　   　　    C．m≠2且n=2  　　   　　   D．m=2且n=0

　　分析：根据一次函数的定义列出方程组解答即可．一次函数固然最高次项为1，并且x的系数不能为0，为0就没有未知数了。

　　解答：∵函数y=（m-2）x^n-1+n是一次函数，

　　　　   ∴{ m-2≠0

　　　　   { n-1=1    解得： m≠2 ，n=2

　　　　   故选C．

   ___________________________________________________________________________________________

　　例3：一次函数y=-2x-1，当x=-5时，y=________,当y=-7时，x=________．

　　分析：直接将x=-5和y=7分别代入解析式即可求解．

　　解答：把x、y的值分别代入一次函数y=-2x-1，

　　　　   当x=-5时，y=-2×（-5）-1=9；

　　　　   当y=-7时，-7=-2x-1，解得x=3．

　　　　   故填9、3．

   ___________________________________________________________________________________________

　　例4：列说法正确的是（　　）

　　　　   A．y=kx+b（k、b为任意常数）一定是一次函数　　   B．y=x/k （常数k≠0）不是正比例函数

　　　　   C．正比例函数一定是一次函数 　　 　　   　　          D．一次函数一定是正比例函数

　　分析：根据一次函数和正比例函数的定义条件进行逐一分析即可．

　　解答：A、y=kx+b（k、b为任意常数），当k=0时，不是一次函数，故本选项错误；

　　　　   B、y=x/k （常数k≠0）是正比例函数，故本选项错误；

　　　　   C、正比例函数一定是一次函数，故本选项正确；

　　　　   D、一次函数不一定是正比例函数，故本选项错误．

　　　　   故选C．

　　三、解题经验

　　本节知识点比较简单，理解了函数的概念后，很容易就能掌握一次函数的概念。如果题目中明确告诉是一次函数，那么最高次数就必定为1，并且x的系数不为0.

一次函数的图像

　　

　　一、知识回顾

　　1、图象的位置:

                   

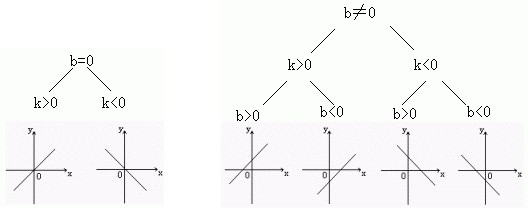
　　总结：当k＞0时，函数图象向上爬；k＜0时，函数图像向下滑。

　　          当b＞0时，函数图象交y轴上半轴；b＜0时，函数图象交y轴下半轴。

　　二、典型例题

　　例1：画出函数y=2x的图像。

　　分析：根据画图步骤：取点，描点，连线，三步就能画出函数图象，一般情况下取对称点，并且数字较小。

　　解答：

　　          第一步：取点，（一般情况下，取以0为中心的点）

                                

　　          第二步：描点，（根据坐标知识准确标出上面取的点）

                                

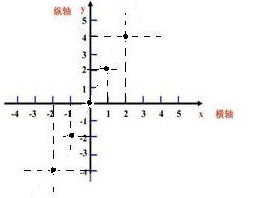
　　          第三步：连线，（用平滑的线连接起来）

                                

_________________________________________________________________________________________

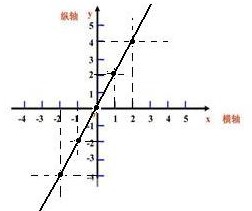
　　例2：（2011·清远）一次函数y=x+2的图象大致是（　　）

                    

　　分析：根据一次函数y=x+2与x轴和y轴的交点，结合一次函数图象的性质便可得出答案．

　　解答：解：一次函数y=x+2，当x=0时，y=2；当y=0时，x=-2，

　　          故一次函数y=x+2图象经过（0，2）（-2，0）；

　　          故根据排除法可知A选项正确．

　　          故选A．

_________________________________________________________________________________________

　　例3：（2010·贵阳）一次函数y=kx+b的图象如图所示，当y＜0时，x的取值范围是（　　）

                 

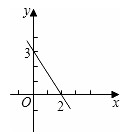
　　          A．x＞0                     B．x＜0                     C．x＞2                     D．x＜2

　　分析：根据函数图象可知，此函数为减函数，图象与x轴的交点坐标为（2，0），由此可得出答案．

　　解答：根据图象和数据可知，当y＜0即直线在x轴下方时，x的取值范围是x＞2．

　　          故选C．

_________________________________________________________________________________________

　　例4：y=kx+k的大致图象是（　　）

                 

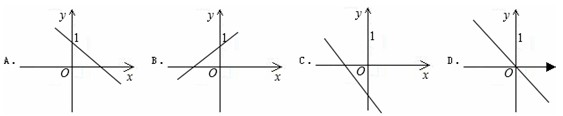
　　分析：根据图象经过的象限确定k的取值范围，然后判断．

　　解答：根据图象知：

　　          A、k＜0；k＞0．解集没有公共部分，所以不可能；

　　          B、k＞0；k＞0．解集有公共部分，但是k不一定为1；

　　          C、k＜0；k＜0．解集有公共部分，所以有可能；

　　          D、k＜0；k=0．解集没有公共部分，所以不可能，

　　          则符合题意的选项为C．

　　          故选C．

_________________________________________________________________________________________

　　例5：一次函数y=mx+2与正比例函数y=2mx（m为常数，且m≠0）在同一坐标系中的图象的是（　　）

                 

　　分析：因为m的符号不明确，所以应分两种情况讨论，找出符合任意条件的选项即可．

　　解答：分两种情况：

　　          1、当m＞0时，一次函数y=mx+2经过第一、二、三象限；正比例函数y=2mx过原点、第一、三象限，无选项符合；

　　          2、当m＜0时，一次函数y=mx+2经过第一、二、四象限；正比例函数y=2mx过原点、第二、四象限，选项A符合．

　　          故选A．

_________________________________________________________________________________________

　　例6：下列表示一次函数y=mx-n与正比例函数y=mnx（m、n为常数，且mn≠0）图象中，一定不正确的是（　　）
                   

　　分析：根据一次函数与正比例函数的性质对四个选项进行逐一分析即可．

　　解答：A、由一次函数的图象可知，m＜0，-n＞0，故n＜0，mn＞0；由正比例函数的图象可知mn＜0，两结论相矛盾，故本选项错误；

　　          B、由一次函数的图象可知，m＜0，-n＞0，故n＜0，mn＞0；由正比例函数的图象可知mn＞0，两结论一致，故本选项正确；

　　          C、由一次函数的图象可知，m＞0，-n＞0，故n＜0，mn＜0；由正比例函数的图象可知mn＜0，两结论一致，故本选项正确；

　　          D、由一次函数的图象可知，m＞0，-n＜0，故n＞0，mn＞0；由正比例函数的图象可知mn＞0，两结论一致，故本选项正确．

　　故选A．

　　三、解题经验

　　掌握函数图象的画法至关重要，后面用得非常广泛。掌握函数的几种表示方法。

一次函数的性质

  
  
　　一、知识回顾

　　1、一次函数的增减性

　　k>0时，y随x增大而增大

　　k<0时，y随x增大而减小

　　二、典型例题

　　例1：一次函数y₁=kx+b与y₂=x+a的图象如图，则下列结论：①k＜0；②a＞0；③当x＞2时，y2＞y1，其中正确的个数是（　　）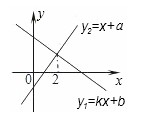

　　          A．0                       B．1                     C．2                     D．3

　　分析：根据一次函数的性质求解．

　　解答：一次函数y₂=x+a的图像向上爬，并且轴交于y的负半轴，所以a＜0

　　          一次函数y₁=kx+b的图象向下滑，∴k＜0，并且交于y的正半轴，所以b＞0，

　　          当x＞2时，y₂的图像永远在y1的上方，∴y₂＞y₁，①③正确．

　　          故选C．

     __________________________________________________________________________________________

　　例2：已知一次函数y=kx+b，其中kb＞0．则所有符合条件的一次函数的图象一定通过（　　）

　　          A．第一、二象限                        B．第二、三象限

　　          C．第三、四象限                        D．第一、四象限

　　分析：根据题意，kb＞0，则k、b同号，分k＞0与k＜0情况讨论，分别判断其图象所过的象限，综合可得答案．

　　解答：根据题意，kb＞0，则k、b同号，

　　          当k＞0时，b＞0，此时函数图象过一二三象限，

　　          当k＜0时，b＜0，此时函数图象过二三四象限，

　　          综合可得，所有符合条件的一次函数的图象一定通过第二、三象限，

　　          故选B．

     __________________________________________________________________________________________

　　例3：（2012·泉州）若y=kx-4的函数值y随x的增大而增大，则k的值可能是下列的（　　）

　　          A．-4                     B．-1/2                     C．0                     D．3

　　分析：若y随x的增大而增大，则k必须大于0，由此可知k的范围。

　　解答：∵y=kx-4的函数值y随x的增大而增大，

　　          ∴k＞0，

　　          而四个选项中，只有D符合题意，

　　          故选D．

     __________________________________________________________________________________________

　　例4：（2011·遵义）若一次函数y=（2-m）x-2的函数值y随x的增大而减小，则m的取值范围是（　　）

　　          A．m＜0                     B．m＞0                     C．m＜2                      D．m＞2

　　分析：函数值y随x的增大而减小，说明k小于0，图像向下滑。由此列出式子。

　　解答：∵一次函数y=（2-m）x-2的函数值y随x的增大而减小，

　　          ∴2-m＜0，

　　          ∴m＞2．

　　          故选D．

     __________________________________________________________________________________________

　　例5：直线y=1/2 x+k与x轴y轴的交点分别为A、B，如果S△AOB≤1，那么k的取值范围是（　　）

　　          A．k≤1                      B．0＜k≤1                         C．-1≤k≤1                     D．k≤-1或k≥1

　　分析：先求出直线y=1/2 x+k与x轴y轴的交点分别为A、B，得到OA，OB的长，利用三角形的面积公式得到不等式，对照选项进行判断．

　　解答：令x=0，则y=k，得B（0，k）；

　　          令y=0，则x=-2k，得A（-2k，0），

　　          所以OA=|2k|，OB=|k|，S△AOB=1/2×|2k|×|k|=k²≤1，

　　          所以-1≤k≤1．

　　          故选C．

     __________________________________________________________________________________________

　　例6：正比例函数y=ax中，y随x的增大而增大，则直线y=（-a-1）x经过（　　）

　　          A．第一、三象限                     B．第二、三象限

　　          C．第二、四象限                     D．第三、四象限

　　分析：根据正比例函数的增减性，可得a＞0；则-a-1＜0，据此判断直线y=（-a-1）x经过的象限．

　　解答：∵正比例函数y=ax中，y随x的增大而增大，

　　          ∴a＞0，

　　          ∴-a-1＜0，

　　          ∴直线y=（-a-1）x经过第二、四象限．

　　          故选C．

     __________________________________________________________________________________________

　　例7：（2009·衢州）P₁（x₁，y₁），P₂（x₂，y₂）是正比例函数y=-x图象上的两点，则下列判断正确的是（　　）

　　          A．y₁＞y₂                                         B．y₁＜y₂

　　          C．当x₁＜x₂时，y₁＞y₂                   D．当x₁＜x₂时，y₁＜y₂

　　分析：根据正比例函数图象的性质可知．

　　解答：根据k＜0，得y随x的增大而减小．

　　          故选C．

　　例8：已知正比例函数y=kx．

　　          （1）若函数图象经过第二、四象限，则k的范围是什么？

　　          （2）点（1，-2）在它的图象上，求它的表达式．考点：正比例函数的性质．专题：待定系数法．

　　分析：（1）根据正比例函数图象的性质，得k＜0；

　　          （2）只需把点的坐标代入即可计算．

　　解答：（1）∵函数图象经过第二、四象限，

　　                   ∴k＜0；

　　          （2）当x=1，y=-2时，则k=-2，

　　                   即：y=-2x．

     __________________________________________________________________________________________

　　例9：已知函数y=（m+1）x+m-1

　　          （1）若这个函数的图象经过原点，求m的值；

　　          （2）若这个函数的图象经过第一、三、四象限，求m的取值范围；

　　          （3）画出（1）中函数的图象．考点：一次函数的图象；一次函数的性质．专题：计算题；作图题．

　　分析：（1）若函数的图象经过原点，则当x=0时，y=0，代入解析式，可得m的值，

　　           （2）若函数的图象经过第一、三、四象限，根据一次函数图象的性质，可得m+1＞0，m-1＜0，解可得答案，

　　          （3）在（1）中，m=1时，函数的解析式为y=2x，进而可作出函数的图象．

　　解答：（1）若函数y=（m+1）x+m-1的图象经过原点，

　　                   则当x=0时，y=0，

　　                   将其代入解析式，可得0=m-1，

　　                   即m=1，

                 （2）若函数的图象经过第一、三、四象限，

　　                   则m+1＞0，m-1＜0，

　　                   解可得-1＜m＜1，

　　          （3）在（1）中，m=1时，函数的解析式为y=2x，

　　                   图象过原点与（1，2），据此可以作出函数的图象．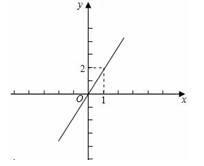

　　三、解题经验

　　任何函数都存在增减性，一次函数的增减性较为简单，一定要牢记于心。综合性强的题目要求对知识的系统掌握，我们在学习是过程中，一定要系统学习，并且善于总结。

一次函数的解析式

  
　　一、知识回顾

　　1、把y=kx+b（k≠0，b为常数）叫做一次函数的标准解析式，简称标准式。

　　2、设y=kx+b中的k，b，最终求得他们的值，叫做待定系数；用此方法求一次函数的解析式叫用待定系数法求一次函数的解析式。

　　二、典型例题

　　例1：若A（0，2），B（-2，1），C（6，a）三点在同一条直线上，则a的值为（　　）

　　           A．-2                         B．-5                         C．2                          D．5

　　分析：三点在一条直线上，所以这个图像可以用一次函数的表达式来描述，设直线的解析式是y=kx+b，把A（0，2），B（-2，1）代入得到方程组，求出方程组的解即可得出直线的解析式，把C的坐标代入即可求出答案．

　　解答：设直线的解析式是y=kx+b．

　　           把A（0，2），B（-2，1）代入得： {2=b
　　                                                                    {1=-2k+b

　　           解得：k=1/2 ，b=2，

　　           ∴y=1/2 x+2，

　　           把C（6，a）代入得：a=5，

　　           故选D．

____________________________________________________________________________________________

　　例2：一条直线通过A（2,6），B（-1,3）两点，求此直线的解析式。

　　分析：题目中明确告知是一条直线，我们知道一次函数的图像是一条直线，所以“求此直线的解析式”，就是求这个一次函数的表达式，通过待定系数法来求。

　　解答：设：此直线的解析式为：y=kx+b（k≠0，b为常数），根据题意得：

　　           { 6=2k+b   ①
　           　{ 3=-k+b   ②

　　解得：k=1，b=4

　　           故这条直线的解析式为：y=x+4

____________________________________________________________________________________________

　　例3：若点A（2，4）在直线y=kx-2上，则k=（　　）

　　           A．2                       B．3                       C．4                       D．0

　　分析：点A在直线y=kx-2，说明点A的坐标满足关系式y=kx-2，把点的坐标代入此关系式，即可求出k值．

　　解答：根据题意：2k-2=4，

　　           解得k=3．

　               故选B．

____________________________________________________________________________________________

　　例4：已知点M（4，3）和N（1，-2），点P在y轴上，且PM+PN最短，则点P的坐标是（　　）

　　           A．（0，0）                        B．（0，1）                       C．（0，-1）                       D．（-1，0）

　　分析：两点之间线段最短，先把画出N点关于Y轴的对称点Q，然后确定MQ的解析式，最后命x=0，即可求出纵坐标。

　　解答：将N关于y轴对称到第三象限得Q(-1,-2)则PM+PN=PM+PQ

　　           两点之间线段最短；P点即为直线MQ与y轴的交点

　　           直线MQ：y=x-1则P为(0,-1)。  故选C

____________________________________________________________________________________________

　　例5：如图，已知一次函数y=kx+b的图象经过A（0，1）和B（2，0），当x＞0时，y的取值范围是（　　）

　　           A．y＜1                       B．y＜0                       C．y＞1                       D．y＜2

　　分析：观察图象可知，y随x的增大而减小，而当x=0时，y=1，根据一次函数的增减性，得出结论．

　　解答：把A（0，1）和B（2，0）两点坐标代入y=kx+b中，得

　　           b=1/2k+b=0   ，解得 k=-1/2 ， b=1

　　           ∴y=-1/2 x+1，

　　           ∵-1/2 ＜0，y随x的增大而减小，

　　           ∴当x＞0时，y＜1．

　　           故选A．

____________________________________________________________________________________________

　　例6：已知一次函数y=kx+b的图象如图所示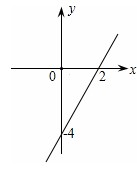

　　           （1）当x＜0时，y的取值范围是______。

　　           （2）求k，b的值．

　　分析：（1）由图得，当x=0时，y=-4，所以，当x＜0时，y＜-4；

　　           （2）函数图象过（2，0）和（0，-4）两点，代入可求出k、b的值；

　　解答：（1）由图得，当x＜0时，y＜-4；

                  （2）由图可得：函数图象过（2，0）和（0，-4）两点，

　　                    代入得， { 2k+b=0   ①
　　                                    { b=-4        ②

　　           解得：k=2，b=-4，

　　           故答案为k=2，b=-4．

____________________________________________________________________________________________

　　例7：一次函数y=kx+4的图象经过点（-3，-2），则

　　           （1）求这个函数表达式；

　　           （2）建立适当坐标系，画出该函数的图象；

　　           （3）判断（-5，3）是否在此函数的图象上；

　　           （4）把这条直线向下平移4个单位长度后的函数关系式是__________

　　分析：（1）待定系数法即可求解；

　　           （2）根据函数解析式即可画出图象；

　　           （3）把点代入即可判断是否在直线解析式上；

　　           （4）根据上加下减的规律即可得出答案；

　　解答：解：（1）∵一次函数y=kx+4的图象经过点（-3，-2），

　                          　∴-3k+4=-2，

　　                       　∴k=2，

　　                       　∴函数表达式y=2x+4；

　　                  （2）图象如图：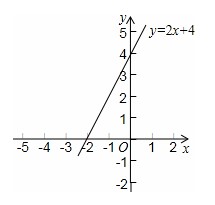

　　                  （3）把（-5，3）代入y=2x+4，

　　                       　∵-10+4=-6≠3，

　　                       　∴（-5，3）不在此函数的图象上；

　　                  （4）∵把这条直线向下平移4个单位，

　　                       　∴函数关系式是：y=2x；

　　                       　故答案为：y=2x．

　　三、解题经验

　　我们观察一次函数的解析式y=kx+b发现，有两个未知数k，b，所以必须要两个方程才能求出k，b，用待定系数法求一次函数解析式时，我们要用心搜集信息，最常见的是知道两个点，然后代入解析式即可。

　　判断点A在不在一次函数图像上，只需把A点的坐标代入解析式即可，如果满足等式，即在图像上，反之不在。

一次函数与一元一次方程

　　一、知识回顾

　　1、一次函数：形如y=kx+b (k≠0, k, b为常数)的函数。

　　2、一元一次方程：只有一个未知数，并且最高次数为一的等式叫一元一次方程

　　3、对比一次函数y=kx+b，和一元一次方程 kx+b=0，发现一次函数的函数值为0时的x值就是方程的解。

　　二、典型例题

　　例1：（2012·济南）一次函数y=kx+b的图象如图所示，则方程kx+b=0的解为（　　）

                       

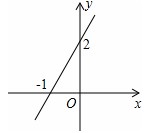
　　          A．x=2                     B．y=2                     C．x=-1                     D．y=-1

　　分析：函数图像与x轴的交点（函数值y＝0）时kx+b=0，此时的x的值就是方程的解。

　　解答：∵一次函数y=kx+b的图象与x轴的交点为（-1，0），

　　          ∴当kx+b=0时，x=-1．

　　          故选C．

    _______________________________________________________________________________________

　　例2：（2010·梧州）直线y=2x+b与x轴的交点坐标是（2，0），则关于x的方程是2x+b=0的解是__________。

　　分析：本题可以画图来解，很直观，方法如上题；也可以根据直线y=2x+b与x轴的交点坐标是（2，0），求得b，再把b代入方程2x+b=0，求解即可．

　　解答：把（2，0）代入y=2x+b，

　　          得：b=-4，把b=-4代入方程2x+b=0，

　　          得：x=2．

　　          故填2．

    _______________________________________________________________________________________

　　例3：关于一次函数y=-2x+2有结论：①当x＞1时，y＜0；②图像经过第一、二、三象限；③图像经过点（-1，4）；④图像可以由函数y=-2x的图象向上平移2个单位得到．其中正确的结论有（　　）

　　          A．1个                     B．2个                     C．3个                     D．4个

　　分析：当x=1时，可得y=0，而k=-2＜0，y随x的增大而减小，可判断①正确；

　　          根据一次函数y=kx+b（k≠0）的性质可判断②不正确；

　　          把点（-1，4）代入一次函数的解析式即可判断③正确；

　　          根据直线平移k不变，可得到函数y=-2x的图象向上平移2个单位得到的图象解析式为y=-2x+2，于是判断④正确．

　　解答：当x=1时，y=-2+2=0，k=-2＜0，y随x的增大而减小，则当x＞1时，y＜0，所以①正确；

　　          对于y=-2x+2，k=-2＜0，图象经过第二、四象限，又b=2＞0，图象与y轴的交点在x轴上方，所以图象经过第一、二、四象限，所以②不正确；

　　          当x=-1，y=-2×（-1）+2=4，所以图象经过点（-1，4），所以③正确；

　　          函数y=-2x的图象向上平移2个单位得到的图象解析式为y=-2x+2，所以④正确．

　　          故选C．

    _______________________________________________________________________________________

　　例4：已知一次函数y=kx-3，图象如图所示，A、B两点分别为图象与x轴、y轴的交点．

                 

　　          （1）求此函数的解析式；

　　          （2）求A、B两点的坐标．

　　分析：（1）将点（2，-1）代入一次函数y=kx-3可得k的值，继而可得出函数解析式．

　　          （2）分别令x=0，y=0可得出B和A的坐标．

　　解答：（1）由图象可函数过点（2，-1）可得：k=1．

　                   　∴此函数的解析式为：y=x-3．

　　          （2）令x=0得：y=-3

　　                  令y=0得：x=3

　　                 ∴A（3，0），B（0，-3）

　　三、解题经验

　　始终记住，当一次函数的图像与x轴交点处就是函数值y=0时，此时通一次函数的方程的解，就是交点的横坐标。解本节题目一定要数形结合。

一次函数与一元一次不等式

  
　　一、知识回顾

　　1、一次函数：形如y=kx+b (k≠0, k, b为常数)的函数。

　　2、用不等符号连接起来的称为不等式，不等式的解大多是一个范围。

　　3、观察一次函数的图像可知，图像不管是向上爬还是向下滑，始终分为三个阶段，函数值大于0，等于0，小于0，这三个阶段对于的x值往往是常考点。

　　二、典型例题

　　例1：已知一次函数y=ax+b（a、b是常数），x与y的部分对应值如下表：下列说法中，错误的是（　　）

　　          A．方程ax+b=0的解是x=-1                                    B．不等式ax+b＞0的解集是x＞-1

　　          C．y=ax+b的函数值随自变量的增大而增大            D．y=ax+b的函数值随自变量的增大而减小

　　分析：把图中任意两组对应值代入一次函数y=ax+b，求得a，b的值再解答．

　　解答：由题意得{ -4=-3a+b   ①
　　                         { -2=-2a+b    ②，解得 a=2 b=2

　          　函数的解析式为y=2x+2，

　　          A、方程ax+b=0，即2x+2=0的解是x=-1，正确；

          
　　          B、不等式ax+b＞0，即2x+2＞0的解集是x＞-1，正确；

　　          C、y=ax+b的函数值，即y=2x+2的值随自变量的增大而增大，正确；

　　          D、y=ax+b的函数值随自变量的增大而减小，错误．

　　          故选D．

    __________________________________________________________________________________________

　　例2：（2012·阜新）如图，一次函数y=kx+b的图象与y轴交于点（0，1），则关于x的不等式kx+b＞1的解集是（　　）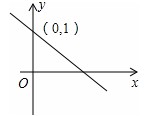

　　          A．x＞0                     B．x＜0                     C．x＞1                     D．x＜1

　　分析：“不等式kx+b＞1”告诉我们要求的是使得函数值y＞1时x 的取值。观察图形。

　　解答：由一次函数的图象可知，此函数是减函数，

　　          ∵一次函数y=kx+b的图象与y轴交于点（0，1），

　　          ∴当x＜0时，关于x的不等式kx+b＞1．

　　          故选B．

    __________________________________________________________________________________________

　　例3：（2011·乐山）已知一次函数y=ax+b的图象过第一、二、四象限，且与x轴交于点（2，0），则关于x的不等式a（x-1）-b＞0的解集为（　　）

　　          A．x＜-1                     B．x＞-1                     C．x＞1                     D．x＜1

　　分析：根据一次函数y=ax+b的图象过第一、二、四象限，得到b＞0，a＜0，把（2，0）代入解析式y=ax+b求出b/a =-2，解a（x-1）-b＞0，得x-1＜b/a ，代入即可求出答案．

　　解答：∵一次函数y=ax+b的图象过第一、二、四象限，

　　          ∴b＞0，a＜0，

　　          把（2，0）代入解析式y=ax+b得：0=2a+b，

　　          解得：b/a =-2，

　　          ∵a（x-1）-b＞0，

　　          ∴a（x-1）＞b，

　　          ∴x-1＜b a ，

　　          ∴x＜-1，

　　          故选A．

    __________________________________________________________________________________________

　　例4：已知一次函数y=kx+b的图象平行于y=-2x+1，且过点（2，-1），求：

　　          （1）这个一次函数的解析式；

　　          （2）当x=1时，y的值，当y=2时，x的值；

　　          （3）画出该一次函数的图象；

　　          （4）根据图象回答：当x取何值时，y＞0；y=0；y＜0？

　　分析：（1）根据题意，设这个一次函数的解析式为y=-2x+b，又由过点（2，-1），代入y=-2x+b，代入可得b的值，即可得到答案；

　　          （2）在（1）求得的解析式中，令x=1和y=2，求得对应的y（x）的值，可得答案；

　　          （3）由（1）求得的解析式中，以及（2）所得的特殊点，作出图象即可；

　　          （4）观察图象，可得答案．

　　解答：解：（1）根据题意，设这个一次函数的解析式为y=-2x+b，

　　                          又由过点（2，-1），代入y=-2x+b，

　　                          可得b=3，

　　                          则一次函数的解析式为y=-2x+3；

　　                 （2）由（1）得，一次函数的解析式为y=-2x+3，

　　                          当x=1时，y=1，

　　                          当y=2时，x=1//2 ；

　　                 （3）作出图象可得，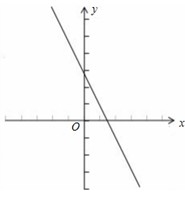

　　                 （4）根据图象可得：当x＜3/2 时，y＞0，

　　                          当x=3/2 时，y=0，

　　                          当x＞3/2 时，y＜0．

　　三、解题经验

　　一次函数y=kx+b的图象的性质：①当k＞0，y的值随x的值增大而增大；②当k＜0，y的值随x的值增大而减小．

　　本节题目大多是综合性题目，包括：对一次函数与一元一次不等式的关系，一次函数的性质，一次函数图象上点的坐标特征，解一元一次不等式等

一次函数与二元一次方程组

　　一、知识回顾

　　1、把y=kx+b（k≠0，b为常数）叫做一次函数的标准解析式，简称标准式。

　　2、求两个一次函数的图像的交点时，只需把两个函数的解析式组成方程组求公共解即可。

　　二、典型例题

　　例1：如图，观察图象，判断下列说法错误的是（　　）

             

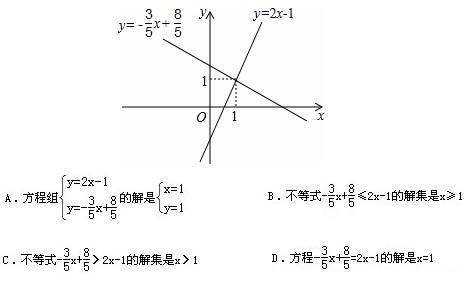
　　分析：根据函数图象，利用函数与方程，不等式的关系即可求解．

　　解答：A、两个函数图像的交点坐标是（1，1），所以他们解析式组成的方程组的解释x=1，y=1，正确。

　　           B、-3/5 x+8/5 ≤ 2x-1说明前面一个函数的图像在后面一个函数的图像下方，观察图像可以得知，当x≥1时才能满足，正确；

　　           C、不等式-3/5 x+8/5 ＞2x-1的解集是：x＜1．

　　           ∴不等式-3/5 x+8/5 ＞2x-1的解集是x＞1的说法错误

　　           D、方程-3/5 x+8/5 = 2x-1表示的是两个函数的函数值相等，我们知道，当两个函数图像交点时函数值相等，正确。

　　           故选C

________________________________________________________________________________________

　　例2：（2012·呼和浩特）下面四条直线，其中直线上每个点的坐标都是二元一次方程x-2y=2的解是（　　）

             

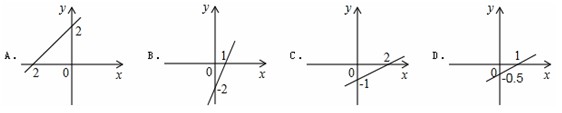
　　分析：根据两点确定一条直线，当x=0，求出y的值，再利用y=0，求出x的值，即可得出一次函数图象与坐标轴交点，即可得出图象．

　　解答：∵x-2y=2，

　　           ∴y=1/2 x-1，

　　           ∴当x=0，y=-1，当y=0，x=2，

　　           ∴一次函数y=1/2 x-1，与y轴交于点（0，-1），与x轴交于点（2，0），

　　           即可得出C符合要求，

　　           故选：C．

________________________________________________________________________________________

　　例3：（2010·聊城）如图，过点Q（0，3.5）的一次函数的图象与正比例函数y=2x的图象相交于点P，能表示这个一次函数图象的方程是（　　）

                    

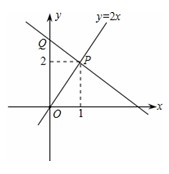
　　           A．3x-2y+3.5=0                       B．3x-2y-3.5=0                       C．3x-2y+7=0                        D．3x+2y-7=0

　　分析：如果设这个一次函数的解析式为y=kx+b，那么根据这条直线经过点P（1，2）和点Q（0，3.5），用待定系数法即可得出此一次函数的解析式．

　　解答：设这个一次函数的解析式为y=kx+b．

　　           ∵这条直线经过点P（1，2）和点Q（0，3.5），

　　           ∴{ k+b=2    ①
　　               { b=3.5     ②

　　           解得{ k=-1.5
　　                  { b=3.5

　　           故这个一次函数的解析式为y=-1.5x+3.5，

　　           即：3x+2y-7=0．

　　           故选D．

________________________________________________________________________________________

　　例4：（2007·聊城）如图，以两条直线l1，l2的交点坐标为解的方程组是（　　）

                       

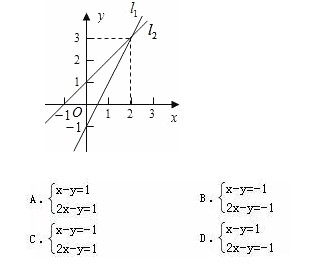
　　分析：两条直线的交点坐标应该是联立两个一次函数解析式所组方程组的解．因此本题需先根据两直线经过的点的坐标，用待定系数法求出两直线的解析式．然后联立两函数的解析式可得出所求的方程组．

　　解答：直线l1经过（2，3）、（0，-1），易知其函数解析式为y=2x-1；

　　           直线l2经过（2，3）、（0，1），易知其函数解析式为y=x+1；

　　           因此以两条直线l1，l2的交点坐标为解的方程组是： x-y=-1 2x-y=1   ．

　　           故选C．

________________________________________________________________________________________

　　例5：（2006·雅安）已知函数y=-2x+6与函数y=3x-4．

　　           （1）在同一平面直角坐标系内，画出这两个函数的图象；

　　           （2）求这两个函数图象的交点坐标；

　　           （3）根据图象回答，当x在什么范围内取值时，函数y=-2x+6的图象在函数y=3x-4的图象的上方？

　　分析：（1）可用两点法来画函数y=-2x+6与函数y=3x-4的图象；

　　           （2）两函数相交，那么交点的坐标就是方程组{ y=-2x+6，{ y=3x-4 的解；

　　           （3）函数y=-2x+6的图象在函数y=3x-4的图象的上方，即-2x+6＞3x-4，解得x＜2．

　　解答：（1）函数y=-2x+6与坐标轴的交点为（0，6），（3，0）

　　                   函数y=3x-4与坐标轴的交点为（0，-4），（4 3 ，0）

　　                  作图为：

                                

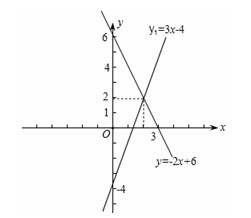
　　         （2）解：根据题意得

　　                方程组{ y=-2x+6   ①
　　                          { y=3x-4     ②

　　                解得 x=2， y=2

　　                即交点的坐标是（2，2）

　　               ∴两个函数图象的交点坐标为（2，2）

　　        （3）由图象知，当x＜2时，函数y=-2x+6的图象在函数y=3x-4的图象上方．

　　三、解题经验

　　理解两个函数图像交点处的各种意义，一般情况下，交点处表示两个函数的函数值相等。也表示这个两个同二元一次等方程组的解。交点往往是判断函数值大小的分界线。