圆中常用辅助线的添法

圆中常用辅助线的添法

                                         作者:会

圆是初中数学重点内容，属中考必考内容，中考中有关圆的问题，大部分需添辅助线解之，那么圆问题中常用的辅助线有哪些呢？现就圆中常用辅助线的添法作一归纳，以期对同学们的学习有所帮助．

一、             作弦心距.

在解决有关弦的问题时，常常作弦心距，以利用垂经定理或圆心角、弦、弦心距之间的关系定理及推论.

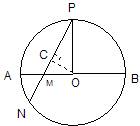例1.如图，ＡＢ是⊙O的直径,PO⊥AB交⊙O于P点，弦PN与AB相交于点M，

求证：PM·PN=2PO².

分析：要证明PM·PN=2PO²，即证明PM·PC =PO²，

过O点作OC⊥PN于C，根据垂经定理 NC=PC，只需证明

PM·PC=PO²，要证明PM·PC=PO²只需证明Rt△POC∽Rt△PMO.

证明: 过圆心O作OC⊥PN于C，∴PC= PN

∵PO⊥AB, OC⊥PN，∴∠MOP=∠OCP=90°.

又∵∠OPC=∠MPO，∴Rt△POC∽Rt△PMO.

∴ 即∴PO²= PM·PC.  ∴PO²= PM·PN，∴PM·PN=2PO².

二、             作直径所对的圆周角

在解决有关直径的问题时，常常作直径所对的圆周角，以利用直径所对的圆周角是直角的性质。

例2  如图，在△ABC中，∠C=90°，以BC上一点O为圆心，以OB为半径的圆交AB于点M，交BC于点N．

（1）       求证：BA·BM=BC·BN；

（2）       如果CM是⊙O的切线，N为OC的中点，当AC=3时，求AB的值．

分析：要证BA·BM=BC·BN，需证△ACB∽△NMB，而∠C=90°，所以需要△NMB中有个直角，而BN是圆O的直径，所以连结MN可得∠BMN=90°。

（1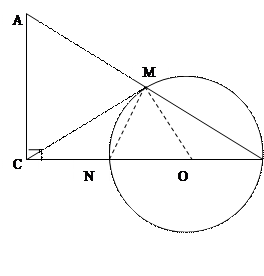）       证明：连结MN，则∠BMN=90°=∠ACB

∴△ACB∽△NMB

∴

∴AB·BM=BC·BN

（2）       解：连结OM，则∠OMC=90°

∵N为OC中点

∵OM=OB，∴∠B=∠MON=30°

∵∠ACB=90°，∴AB=2AC=2×3=6

三、连结半径

圆的半径是圆的重要元素，圆中的许多性质如：“同圆的半径相等”和“圆的切线垂直于过切点的半径”等都与圆的半径有关，连结半径是常用的方法之一.

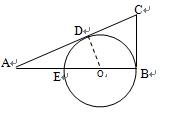例3．已知：如图，△ABC中，∠B=90°，O是AB上一点，以O为圆心，以OB为半径的圆切AC于D点，交AB与E点，AD=2，AE=1.

求CD的长.

分析：D为切点，连结DO，则∠ODA=90°.根据切线长定理，有CD=CB.DO=EO=半径r，在Rt△ADO中根据勾股定理或Rt△ADO~ Rt△ABC，即可求出CD.

证明: 连结DO  ∴OD⊥AC于D, ∴∠ODA =90°.

    ∵AB过O点, ∠B=90°. ∴BC为⊙O的切线, ∴CD=CB

设CD=CB=x,DO=EO=y

在Rt△ADO中，AO² =AD²+ DO²，AD=2，AE=1

∴, 解得 y=

在Rt△ABC中，AC² =AB²+ BC²，即(2+x)²=(1+ y + y)²+x², ∴x=3   ∴CD=3.

四、连结公共弦

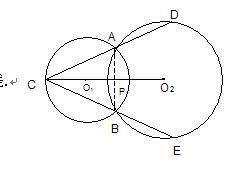在处理有关两圆相交的问题时，公共弦像一把“钥匙”，常常可以打开相应的“锁”，因此“遇到相交圆，连接公共弦.”。

例4．已知：如图，⊙O₁和⊙O₂相交于点A和B，

O₂O₁的延长线交⊙O₁于点C，CA、CB的延长线分                        

别和⊙O₂相交于点D、E，求证：AD=BE.  

 分析：⊙O₁和⊙O₂是相交的两圆，作公共弦AB为辅助线.

证明：连结AB交O₂O₁于P点 ，

∵O₁ O₂⊥A B且O₁O₂平分AB     ∴CA=CB

∴∠ACP=∠BCP     ∴点O₂到线段AD、BE的距离相等   ∴AD=BE.

 五、作连心线

    两圆相交，连心线垂直平分两圆的公共弦；两圆相切，连心线必过切点.通过作两圆的连心线，可沟通圆心距、公共弦、两圆半径之间的关系.因此，“已知有两圆，常画连心线.”.

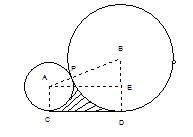例5．已知：如图，⊙A和⊙B外切于P点，⊙A的半径为r，⊙B的半径为3r, CD为⊙A、⊙B的外公切线，C、D为切点，求：（1）CD的长；（2）CD与弧PD及弧PC所围成的阴影部分的面积.

解：（1）连结AB、AC、BD

∵⊙A和⊙B外切于P点，∴AB过P点

∵CD为⊙A、⊙B的外公切线，C、D为切点，

∴AC⊥CD，BD⊥CD

过A点作AE⊥BD于E，则四边形ACDE为矩形.

∴DE=AC= r，BE=BD-DE=3r-r=2r

在Rt△AEB中，AB=AP+PB=r+3r=4r，BE=2r

∴AE=   ∴CD=2r  .

（2）由（1）可知COSB= ，∴∠B=60°.  ∴∠CAB=∠CAE+∠BAE=90°+30°=120°.

∴S_阴影=S梯形_ABDC-S扇形_BPD-S扇形_ACP

=4－π－ π=（4－π）

六、作公切线

分析：相切两圆过切点有一条公切线，这条公切线在解题时起着非常重要的作用，如下题中所作的内公切线MN起到沟通两圆的作用.因此，相切两圆过切点的公切线是常用辅助线.

例6．已知：⊙O₁和⊙O₂外切于点A，ＢＣ是⊙O₁和⊙O₂的外公切线，Ｂ、Ｃ为切点.

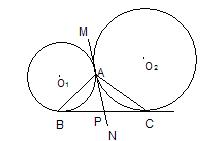求证：ＡＢ⊥AＣ

证明：过切点Ａ作公切线ＭＮ交ＢＣ于Ｐ点，

∵ＢＣ是⊙O₁和⊙O₂的外公切线，

∴ＰＢ＝ＰＡ＝ＰＣ

∴∠PBA=∠PAB，∠PAC=∠PCA

∵∠PBA+∠PAB+∠PAC+∠PCA= 180 °.

∴∠BAC= 90 °.

∴ＡＢ⊥AＣ.

七、切线判定分两种：公共点未知作垂线、公共点已知作半径

切线的判定定理是：“经过半径的外端,并且垂直于这条半径的直线是圆的切线.”，就是说，要判定一条直线是否是切线，应同时满足这样的两条：（1）直线经过半径的外端，（2）直线垂直于这条半径，所以,在证明直线是切线时, 往往需要通过作恰当的辅助线,才能顺利地解决问题.下面是添辅助线的小规律.

1．无点作垂线

需证明的切线，条件中未告之与圆有交点，则联想切线的定义，过圆心作该直线的垂线，证明垂足到圆心的距离等于半径.

例7．已知：如图，AB是⊙O的直径，AD⊥AB于A， BC⊥AB于B，若∠DOC= 90°.

求证：DC是⊙O的切线.

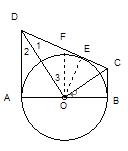分析：DC与⊙O没有交点，“无点作垂线”，过圆心O作OE⊥DC，只需证OE等于圆的半径.因为AO为半径，若能证OE=OA即可.而OE、OA在△DEO、△DAO中，需证明△DEO≌△DAO

证明：作OE⊥DC于E点，取DC的中点F，连结OF.

又∵∠DOC= 90°.  ∴ FO=FD  ∴∠1=∠3.

∵AD⊥AB，BC⊥AB,  ∴BC∥AD, ∴OF为梯形的中位线.

∴OF∥AD . ∴  ∠2=∠3.  ∴∠1=∠2.

∴DO是∠ADE的角平分线.  ∵OA⊥DA，OE⊥DC，

∴OA=OE=圆的半径.  ∴ DC是⊙O的切线.

2．有点连圆心.

当直线和圆的公共点已知时，联想切线的判定定理，只要将该点与圆心连结，再证明该半径与直线垂直.

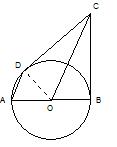例8．已知：如图，AB为⊙O的直径，BC为⊙O的切线，切点为B，OC平行于弦AD，求证：CD是⊙O的切线.

分析：D在⊙O上，有点连圆心，连结DO，证明DO⊥DC即可. 

证明：连结DO，∵OC∥AD    ∴∠DAO=∠COB，∠ADO=∠DOC

而∠DAO=∠ADO∴∠DOC=∠COB，又OC=OC，DO=BO ∴△DOC≌△BOC 

∴∠ODC=∠OBC， ∵BC为⊙O的切线，切点为B

∴∠OBC=90°， ∴∠ODC=90°，又D在⊙O上，

∴CD是⊙O的切线.

我们可以把圆中常用辅助线的规律总结为如下歌诀：

弦与弦心距，密切紧相连；直径对直角，圆心作半径；已知有两圆，常画连心线；.   

遇到相交圆，连接公共弦；遇到相切圆，作条公切线；“有点连圆心，无点作垂线.”

切线证明法，规律记心间.