数学破题36计第26计 数列开门 前后跟踪

第26计 数列开门 前后跟踪

●计名释义?

数列是特殊的函数，告诉了自变量是正自然数的函数，因此只要我们应知道这个特殊函数有两种关系式，除通项公式外，还有前后跟踪关系的递推式.高考30年来，数列的难题几乎都出现在递推式中.??

●典例示范?

【例1】   若数列{a_n}满足：a₁=1，a_n=+n+a_n-1， n∈N^*，n≥2，求证：a_n=，n∈N^*.?

【证明】   在递推式中，分别令n=2，3，4,…，直到n，得到(n-1)个等式：?

a₂=+2+a₁?                            a₃=+3+a₂?

a₄=+4+a₃……?                       a_n=??

将这(n-1)个等式整体相加得?

a_n=++…++2+3+…+n+a₁

=.

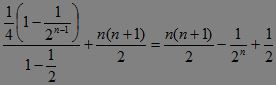当n=1时，a₁=1,也适合上式，?

∴a_n=，n∈N^*

【点评】   这里a_n与a_n-1的系数相等（都是1），并且在等号的两旁，因此由递推式得到的（n-1）个等式相加后，很多项可以消去，进而顺利求出a_n.?

由于数列可以看作是正整数n的函数，因此对于以递推关系式出现的问题，常常可以从递推关系式中的n=1，2，3，……入手，得到一系列的等式，通过对它们进行或加、或减、或乘、或除等运算，使问题获得解决.递推意识是解数列问题的一种最基本、最重要的意识.?

【例2】   (2006年全国卷Ⅰ)设数列{a_n}的前n项的和S_n=a_n-×2ⁿ⁺¹+,?n=1，2，3,……?（Ⅰ）求首项a₁与通项a_n；?

（Ⅱ）设T_n=，n=1，2，3,……求证：??

【解答】   （Ⅰ）a₁=S₁=a₁-，解得a=2.?

a_n+1=S_n+1-S_n=a_n+1-a_n-(2ⁿ⁺²-2ⁿ⁺¹),?∴a_n+1=4a_n+2ⁿ⁺¹?.?

这里a_n的系数是4，无法仿照例1直接用递推法求解.先将已知递推式的两边同除以2ⁿ⁺¹?得到?

若令b_n=，则有b_n+1=2b_n+1               (*)?

(*)式就是我们熟知的线性递推式，它可以运用待定系数法求解.?

设b_n+1+k=2(b_n+k)，即b_n+1=2b_n+k.?        ∴k=1，故=2(n∈N^*)，?

即{b_n+1}是以b₁+1为首项，2为公比的等比数列.?

∴b_n+1=(b₁+1)·2^n-1b_n=2ⁿ-1a_n=4ⁿ-2ⁿ.(n∈N*)?

（Ⅱ）S_n=a_n-×2ⁿ⁺¹ +=(4ⁿ-2ⁿ)- ×2ⁿ⁺¹ +=(2ⁿ⁺¹?-1)(2ⁿ-1).?

T_n=,?

∴?

【点评】   这里的递推式a_n+1=4a_n+2ⁿ⁺¹?化成b_n+1=2b_n+1后，形如a_n+1=Aa_n+B.?

对于a_n+1=Aa_n+B：当A=1时，a_n+1=a_n+B，?     即a_n+1-a_n=B，故通项a_n=a₁+(n-1)B；

?当A≠1时，a_n+1+k=Aa_n+B+k=A,?

令k=，则(A-1)k=B，即k=,?

∴{a_n+k}是以a₁+k=a₁+为首项，公比为A的等比数列.?

于是a_n+k=·A^n-1?，∴a_n=·A^n-1 -.??

【例3】   (2006年安徽高考题)数列{a_n}的前n项和为S_n，已知a₁=，S_n=n²aⁿ-n(n-1)，n=1,2,……写出S_n与S_n-1?的递推关系式(n≥2)，并求S_n关于n的表达式.?

【解答】   当n≥2时，a_n=S_n-S_n-1?,代入S_n=n²a_n-n(n-1)中，?

得S_n=n²(S_n-S_n-1?)-n (n-1),?       即(n²-1)S_n-n²S_n-1=n(n-1)               (*)?

这就是S_n与S_n-1?的递推关系式.?

将(*)式两边同除以n(n-1)得S_n-S_n-1=1(n≥2).?

构造新数列，它是以2S₁=2a₁=1为首项，1为公差的等差数列.?

于是=1+(n-1)×1=n，即S_n=(n≥2).?

显然，上式当n=1时也成立.∴S_n=，n∈N*.?

【点评】   这里构造新数列，关键在于能将（*）式变形为S_n-S_n-1=1,由此发现递推关系.?

高考中许多数列问题，往往是以等比、等差这两类基本数列为背景设计而成的.解决这类问题，常常可以通过构造新数列来实现问题的转化.强化构造意识，有助于创新能力的提高

●对应训练

1.假定一对刚出生的小兔一个月后能长成大兔，再过一个月便能生下一对小兔，并此后每一个月生一对小兔，如果不发生死亡，问一对刚出生的小兔一年可繁殖成多少对？?

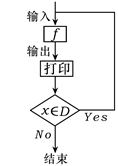2.对任意函数f (x)，x∈D,可按图所示构造

一个数列发生器，其工作原理如下：?

①       输入数据x₀∈D，经数列发生器

输出x₁=f (x₀);?

②若x₁D，则数列发生器结束工作；

若x₁∈D，则将x₁反馈回输入端，

再输出x₂=f(x₁)，并依此规律继续下去，

现定义f (x)=?

(1)    若输入x₀=则由数列发生器产生数列{x_n},           第2题图

请写出数列{x_n}的所有项；?

(2)若要数列发生器产生一个无穷常数数列，试求输入的初始数据x₀的值；?

(3)若输入x₀时，产生无穷数列{x_n}满足：对任意正整数n，均有x_n<x_n+1?，求x₀的取值范围.?

3.某公司全年的纯利润为b元，其中一部分作为奖金发给n位职工，奖金分配方案如下：首先将职工按工作业绩(工作业绩均不相同)从大到小，由1至n排序，第1位职工得奖金元，然后再将余额除以n发给第2位

职工，按此方法将奖金逐一发给每位职工，并将最后剩余部分作为公司发展基金.?

(1)设a_k(1≤k≤n)为第k位职工所得奖金额，试求a₂、a₃,并用k、n和b表示a_k;(不必证明)

(2)证明a_k>a_k+1?(k=1,2,…,n-1)，并解释此不等式关于分配原则的实际意义.?

(3)发展基金与n和b有关，记为P_n(b)，对常数b，当n变化时，求.

●参考答案?

1.把第n个月的兔子总数记为f (n)，则f (1)=1，f (2)=1，f (3)=2，f (4)=3，f (5)=5，f (6)=8，f (7)=13,…….考查数列{f (n)}的规律，不难发现，从第三项开始，第一项都是前两项之和：f (3)= f (1)+f (2)；f (4)= f (2)+f (3)；f (5)=f (3)+f (4)；f (6)= f (4)+f (5)；f (7)=f (5)+f (6);…，

f (13)= f (11)+f(12)=89+144=233,所以，一对兔子一年可繁殖成233对.?

2.(1)∵   f (x)的定义域D=(-∞,-1)∪(-1,+∞)?

∴   数列{x_n}只有三项：x₁=，x₂=，x₃=-1.?

(2)∵   f (x)==x即x²-3x+2=0,?                  ∴   x=1或x=2.?

即当x₀=1或2时，x_n+1==x_n?

故当x₀=1时，x_n=1；当x₀=2时，x_n=2(n∈N)?

(2)    解不等式x<,?

∴   <0，得x<-1或1<x<2，?

要使x₁<x₂，则x₁<-1或1<x₁<2,?

对于函数f (x)= =,?        若x₁<-1，则x₂=f (x₁)>4，x₃= f (x₂)<x₂,?

当x₁∈(1,2)时，x₂= f (x₁)>x₁，且1<x₂<2.  依次类推，可得数列{x_n}的所有项均

满足x_n+1>x_n(n∈N₊).?

综上所述，x₁∈(1,2)时，由x₁= f (x₀),?得x₀∈(1,2).??

点评   本题主要考查函数的基本知识，数列的基本知识，解不等式的基本方法，以及综合运用知识的能力和判断推理能力.本题利用框图形式把函数、数列、不等式等知识点冶为一炉，形式新颖，结构巧妙，富于思考.今后仍有可能出现这种富有创新意识的试题.?

3.(1)第1位职工的奖金a₁=；?第2位职工的奖金a₂=；

?第3位职工的奖金a₃=；……?第k位职工的奖金a_k=.??

(2)a_k  - a_k+1=>0.

此奖金分配方案体现了“按劳分配”或“不吃大锅饭”等原则.?

（3）设f_k(b)表示奖金发给第k位职工后所剩余款，则

?f₁(b)=，f₂(b)=，…，f_k(b)=.?

得   P_n(b)= f_n(b)=，?               故   .?

点评：本题主要考查数列、不等式、极限的综合运用以及结合职

工福利的实际应用，这正是近年高考命题的热点和重点.??