初中数学：用整体思想解分式题

例1、计算：

分析：将每个分母看作一个整体，则从每个分式中可以拆出“1”。

解：原式

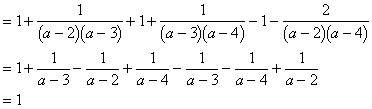
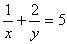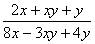例2、已知，求代数式的值。

分析：由条件可得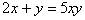，而待求式也含有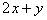与xy的式子，所以可将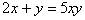整体代入。

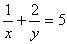解：由，得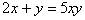

所以原式

例3、已知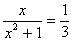，则___________。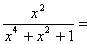

分析：取已知式和待求式的倒数。

观察已知式和待求式，它们的分子都是单项式，而分母都是多项式，若整体倒换后就可逆用分式加减法的运算法则，得出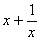的式子，再把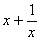作为整体代入求值。

解：由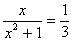，得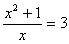

即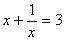

所以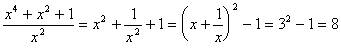

故原式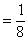

例4、A、B、C、D、E五人合做一项工程，已知A、B、C合作7.5小时可以完成；A、C、E合作5小时可以完成；A、C、D合作6小时可以完成；B、D、E合作4小时可以完成，问五人合做需几小时完成？

分析：设A、B、C、D、E各自独立完成此项工程所需时间分别是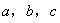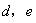，小时，根据题意，得

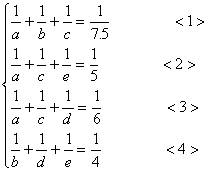
常规方法是先求出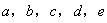的值，然后代入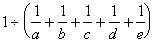，从而得出答案，但由于上述方程组是不定方程组，因而不可能求得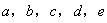的值。这时若注意到本题是求5人合作完成此项工程的时间，实际上只要能求出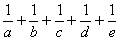即可，因而可把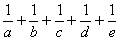视为整体，直接求出。

将四式相加，得

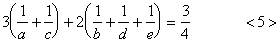
把<4>代入<5>，得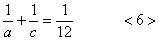  

<4>＋<6>，得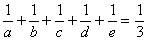  

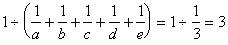
故五人合作完成此项工程需3小时。