二次函数典型题(三)代几综合
已知抛物线的顶点为(3, -2), 且在x轴上截得的线段AB长为4.
(1) 求这个抛物线的解析式;
(2) 抛物线上是否存在点Q, 使△QAB面积等于12? 如果存在, 请求出点Q的坐标; 如果不存在, 请说明理由.
【解析】 (1)抛物线解析式的求法是常考知识点, 虽然不同的题目给出的条件不一样, 但是解题的思想比较少, 一般用待定系数法都可以解决.
∵题目中给出了抛物线的顶点,
∴我们设抛物线的顶点式: y=a(x-3)2-2.
接下来的任务是再找一个点.
∵抛物线的顶点为(3, -2), ∴当函数图像在x轴上截得的线段AB长为4时, 我们可以知点A、 B到x=3的距离都为2, 则A、 B的坐标分别为: (1,0)和(5,0).
把x=1, y=0代入y=a(x-3)2-2得
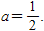
∴抛物线的解析式为
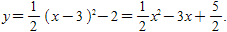
(2) 这小题重点考察了数形结合的思想和观察能力.
这小题不画图, 靠空想是很难想出来的, 只要先把二次函数的图象画出来, 通过观察和分析图象的特点帮助解决问题.
二次函数的图象如下:
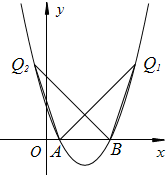
从图象上观察, 发现可能存在两个这样的点. 现在我们假设存在点Q, 并时高点Q的坐标为(a,b). 下一步我们只要能够求出a、 b的具体值, 就可以说明点Q的存在.
要求出这两个未知数, 我们就要找到等量关系, 列出方程. 而这个等量关系就是: △QAB面积等于12.
∵S△QAB=(1)/(2)AB·|b|=2|b|=12,

∴点Q的坐标为(7,6) 或(-1,6).
即存在这样的点Q.
相关文章
- 三角函数只会考这些题,你掌握了吗?
- 《二次函数》知识点梳理与学习建议
- 面积求法大全——中考压轴题分析
- 二次函数—考点二
- 秒杀一元二次函数值域问题
- 大赞!老师连夜整理的函数解题技巧,一看就懂!人手一份!
- 函数值域求法十五种
- 中考专题复习——函数
- 初中函数不过关,想得高分肯定难!掌握两个“诀窍”,为孩子排
- 孩子的“函数问题”还没有弄明白?掌握这些小技巧中考轻松涨10
- 据说90%的初中生都死在了这道题上,快来看看你会不会做
- 这四张图把初中二次函数总结了起来,建议家长给孩子看看!
- 初三 | “二次函数”知识点总结,附10个经典题型!
- 破解中考之坐标几何题——坐标平面中的函数问题
- 一次函数,常考7种形式!(附例)
- 让你彻底弄懂“函数”——轻松破解中考压轴题
- 函数及其图象:函数与平面直角坐标系考点全透析(初二快,初三
- 【知识点】函数(数与形的结合)
- 三角函数最值问题的解题规律
- “7分钟学完3年函数,中考只考5点!”初中老师“一语惊人”
推荐内容
教育新鲜事
 上课老走神怎么办?9张
上课老走神怎么办?9张 中考过来人传授经验
中考过来人传授经验 谁把初中各科答题套路编
谁把初中各科答题套路编 衡水中学关于考试的51条
衡水中学关于考试的51条