立体几何中的轨迹问题
以立体图形为载体的轨迹问题,将立体几何和解析几何巧妙地整合在一起。解答这类问题的关键是把空间问题转化为平面问题,一般可从两个方面考虑:一是利用曲线的定义,二是用解析法求出轨迹方程。
例1、已知平面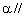 平面
平面 ,直线
,直线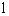
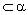 ,点
,点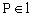 ,平面
,平面 、
、 间的距离为4,则在
间的距离为4,则在 内到点P的距离为5且到直线
内到点P的距离为5且到直线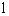 的距离为
的距离为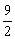 的点的轨迹是( )
的点的轨迹是( )
A. 一个圆
B. 两条平行直线
C. 四个点
D. 两个点
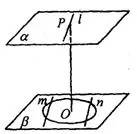
图1
简析:如图1,设点P在平面 内的射影是O,则OP是
内的射影是O,则OP是 、
、 的公垂线,OP=4。在
的公垂线,OP=4。在 内到点P的距离等于5的点到O的距离等于3,可知所求点的轨迹是
内到点P的距离等于5的点到O的距离等于3,可知所求点的轨迹是 内在以O为圆心,3为半径的圆上。又在
内在以O为圆心,3为半径的圆上。又在 内到直线
内到直线 的距离等于
的距离等于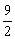 的点的集合是两条平行直线m、n,它们到点O的距离都等于
的点的集合是两条平行直线m、n,它们到点O的距离都等于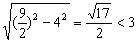 ,所以直线m、n与这个圆均相交,共有四个交点。因此所求点的轨迹是四个点,故选C。
,所以直线m、n与这个圆均相交,共有四个交点。因此所求点的轨迹是四个点,故选C。
总结:本题以空间直线与平面的位置关系为依据,研究平面解析几何的点的轨迹问题。
例2、在四棱锥 中,
中, 面PAB,
面PAB,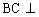 面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,
面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,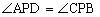 ,满足上述条件的四棱锥的顶点P的轨迹是( )
,满足上述条件的四棱锥的顶点P的轨迹是( )
A. 圆
B. 不完整的圆
C. 抛物线
D. 抛物线的一部分
简析:因为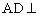 面PAB,
面PAB,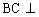 面PAB,所以AD//BC,且
面PAB,所以AD//BC,且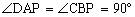 。
。
又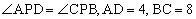 ,
,
可得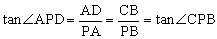 ,
,
即得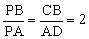
在平面PAB内,以AB所在直线为x轴,AB中点O为坐标原点,建立平面直角坐标系,则A(-3,0)、B(3,0)。设点P(x,y),则有
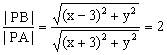 ,
,
整理得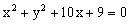
由于点P不在直线AB上,故此轨迹为一个不完整的圆,选B。
总结:根据题目的信息,利用空间几何性质,把立体几何问题转化到平面上,再利用解析几何的方法探求轨迹。
例3、如图2,定点A和B都在平面 内,定点P
内,定点P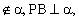 C是
C是 内异于A和B的动点。且
内异于A和B的动点。且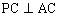 ,那么动点C在平面
,那么动点C在平面 内的轨迹是( )
内的轨迹是( )
A. 一条线段,但要去掉两个点
B. 一个圆,但要去掉两个点
C. 一个椭圆,但要去掉两个点
D. 半圆,但要去掉两个点
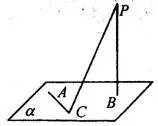
图2
简析:因为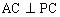 ,且PC在
,且PC在 内的射影为BC,所以
内的射影为BC,所以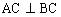 ,即
,即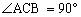 。所以点C的轨迹是以AB为直径的圆且去掉A、B两点,故选B。
。所以点C的轨迹是以AB为直径的圆且去掉A、B两点,故选B。
总结:本题主要考查圆、线面垂直的基本知识,利用线面垂直的条件,将空间问题转化到平面上的圆的问题。
例4、如图3,在正方体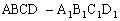 中,P是侧面
中,P是侧面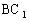 内一动点,若P到直线BC与直线
内一动点,若P到直线BC与直线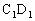 的距离相等,则动点P的轨迹所在的曲线是( )
的距离相等,则动点P的轨迹所在的曲线是( )
A. 直线 B. 圆 C. 双曲线 D. 抛物线
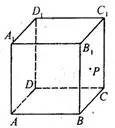
图3
简析:因为P到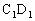 的距离即为P到
的距离即为P到 的距离,所以在面
的距离,所以在面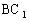 内,P到定点
内,P到定点 的距离与P到定直线BC的距离相等。由圆锥曲线的定义知动点P的轨迹为抛物线,故选D。
的距离与P到定直线BC的距离相等。由圆锥曲线的定义知动点P的轨迹为抛物线,故选D。
总结:本题以立体几何知识为载体,考查了圆锥曲线的概念等基础知识,将抛物线的动态定义寓于正方体之中。
例5、已知正方体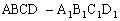 的棱长为1,点P是平面AC内的动点,若点P到直线
的棱长为1,点P是平面AC内的动点,若点P到直线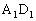 的距离等于点P到直线CD的距离,则动点P的轨迹所在的曲线是( )
的距离等于点P到直线CD的距离,则动点P的轨迹所在的曲线是( )
A. 抛物线
B. 双曲线
C. 椭圆
D. 直线
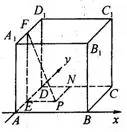
图4
简析:如图4,以A为原点,AB为x轴、AD为y轴,建立平面直角坐标系。设P(x,y),作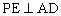 于E、
于E、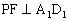 于F,连结EF,易知
于F,连结EF,易知
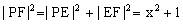
又作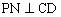 于N,则
于N,则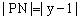 。
。
依题意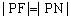 ,
,
即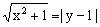 ,
,
化简得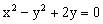
故动点P的轨迹为双曲线,选B。
例6、已知异面直线a,b成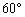 角,公垂线段MN的长等于2,线段AB两个端点A、B分别在a,b上移动,且线段AB长等于4,求线段AB中点的轨迹方程。
角,公垂线段MN的长等于2,线段AB两个端点A、B分别在a,b上移动,且线段AB长等于4,求线段AB中点的轨迹方程。
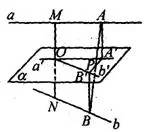
图5
简析:如图5,易知线段AB的中点P在公垂线段MN的中垂面 上,直线
上,直线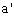 、
、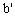 为平面
为平面 内过MN的中点O分别平行于a、b的直线,
内过MN的中点O分别平行于a、b的直线,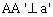 于
于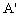 ,
,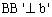 于
于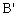 ,则
,则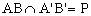 ,且P也为
,且P也为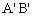 的中点。
的中点。
由已知MN=2,AB=4,易知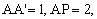 得
得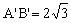 。
。
则问题转化为求长等于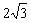 的线段
的线段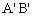 的两个端点
的两个端点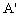 、
、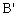 分别在
分别在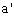 、
、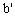 上移动时其中点P的轨迹。现以
上移动时其中点P的轨迹。现以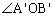 的角平分线为x轴,O为原点建立如图6所示的平面直角坐标系。
的角平分线为x轴,O为原点建立如图6所示的平面直角坐标系。
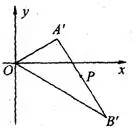
图6
设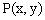 ,
,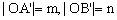 ,
,
则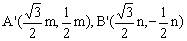
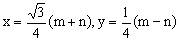
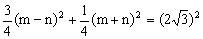
消去m、n,得线段AB的中点P的轨迹为椭圆,其方程为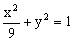 。
。
总结:例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起。
推荐内容
教育新鲜事
 高中丨(高频考点)物理
高中丨(高频考点)物理 期末考试时间定了!收官
期末考试时间定了!收官 高中生逆袭物语:这几步
高中生逆袭物语:这几步 必须收藏!省略句考点全
必须收藏!省略句考点全