高中数学典型例题解析(第十章导数及其应用2)
三、经典例题导讲
[例1]已知曲线![]() 及点
及点![]() ,求过点
,求过点![]() 的曲线
的曲线![]() 的切线方程.
的切线方程.
错解:![]() ,
,![]() 过点
过点![]() 的切线斜率
的切线斜率![]() ,
,![]() 过点
过点![]() 的曲线
的曲线![]() 的切线方程为
的切线方程为![]() .
.
错因:曲线在某点处的切线斜率是该曲线对应的函数在该点处的导数值,这是导数的几何意义.在此题中,点![]() 凑巧在曲线
凑巧在曲线![]() 上,求过点
上,求过点![]() 的切线方程,却并非说切点就是点
的切线方程,却并非说切点就是点![]() ,上述解法对求过点
,上述解法对求过点![]() 的切线方程和求曲线在点
的切线方程和求曲线在点![]() 处的切线方程,认识不到位,发生了混淆.
处的切线方程,认识不到位,发生了混淆.
正解:设过点![]() 的切线与曲线
的切线与曲线![]() 切于点
切于点![]() ,则过点
,则过点![]() 的曲线
的曲线![]() 的切线斜率
的切线斜率
![]() ,又
,又![]() ,
,![]() 。①
。①![]() 点
点![]() 在曲线
在曲线![]() 上,
上,
![]() ②,②代入①得
②,②代入①得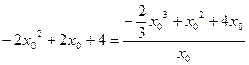
化简,得![]() ,
,![]() 或
或![]() .若
.若![]() ,则
,则![]() ,过点
,过点![]() 的切线方程为
的切线方程为![]() ;若
;若![]() ,则
,则![]() ,过点
,过点![]() 的切线方程为
的切线方程为![]()
![]() 过点
过点![]() 的曲线
的曲线![]() 的切线方程为
的切线方程为![]() 或
或![]()
[例2]已知函数![]() 在
在![]() 上是减函数,求
上是减函数,求![]() 的取值范围.
的取值范围.
错解:![]()
![]()
![]() 在
在![]() 上是减函数,
上是减函数,![]() 在
在![]() 上恒成立,
上恒成立,
![]() 对一切
对一切![]() 恒成立,
恒成立,![]() ,即
,即![]() ,
,![]() .
.
正解:![]()
![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,![]()
![]()
![]() 在
在![]() 上恒成立,
上恒成立,![]() 且
且![]() ,即
,即![]() 且
且![]() ,
,![]() .
.
[例3]当 ![]() ,证明不等式
,证明不等式![]() .
.
证明:![]() ,
,![]() ,则
,则![]() ,当
,当![]() 时。
时。![]() 在
在![]() 内是增函数,
内是增函数,![]() ,即
,即![]() ,又
,又![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 内是减函数,
内是减函数,![]() ,即
,即![]() ,因此,当
,因此,当![]() 时,不等式
时,不等式![]() 成立.
成立.
点评:由题意构造出两个函数![]() ,
,![]() .利用导数求函数的单调区间,从而导出
.利用导数求函数的单调区间,从而导出![]() 及
及![]() 是解决本题的关键.
是解决本题的关键.
[例4]设工厂到铁路线的垂直距离为20km,垂足为B.铁路线上距离B为100km处有一原料供应站C,现要在铁路BC之间某处D修建一个原料中转车站,再由车站D向工厂修一条公路.如果已知每千米的铁路运费与公路运费之比为3:5,那么,D应选在何处,才能使原料供应站C运货到工厂A所需运费最省?
解 : 设BD之间的距离为![]() km,则|AD|=
km,则|AD|=![]() ,|CD|=
,|CD|=![]() .如果公路运费为
.如果公路运费为![]() 元/km,那么铁路运费为
元/km,那么铁路运费为![]() 元/km.故从原料供应站C途经中转站D到工厂A所需总运费
元/km.故从原料供应站C途经中转站D到工厂A所需总运费![]() 为:
为:![]()
![]() +
+![]()
![]() ,(
,(![]() ).对该式求导,得
).对该式求导,得![]() =
=![]() +
+![]() =
=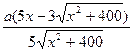 ,令
,令![]() ,即得25
,即得25![]() =9(
=9(![]()
![]() ),解之得
),解之得
![]() =15,
=15,![]() =-15(不符合实际意义,舍去).且
=-15(不符合实际意义,舍去).且![]() =15是函数
=15是函数![]() 在定义域内的唯一驻点,所以
在定义域内的唯一驻点,所以![]() =15是函数
=15是函数![]() 的极小值点,而且也是函数
的极小值点,而且也是函数![]() 的最小值点.由此可知,车站D建于B,C之间并且与B相距15km处时,运费最省.
的最小值点.由此可知,车站D建于B,C之间并且与B相距15km处时,运费最省.
点评: 这是一道实际生活中的优化问题,建立的目标函数是一个复合函数,用过去的知识求其最值往往没有一般方法,即使能求出,也要涉及到较高的技能技巧.而运用导数知识,求复合函数的最值就变得非常简单.一般情况下,对于实际生活中的优化问题,如果其目标函数为高次多项式函数、简单的分式函数简单的无理函数、简单的指数、对数函数,或它们的复合函数,均可用导数法求其最值.由此也可见,导数的引入,大大拓宽了中学数学知识在实际优化问题中的应用空间.
[例5]函数![]() ,其中
,其中![]() 是
是![]() 的导函数.(1)对满足-1≤
的导函数.(1)对满足-1≤![]() ≤1的一切
≤1的一切![]() 的值,都有
的值,都有![]() <0,求实数
<0,求实数![]() 的取值范围;
的取值范围;
(2)设![]() =-
=-![]() ,当实数
,当实数![]() 在什么范围内变化时,函数
在什么范围内变化时,函数![]() =
=![]() 的图象与直线
的图象与直线![]() =3只有一个公共点.
=3只有一个公共点.
解:(1)由题意![]()
令![]() ,
,![]()
对![]() ,恒有
,恒有![]() ,即
,即![]()
∴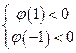 即
即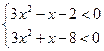
解得![]()
故![]() 时,对满足-1≤
时,对满足-1≤![]() ≤1的一切
≤1的一切![]() 的值,都有
的值,都有![]() .
.
(2)![]()
①当![]() 时,
时,![]() 的图象与直线
的图象与直线![]() 只有一个公共点
只有一个公共点
②当![]() 时,列表:
时,列表:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
极大
![]()
极小
![]()
∴![]()
又∵![]() 的值域是
的值域是![]() ,且在
,且在![]() 上单调递增
上单调递增
∴当![]() 时函数
时函数![]() 的图象与直线
的图象与直线![]() 只有一个公共点.
只有一个公共点.
当![]() 时,恒有
时,恒有![]()
由题意得![]()
即![]()
解得![]()
综上,![]() 的取值范围是
的取值范围是![]() .
.
[例6]若电灯B可在桌面上一点O的垂线上移动,桌面上有与点O距离为![]() 的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?(
的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?(![]() 照度与
照度与![]() 成正比,与
成正比,与![]() 成反比)
成反比)
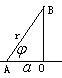 分析:如图,由光学知识,照度
分析:如图,由光学知识,照度![]() 与
与![]() 成正比,与
成正比,与![]() 成反比,
成反比,
即![]() (
(![]() 是与灯光强度有关的常数)要想点
是与灯光强度有关的常数)要想点![]() 处有最
处有最
大的照度,只需求![]() 的极值就可以了.
的极值就可以了.
解:设![]() 到
到![]() 的距离为
的距离为![]() ,则
,则![]() ,
,![]()
于是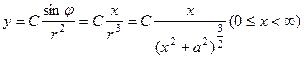 ,
, .
.
当![]() 时,即方程
时,即方程![]() 的根为
的根为![]() (舍)与
(舍)与![]() ,在我们讨论的半闭区间
,在我们讨论的半闭区间![]() 内,所以函数
内,所以函数![]() 在点
在点![]() 取极大值,也是最大值。即当电灯与
取极大值,也是最大值。即当电灯与![]() 点距离为
点距离为![]() 时,点
时,点![]() 的照度
的照度![]() 为最大.
为最大.
(0,![]() )
)
![]()
![]()
+
-
![]()
![]() ↗
↗
↘
点评:在有关极值应用的问题中,绝大多数在所讨论的区间上函数只有一点使得![]() =0且在该点两侧,
=0且在该点两侧,![]() 的符号各异,一般称为单峰问题,此时,该点就是极值点,也是最大(小)值点.
的符号各异,一般称为单峰问题,此时,该点就是极值点,也是最大(小)值点.
四、典型习题导练
1.已知函数![]() ,若
,若![]() 是
是![]() 的一个极值点,则
的一个极值点,则![]() 值为
( )
值为
( )
A.2
B.-2 C. ![]() D.4
D.4
2.已知函数![]() 在
在![]() 处有极值为10,则
处有极值为10,则![]() =
.
=
.
3.给出下列三对函数:①![]() ②
②![]() ,
,![]()
③![]() ,
,![]() ;其中有且只有一对函数“既互为反函数,又同是各自定义域上的递增函数”,则这样的两个函数的导函数分别是
;其中有且只有一对函数“既互为反函数,又同是各自定义域上的递增函数”,则这样的两个函数的导函数分别是![]() ,
,![]() .
.
4.已知函数![]() 有极大值和极小值,求
有极大值和极小值,求![]() 的取值范围.
的取值范围.
5.已知抛物线![]() ,过其上一点
,过其上一点![]() 引抛物线的切线
引抛物线的切线![]() ,使
,使![]() 与两坐标轴在第一象限围成的三角形的面积最小,求
与两坐标轴在第一象限围成的三角形的面积最小,求![]() 的方程.
的方程.
6.设![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,![]() ,
,
(1)求![]() 的表达式;(2)求
的表达式;(2)求![]() 的最大值.
的最大值.
§10.3定积分与微积分基本定理
一、知识导学
1.可微:若函数![]() 在
在![]() 的增量
的增量![]() 可以表示为
可以表示为![]() 的线性函数
的线性函数![]() (
(![]() 是常数)与较
是常数)与较![]() 高阶的无穷小量之和:
高阶的无穷小量之和:![]() (1),则称函数
(1),则称函数![]() 在点
在点![]() 可微,(1)中的
可微,(1)中的![]() 称为函数
称为函数![]() 在点
在点![]() 的微分,记作
的微分,记作![]() 或
或![]() .函数
.函数![]() 在点
在点![]() 可微的充要条件是函数
可微的充要条件是函数![]() 在
在![]() 可导,这时(1)式中的
可导,这时(1)式中的![]() 等于
等于![]() .若函数
.若函数![]() 在区间
在区间![]() 上每点都可微,则称
上每点都可微,则称![]() 为
为![]() 上的可微函数.函数
上的可微函数.函数![]() 在
在![]() 上的微分记作
上的微分记作![]() .
.
2.微积分基本定理:如果![]() ,且
,且![]() 在
在![]() 上可积.则
上可积.则
![]() .其中
.其中![]() 叫做
叫做![]() 的一个原函数.
的一个原函数.
由于![]() ,
,![]() 也是
也是![]() 的原函数,其中
的原函数,其中![]() 为常数.
为常数.
二、疑难知识导析
1 .定积分的定义过程包括“分割、近似求和、取极限”这几个步骤,这里包含着很重要的数学思想方法,只有对定积分的定义过程了解了,才能掌握定积分的应用.
1)一般情况下,对于区间的分割是任意的,只要求分割的小区间的长度的最大者![]() 趋近于0,这样所有的小区间的长度才能都趋近于0,但有的时候为了解题的方便,我们选择将区间等份成
趋近于0,这样所有的小区间的长度才能都趋近于0,但有的时候为了解题的方便,我们选择将区间等份成![]() 份,这样只要2其中的使
份,这样只要2其中的使![]() 就可以了.
就可以了.
2)对每个小区间内![]() 的选取也是任意的,在解题中也可选取区间的左端点或是右端点.
的选取也是任意的,在解题中也可选取区间的左端点或是右端点.
3)求极限的时候,不是![]() ,而是
,而是![]() .
.
2.在微积分基本定理中,原函数不是唯一的,但我们只要选取其中的一个就可以了,一般情况下选那个不带常数的。因为![]() .
.
3.利用定积分来求面积时,特别是位于![]() 轴两侧的图形的面积的计算,分两部分进行计算,然后求两部分的代数和.
轴两侧的图形的面积的计算,分两部分进行计算,然后求两部分的代数和.
三 、经典例题导讲
[例1]求曲线![]() 与
与![]() 轴在区间
轴在区间![]() 上所围成阴影部分的面积S.
上所围成阴影部分的面积S.
错解:分两部分,在![]()
![]() ,在
,在![]()
![]() ,因此所求面积
,因此所求面积![]() 为
2+(-2)=0。
为
2+(-2)=0。
分析:面积应为各部分积分的代数和,也就是第二部分的积分不是阴影部分的面积,而是面积的相反数。所以不应该将两部分直接相加。
正解:![]()
![]()
[例2]用微积分基本定理证明
![]() (
(![]() )
)
分析:即寻找![]() 的原函数代入进行运算。
的原函数代入进行运算。
解;设![]() ,则
,则![]()
=![]() =
=![]()
由微积分基本定理的逆运用可知:上式![]()
所以原式成立,即证。
注:该式可用来求分布在![]() 轴两侧的图形的积分。
轴两侧的图形的积分。
[例3]根据等式求常数![]() 的值。
的值。
1)![]() 2)
2)![]()
分析:利用微积分基本定理,求出原函数代入![]() 求解
求解
解:1)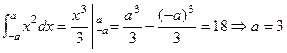
2)![]()
[例4]某产品生产x个单位时的边际收入![]()
(1) 求生产了50个单位时的总收入。
(2) 如果已生产了100个单位时,求再生产100个单位时的总收入。
分析:总收入为边际收入的积分和,求总收入既为求边际收入在规定时间内的定积分。由收入函数![]() 和边际收入
和边际收入![]() 的关系可得
的关系可得
(1)生产50个单位时的总收入为![]()
=![]() =99875
=99875
(2)已生产了100个单位时后,再生产100个单位时的总收入为![]()
答:生产50个单位时的总收入为99875;生产了100个单位时后,再生产100个单位时的总收入为19850.
[例5]一个带电量为![]() 的电荷放在
的电荷放在![]() 轴上原点处,形成电场,求单位正电荷在电场力作用下沿
轴上原点处,形成电场,求单位正电荷在电场力作用下沿![]() 轴方向从
轴方向从![]() 处移动到
处移动到![]() 处时电场力对它所作的功。
处时电场力对它所作的功。
分析:变力做功的问题就是定积分问题在物理方面的应用。
解:单位正电荷放在电场中,距原点![]() 处,电荷对它的作用力为
处,电荷对它的作用力为![]()
在单位电荷移动的过程中,电场对它的作用力为变力。则根据课本对变力做功的分析可知
![]()
答:电场力对它做的功为![]() 。
。
[例6]一质点以速度![]() 沿直线运动。求在时间间隔
沿直线运动。求在时间间隔![]() 上的位移。
上的位移。
分析:变速求位移和变力求功一样都可以用定积分解决。
解:![]()
![]()
答:位移为![]() 。
。
四、典型习题导练
1.![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() ( )
( )
A.0 B.2 C.-2 D.4
3.![]() ,则
,则![]() 。
。
4.利用概念求极限: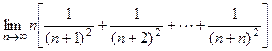
5.求下列定积分;
(1)![]() (2)
(2)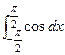
6.写出下面函数在给定区间上的总和![]() 及
及![]() 的表达式
的表达式
![]()
![]()
相关文章
- 高中数学“函数”必考知识点及常考题型总结
- 高考数学干货丨最容易出错的十道函数经典例题,快来巩固一下吧!
- 【高中数学】《三角函数》“诱导公式”大汇总
- 高中数学最容易出错的十道函数经典例题,快来巩固吧!
- 高中数学必修:三角函数知识点归纳,三角函数题型再不丢分!
- 高中数学压轴题系列之导数,构造函数解题法!转给孩子!
- 高中数学函数各种题型、快速解题技巧大全!可下载打印,手慢无!
- 高中数学三角函数知识点汇总!
- 高中数学关于函数的疑难问题,答案都在这里了!
- 高中数学全部函数图像与性质,赶紧收藏!
- 新高一,赢在起跑线!高中数学第五课,指数函数知识点汇总
- 高中数学老师教案:三角函数易丢分题型 6招拒绝再错!
- 高中数学:“导数”问题大集合,搞清这4点胜过刷100道题
- 2017年高考数学:导数压轴题7大题型归类总结,逆袭140
- 尖子班数学老师: 高中3年, 只考5个函数!
- 2017年高考数学必考热点高频考点,解题技巧都在这里
- 高一数学致胜微方法万能解题模版在函数求最值的应用
- 高一数学:三角函数与立体几何周测试卷
- 2017高考数学导数
- 2017年 高考数学又一高频考点,三招搞定
推荐内容
教育新鲜事
 高中数学“函数”必考知
高中数学“函数”必考知 高考数学答题方法的19条
高考数学答题方法的19条 高考数学干货丨最容易出
高考数学干货丨最容易出 【高中数学】《三角函数
【高中数学】《三角函数