――――――――――――――――

核心考点“函数的表示方法和分段函数”的【方法突破】

1、突破已知函数解析式求函数值的方法

【经典考题1】（1）(2012年高考福建卷)设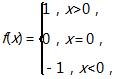







则f(g(π))的值为(　　)

A．1

B．0

C．－1

D．π

解析：∵g(π)＝0，∴f[g(π)]＝f(0)＝0，选B.

答案：B

（2）已知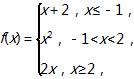若f(x)＝3，则x的值是(　　)

A．1

B．1或3/2

C．1，3/2或±√3

D.√3

解析：当x≤－1时，f(x)的值域为(－∞，1]；当－1<x<2时，f(x)的值域为[0,4]；当x≥2时，f(x)的值域为[4，＋∞)．而3∈[0,4)，所以f(x)＝x2＝3，所以x＝±√3，又因为－1<x<2，所以x＝√3

答案：D

2.突破函数解析式求法的方法

【经典考题2】(1)已知f(x+1/x）=x2+1/x2求f(x)的解析式；

(2)已知f(2/x+1)=lgx,求f(x)的解析式；

(3)已知f(x)是一次函数，且满足3f(x＋1)－2f(x－1)＝2x＋17，求f(x)的解析式；

(4)已知f(x)满足2f(x)＋f(1/x）=3x，求f(x)的解析式．

解析：(1)令x＋x/1＝t，则t2＝x2＋1/x2＋2≥4.

∴t≥2或∴f(t)＝t2－2，即f(x)＝x2－2(x≥2或x≤－2)．

(2)令2/x＋1＝t，由于x>0，

∴t>1且x＝2/（t－1)，

∴f(t)＝lg{2/(t－1)}，即f(x)＝lg{2/（x－1）}(x>1)．

(3)设f(x)＝kx＋b，

∴3f(x＋1)－2f(x－1)

＝3[k(x＋1)＋b]－2[k(x－1)＋b]

＝kx＋5k＋b＝2x＋17.

t≤－2且x2＋1/（x2）＝t2－2，

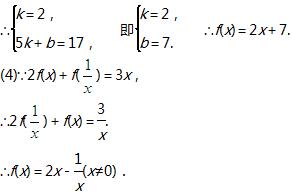揭示方法：

函数解析式的求法:

(1)凑配法，由已知条件f(g(x)）=F（x），可将F(x)改写成关于g（x）的表达式，然后以x替代g（x），得到f（x）的解析式;

(2)特定系数法：若已知函数的类型（如一次函数，二次函数），可用待定系数法。

(3)换元法：已知复合函数f（g（x））的解析式，可用换元法，此时要注意新元的取值范围。

(4)方程思想：已知关于f（x）与f（1/x）或f（-x）的表达式，可根据已知条件再构造出另外一个等式组成方程组，通过解方程组求出f（x）。

3突破求分段函数中的求参数问题。

【经典考题3】(江苏高考)已知实数a≠0，函数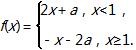



若f(1－a)＝f(1＋a)，则a的值为______．

解析：首先讨论1－a,1＋a与1的关系，当a<0时，1－a>1,1＋a<1，所以f(1－a)＝－(1－a)－2a＝－1－a；f(1＋a)＝2(1＋a)＋a＝3a＋2.

因为f(1－a)＝f(1＋a)，所以－1－a＝3a＋2，即a＝－3/4.

当a>0时，1－a<1,1＋a>1，所以f(1－a)＝2(1－a)＋a＝2－a；f(1＋a)＝－(1＋a)－2a＝－3a－1.

因为f(1－a)＝f(1＋a)，所以2－a＝－3a－1，所以a＝－3/2(舍去)．

综上，满足条件的a＝－3/4

【答案】　－3/4

揭示方法：分段函数求值的关键在于判断所给自变量的取值是否符合所给分段函数中的哪一段定义区间，要不明确则要分类讨论．