高一高二必读:三角恒等变换的“五大技巧”

三角恒等变换问题在历年高考和自主招生试题中屡见不鲜,主要考查考生的逻辑推理和运算求解能力。下面着重分析各类试题中有关三角恒等变换的问题,主要剖析命题的切入点以及围绕三角恒等变换的解题方法和思路。
一、化切为弦,关注通法
通过化切为弦、正余互化等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法。它实质上是化归的思想,通过化归与转化有利于问题的解决或发现解题途径。

本题是一道标准的“化切为弦”问题。本题还有一种变换方法如下:
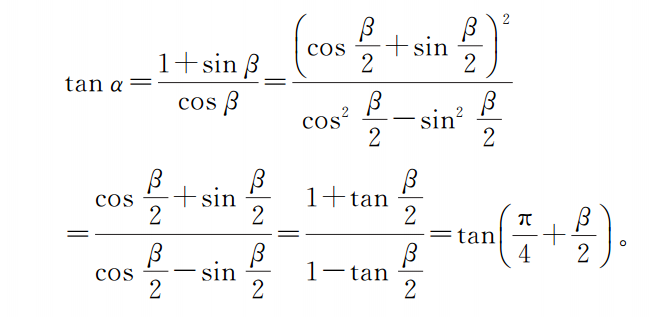
二、正难则反,公式逆用
按照常规的解题思路,大家习惯公式的正用,而不习惯“倒着想,反着用”。如果说公式的正用是拆分的过程,那么公式的逆用则是合并的过程。从思维上来讲,公式的逆用,体现了逆向思维,是一个配凑的过程,更体现了构造的思想,因此要求更高。
公式逆用中,考题常涉及辅助角公式。在用辅助角公式时经常会涉及三角函数中的二倍角公式、两角和与差的正余弦公式


本题属于常规问题。第(1)问需要注意三角公式的化简,而第(2)问则需要注意三角函数在定区间上的最值问题。
三、抓住整体,重点突破
我们已经构建了三角恒等变换的公式网络,出于公式的简洁性要求,更是出于角之间相互明了关系的表示,公式里的已知角α,β写成了单角的形式,但这并不意味着具体问题中的角一定就是这样的形式,还要从整体着眼,关注整体间的关系。


四、树立目标,提高效率
解三角恒等变换问题,除要熟悉公式网络以外,还要有强烈的目标意识,在目标的引领下,将已知条件进行转化,逐步推进,直至导出结论。


初次接触本题,大多数考生都会感到无从下手,因为这里的角包含有θ,2θ,4θ,6θ。要想把角都化简为θ,明显工作量太大,毕竟涉及6倍角。可以把目标定位为2θ,这样4θ是2θ的二倍角,6θ是2θ的三倍角,θ是2θ的半角,因此操作起来必然事半功倍。
五、适当推广,提高能力
现在很多考生都要参加学校组织的自主招生考试,自主招生试题比普通高考试题的出题形式更灵活,知识面更广、更深,对考生的能力要求更高。


要求cos(x+y)的值,根据已知条件,只需要平方处理即可;要求sin(x-y)的值,只需要和差化积公式处理即可。
相关文章
- 文科生高考文综高分必备答题公式,史地政三科全!
- 急补物化生!高中各类考试常用[物/化/生]公式汇总!
- 三角函数就考这6个题型,你掌握了吗?
- 熟练解三角形
- “三角函数”的题型只有这6种,最完整的解析过程,老师点头称赞
- 一道得分率很低的数列求和题
- 两角和与差的三角函数
- 全等三角形构造(二):首师大重点班特训题
- 给外甥女的一封信:我是如何学习好数理化的?
- 高中诗歌鉴赏答题公式!满分真的很容易!(内含实用例子)
- 写作|第十三招 并列:多箭指向靶心
- 原创:叙事体任务型材料作文写作指导
- 高中函数、三角、向量阶段复习测验卷(含答案)
- 高中118个三角函数公式,忘记的孩子,默默转了吧……
- 高一 | 当三角形的四心遇上了向量
- 立体几何中的空间向量方法ooo二面角及异面直线的距离
- “平面向量”本领强,沟通代数、几何和三角函数好桥梁!
- 四大满分公式!高考古诗词鉴赏题,名师教你怎么做
- 三角形面积公式盘点,你掌握了几个?
- 最后79天,从300分冲到600分不是梦!行动、方法、状态,你只需
推荐内容
教育新鲜事




 高中丨(高频考点)物理
高中丨(高频考点)物理 期末考试时间定了!收官
期末考试时间定了!收官 高中生逆袭物语:这几步
高中生逆袭物语:这几步 必须收藏!省略句考点全
必须收藏!省略句考点全