三角函数解题中几种错误分析(高3高2)
下面我们从三角函数内容中精选出此类问题的几种解题错误出来,以引起同学们的高度重视!
1.忽视变量的取值范围导致解题错误

此题还有隐含条件没有挖掘出来:
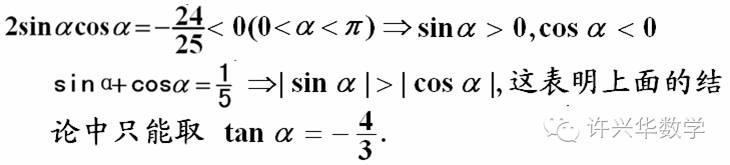
【评注】这类问题的解决首先必须对角α的范围进行讨论,这充分体现了“函数问题,范围优先(尤其是三角函数问题)”的解题基本原则.
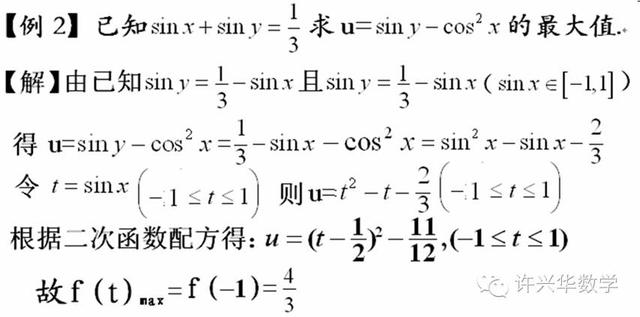
上述解法是错误的。为什么呢?
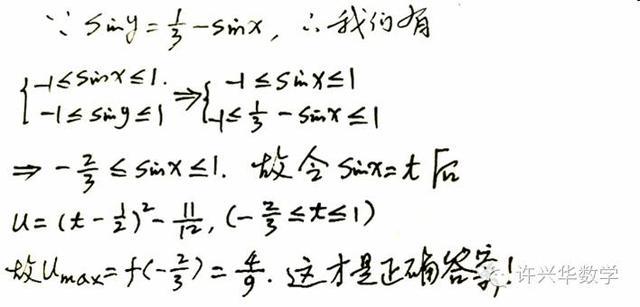

2.忽视了对角的范围的限制导致错误

[错因剖析]没有注意挖掘题目中的隐含条件,忽视了对角的范围的限制,造成出错。

【评注】在已知值求角中,角的范围常常被忽略或不能发现隐含的角的大小关系而出现增根不能排除.要避免上述情况的发生,考生应合理选择三角函数形式进行求解,根据计算结果,估算出角的较精确的取值范围,并不断缩小角的范围,在选择三角函数公式时,一般已知正切函数值,选正切函数,已知正余弦函数值时,选择相应的正余弦函数。如果没有注意挖掘题目中的隐含条件,忽视了对角的范围的限制,这样就容易造成错误。



3.忽视了三角形的性质导致错误

上述解法是错误的。为什么呢?

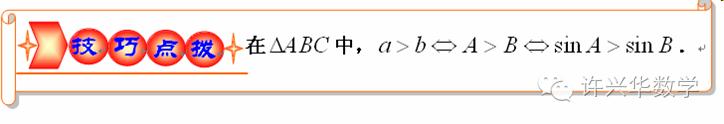


上述解法中(II)的解答是错误的。为什么呢?


【说明】本文只选出三种类型的错误进行分析。由于篇幅所限,没有概括完所有的错误题型。希望此文能给同学们对“三角函数”的学习或复习提供重要的提示作用。
相关文章
- 学生注意!高中不同水平的学生最容易犯这些错误,说得太对了!
- 高三全年重要考试时间表,附各科最易犯的低级错误!一定要记住
- 三角函数就考这6个题型,你掌握了吗?
- 熟练解三角形
- “三角函数”的题型只有这6种,最完整的解析过程,老师点头称赞
- 两角和与差的三角函数
- 全等三角形构造(二):首师大重点班特训题
- 什么样的人最喜欢说“全天下的男人都会犯的错误”
- 写作|第十三招 并列:多箭指向靶心
- 原创:叙事体任务型材料作文写作指导
- 用好错题本高考提20分 教你如何用错题本?
- 高中函数、三角、向量阶段复习测验卷(含答案)
- 高中118个三角函数公式,忘记的孩子,默默转了吧……
- 高一 | 当三角形的四心遇上了向量
- 立体几何中的空间向量方法ooo二面角及异面直线的距离
- “平面向量”本领强,沟通代数、几何和三角函数好桥梁!
- 高三学会这样做错题本,好成绩自然而来!
- 三角形面积公式盘点,你掌握了几个?
- 思维拓展:轻松玩转三道三角函数题
- 高考作文审题立意:稳、准、深、新(1)
推荐内容
教育新鲜事
 高中丨(高频考点)物理
高中丨(高频考点)物理 期末考试时间定了!收官
期末考试时间定了!收官 高中生逆袭物语:这几步
高中生逆袭物语:这几步 必须收藏!省略句考点全
必须收藏!省略句考点全