高二数学考试中导数常见易错考点总结

　　高二数学的第二学期，学生将完成所有基础知识内容的学习。对于绝大多数的理科生而言，这个学期的前半学期学习的是选修2-2这本书，所以很自然的，这本书中的重点--导数将会成为这次期中考试的核心知识点。

　　导数这部分内容对于中学生来说比较抽象，加之新课改更强调数学的工具性，因此很多学生学完导数，对导数的运算法则掌握的比较好--这也是必要的，而对于导数的基本概念、应用中的常见易错点掌握的并不熟练。本文不会面面俱到的讲导数的每种考察方式，而是列举几个学生容易忽略的易错考点，已达到查漏补缺的目的。

　　在历次期中考试中，学生在导数这部分知识常见的易错点包括：

　　一、对导数基本概念的理解。

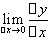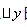　　导数的本质是"平均变化率的极限"，也就是，而这里的形式并不重要，只要是是"相同区间"上的"函数值之差"比上"自变量"之差，就是导数。如果能理解清楚这一点，再看题目常出的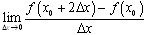、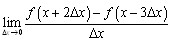之类的形式，就感觉比较清晰了。

　　二、复合函数求导计算错误。

　　对于复合函数求导的规则，同学大多掌握的不错，但题目中真正出现复合函数的时候，计算还是会出问题。问题出在哪，不在于不会算，而是没有发现这是复合函数。

　　课标要求学生掌握形如f(ax+b)的复合函数求导规则，这一点已经限制的很死板了。所以当题目中的函数比较符合这个形式的时候，同学大多也是认的出来的，比如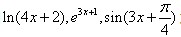这样的函数。反而是内层函数更简单的时候，会被学生忽略，例如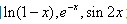这样的函数。所以同学在求导的时候，一定要刻意观察这一点，识别隐蔽在这里的陷阱。

　　三、导数与单调区间的关系。

　　利用导数求函数的的单调区间是导数应用中最基本的题型，按说本不是什么难点。但是这里有一个最大的麻烦，就是导数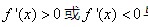与函数的单调性不是充要条件。因此，什么时候写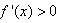，又在什么时候应该写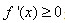是很多同学犯迷糊的地方。

　　这里需要注意一个要点，我们每一步运算或者推导，得到的条件其实都是原条件的必要非充分条件，想清楚这一点，面对这个问题就清晰了。

　　如果原题让我们"求"函数的增区间，我们就用增区间的充分非必要条件，也就是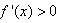来求范围；如果原题给了我们函数增区间的性质，我们就利用增区间的必要非充分条件，也就是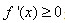来解题。